Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

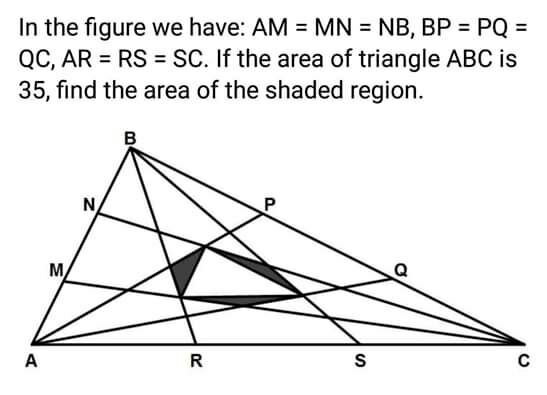
Question Number 84892 by Power last updated on 17/Mar/20

Commented by Power last updated on 17/Mar/20

please see

$$\boldsymbol{\mathrm{please}}\:\boldsymbol{\mathrm{see}} \\ $$

Commented by Power last updated on 17/Mar/20

sir mr W please

$$\boldsymbol{\mathrm{sir}}\:\boldsymbol{\mathrm{mr}}\:\boldsymbol{\mathrm{W}}\:\:\boldsymbol{\mathrm{please}} \\ $$

Commented by Power last updated on 17/Mar/20

sir mind is power pls

$$\mathrm{sir}\:\mathrm{mind}\:\mathrm{is}\:\mathrm{power}\:\mathrm{pls} \\ $$

Commented by Power last updated on 18/Mar/20

solution sir plese

$$\mathrm{solution}\:\mathrm{sir}\:\mathrm{plese} \\ $$

Answered by mr W last updated on 18/Mar/20

Commented by Power last updated on 18/Mar/20

great sir

$$\mathrm{great}\:\mathrm{sir} \\ $$$$ \\ $$

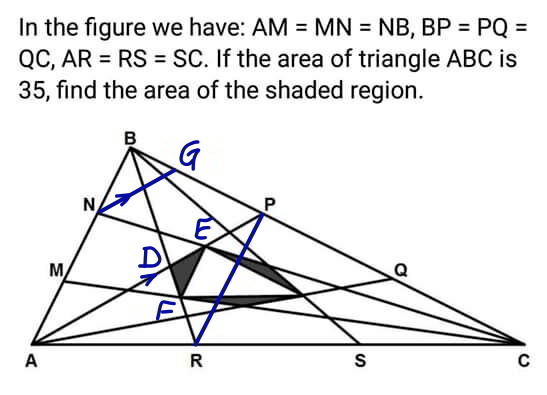
Commented by mr W last updated on 18/Mar/20

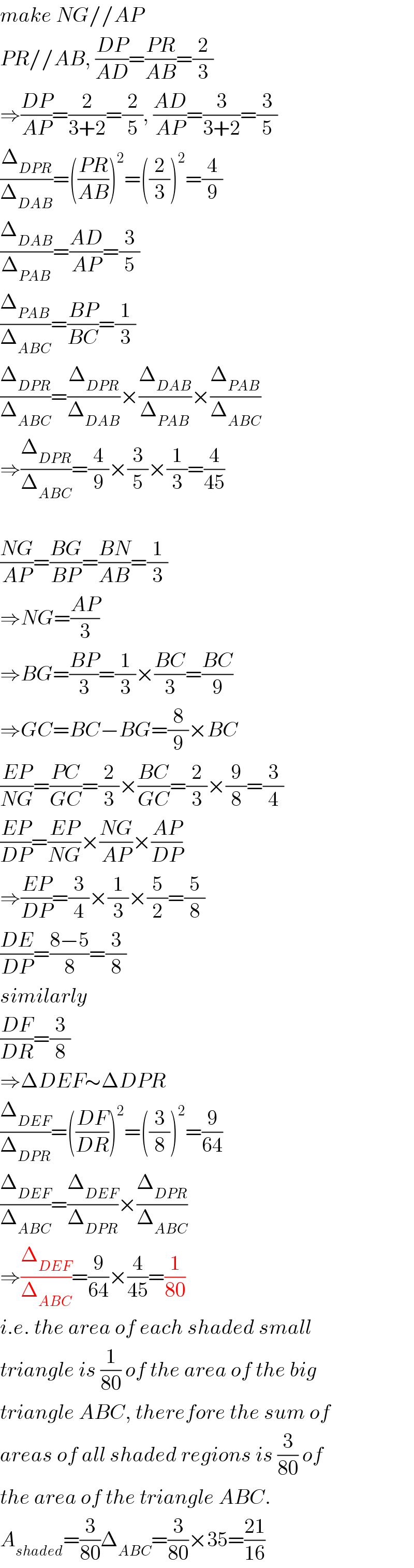
make NG//AP PR//AB, ((DP)/(AD))=((PR)/(AB))=(2/3) ⇒((DP)/(AP))=(2/(3+2))=(2/5), ((AD)/(AP))=(3/(3+2))=(3/5) (Δ_(DPR) /Δ_(DAB) )=(((PR)/(AB)))^2 =((2/3))^2 =(4/9) (Δ_(DAB) /Δ_(PAB) )=((AD)/(AP))=(3/5) (Δ_(PAB) /Δ_(ABC) )=((BP)/(BC))=(1/3) (Δ_(DPR) /Δ_(ABC) )=(Δ_(DPR) /Δ_(DAB) )×(Δ_(DAB) /Δ_(PAB) )×(Δ_(PAB) /Δ_(ABC) ) ⇒(Δ_(DPR) /Δ_(ABC) )=(4/9)×(3/5)×(1/3)=(4/(45)) ((NG)/(AP))=((BG)/(BP))=((BN)/(AB))=(1/3) ⇒NG=((AP)/3) ⇒BG=((BP)/3)=(1/3)×((BC)/3)=((BC)/9) ⇒GC=BC−BG=(8/9)×BC ((EP)/(NG))=((PC)/(GC))=(2/3)×((BC)/(GC))=(2/3)×(9/8)=(3/4) ((EP)/(DP))=((EP)/(NG))×((NG)/(AP))×((AP)/(DP)) ⇒((EP)/(DP))=(3/4)×(1/3)×(5/2)=(5/8) ((DE)/(DP))=((8−5)/8)=(3/8) similarly ((DF)/(DR))=(3/8) ⇒ΔDEF∼ΔDPR (Δ_(DEF) /Δ_(DPR) )=(((DF)/(DR)))^2 =((3/8))^2 =(9/(64)) (Δ_(DEF) /Δ_(ABC) )=(Δ_(DEF) /Δ_(DPR) )×(Δ_(DPR) /Δ_(ABC) ) ⇒(Δ_(DEF) /Δ_(ABC) )=(9/(64))×(4/(45))=(1/(80)) i.e. the area of each shaded small triangle is (1/(80)) of the area of the big triangle ABC, therefore the sum of areas of all shaded regions is (3/(80)) of the area of the triangle ABC. A_(shaded) =(3/(80))Δ_(ABC) =(3/(80))×35=((21)/(16))

$${make}\:{NG}//{AP} \\ $$$${PR}//{AB},\:\frac{{DP}}{{AD}}=\frac{{PR}}{{AB}}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\Rightarrow\frac{{DP}}{{AP}}=\frac{\mathrm{2}}{\mathrm{3}+\mathrm{2}}=\frac{\mathrm{2}}{\mathrm{5}},\:\frac{{AD}}{{AP}}=\frac{\mathrm{3}}{\mathrm{3}+\mathrm{2}}=\frac{\mathrm{3}}{\mathrm{5}} \\ $$$$\frac{\Delta_{{DPR}} }{\Delta_{{DAB}} }=\left(\frac{{PR}}{{AB}}\right)^{\mathrm{2}} =\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{2}} =\frac{\mathrm{4}}{\mathrm{9}} \\ $$$$\frac{\Delta_{{DAB}} }{\Delta_{{PAB}} }=\frac{{AD}}{{AP}}=\frac{\mathrm{3}}{\mathrm{5}} \\ $$$$\frac{\Delta_{{PAB}} }{\Delta_{{ABC}} }=\frac{{BP}}{{BC}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\frac{\Delta_{{DPR}} }{\Delta_{{ABC}} }=\frac{\Delta_{{DPR}} }{\Delta_{{DAB}} }×\frac{\Delta_{{DAB}} }{\Delta_{{PAB}} }×\frac{\Delta_{{PAB}} }{\Delta_{{ABC}} } \\ $$$$\Rightarrow\frac{\Delta_{{DPR}} }{\Delta_{{ABC}} }=\frac{\mathrm{4}}{\mathrm{9}}×\frac{\mathrm{3}}{\mathrm{5}}×\frac{\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{4}}{\mathrm{45}} \\ $$$$ \\ $$$$\frac{{NG}}{{AP}}=\frac{{BG}}{{BP}}=\frac{{BN}}{{AB}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow{NG}=\frac{{AP}}{\mathrm{3}} \\ $$$$\Rightarrow{BG}=\frac{{BP}}{\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{3}}×\frac{{BC}}{\mathrm{3}}=\frac{{BC}}{\mathrm{9}} \\ $$$$\Rightarrow{GC}={BC}−{BG}=\frac{\mathrm{8}}{\mathrm{9}}×{BC} \\ $$$$\frac{{EP}}{{NG}}=\frac{{PC}}{{GC}}=\frac{\mathrm{2}}{\mathrm{3}}×\frac{{BC}}{{GC}}=\frac{\mathrm{2}}{\mathrm{3}}×\frac{\mathrm{9}}{\mathrm{8}}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\frac{{EP}}{{DP}}=\frac{{EP}}{{NG}}×\frac{{NG}}{{AP}}×\frac{{AP}}{{DP}} \\ $$$$\Rightarrow\frac{{EP}}{{DP}}=\frac{\mathrm{3}}{\mathrm{4}}×\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{5}}{\mathrm{2}}=\frac{\mathrm{5}}{\mathrm{8}} \\ $$$$\frac{{DE}}{{DP}}=\frac{\mathrm{8}−\mathrm{5}}{\mathrm{8}}=\frac{\mathrm{3}}{\mathrm{8}} \\ $$$${similarly} \\ $$$$\frac{{DF}}{{DR}}=\frac{\mathrm{3}}{\mathrm{8}} \\ $$$$\Rightarrow\Delta{DEF}\sim\Delta{DPR} \\ $$$$\frac{\Delta_{{DEF}} }{\Delta_{{DPR}} }=\left(\frac{{DF}}{{DR}}\right)^{\mathrm{2}} =\left(\frac{\mathrm{3}}{\mathrm{8}}\right)^{\mathrm{2}} =\frac{\mathrm{9}}{\mathrm{64}} \\ $$$$\frac{\Delta_{{DEF}} }{\Delta_{{ABC}} }=\frac{\Delta_{{DEF}} }{\Delta_{{DPR}} }×\frac{\Delta_{{DPR}} }{\Delta_{{ABC}} } \\ $$$$\Rightarrow\frac{\Delta_{{DEF}} }{\Delta_{{ABC}} }=\frac{\mathrm{9}}{\mathrm{64}}×\frac{\mathrm{4}}{\mathrm{45}}=\frac{\mathrm{1}}{\mathrm{80}} \\ $$$${i}.{e}.\:{the}\:{area}\:{of}\:{each}\:{shaded}\:{small} \\ $$$${triangle}\:{is}\:\frac{\mathrm{1}}{\mathrm{80}}\:{of}\:{the}\:{area}\:{of}\:{the}\:{big} \\ $$$${triangle}\:{ABC},\:{therefore}\:{the}\:{sum}\:{of} \\ $$$${areas}\:{of}\:{all}\:{shaded}\:{regions}\:{is}\:\frac{\mathrm{3}}{\mathrm{80}}\:{of} \\ $$$${the}\:{area}\:{of}\:{the}\:{triangle}\:{ABC}. \\ $$$${A}_{{shaded}} =\frac{\mathrm{3}}{\mathrm{80}}\Delta_{{ABC}} =\frac{\mathrm{3}}{\mathrm{80}}×\mathrm{35}=\frac{\mathrm{21}}{\mathrm{16}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com