Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 84718 by Power last updated on 15/Mar/20

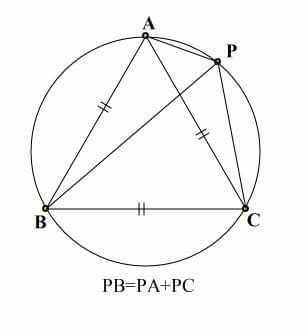
Answered by mr W last updated on 15/Mar/20

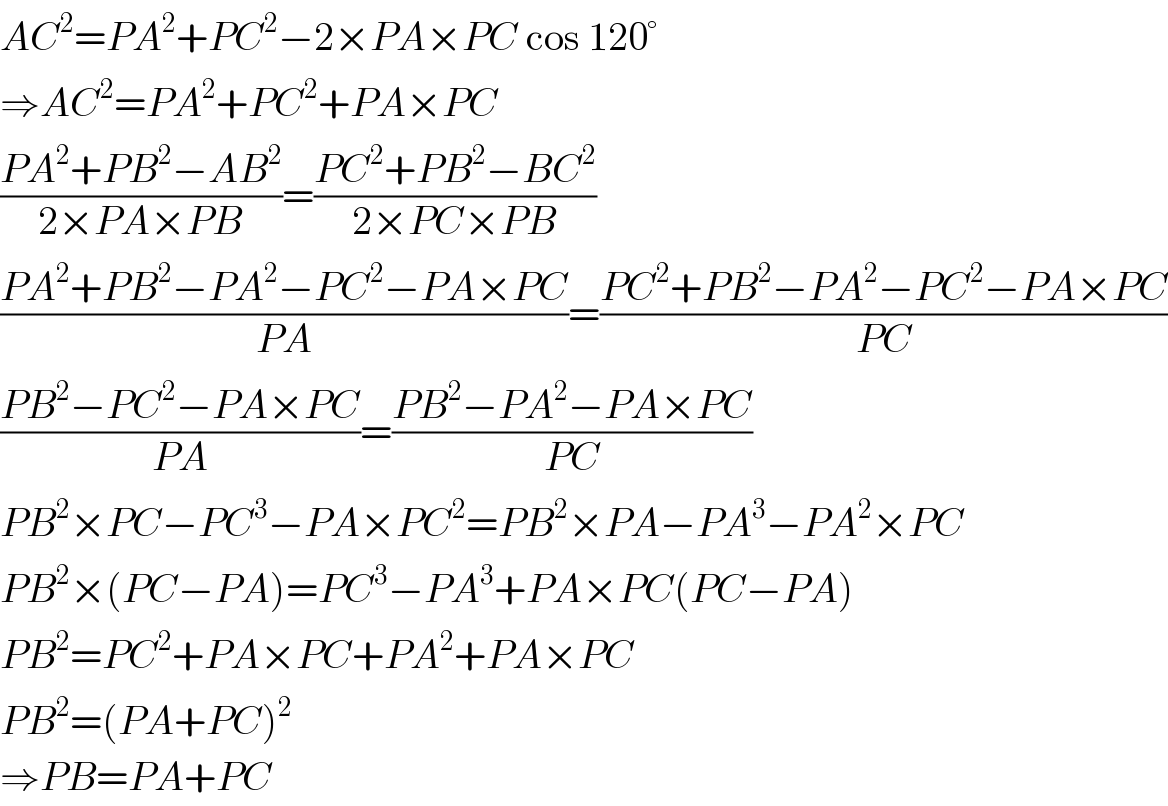
AC^2 =PA^2 +PC^2 −2×PA×PC cos 120° ⇒AC^2 =PA^2 +PC^2 +PA×PC ((PA^2 +PB^2 −AB^2 )/(2×PA×PB))=((PC^2 +PB^2 −BC^2 )/(2×PC×PB)) ((PA^2 +PB^2 −PA^2 −PC^2 −PA×PC)/(PA))=((PC^2 +PB^2 −PA^2 −PC^2 −PA×PC)/(PC)) ((PB^2 −PC^2 −PA×PC)/(PA))=((PB^2 −PA^2 −PA×PC)/(PC)) PB^2 ×PC−PC^3 −PA×PC^2 =PB^2 ×PA−PA^3 −PA^2 ×PC PB^2 ×(PC−PA)=PC^3 −PA^3 +PA×PC(PC−PA) PB^2 =PC^2 +PA×PC+PA^2 +PA×PC PB^2 =(PA+PC)^2 ⇒PB=PA+PC

$${AC}^{\mathrm{2}} ={PA}^{\mathrm{2}} +{PC}^{\mathrm{2}} −\mathrm{2}×{PA}×{PC}\:\mathrm{cos}\:\mathrm{120}° \\ $$$$\Rightarrow{AC}^{\mathrm{2}} ={PA}^{\mathrm{2}} +{PC}^{\mathrm{2}} +{PA}×{PC} \\ $$$$\frac{{PA}^{\mathrm{2}} +{PB}^{\mathrm{2}} −{AB}^{\mathrm{2}} }{\mathrm{2}×{PA}×{PB}}=\frac{{PC}^{\mathrm{2}} +{PB}^{\mathrm{2}} −{BC}^{\mathrm{2}} }{\mathrm{2}×{PC}×{PB}} \\ $$$$\frac{{PA}^{\mathrm{2}} +{PB}^{\mathrm{2}} −{PA}^{\mathrm{2}} −{PC}^{\mathrm{2}} −{PA}×{PC}}{{PA}}=\frac{{PC}^{\mathrm{2}} +{PB}^{\mathrm{2}} −{PA}^{\mathrm{2}} −{PC}^{\mathrm{2}} −{PA}×{PC}}{{PC}} \\ $$$$\frac{{PB}^{\mathrm{2}} −{PC}^{\mathrm{2}} −{PA}×{PC}}{{PA}}=\frac{{PB}^{\mathrm{2}} −{PA}^{\mathrm{2}} −{PA}×{PC}}{{PC}} \\ $$$${PB}^{\mathrm{2}} ×{PC}−{PC}^{\mathrm{3}} −{PA}×{PC}^{\mathrm{2}} ={PB}^{\mathrm{2}} ×{PA}−{PA}^{\mathrm{3}} −{PA}^{\mathrm{2}} ×{PC} \\ $$$${PB}^{\mathrm{2}} ×\left({PC}−{PA}\right)={PC}^{\mathrm{3}} −{PA}^{\mathrm{3}} +{PA}×{PC}\left({PC}−{PA}\right) \\ $$$${PB}^{\mathrm{2}} ={PC}^{\mathrm{2}} +{PA}×{PC}+{PA}^{\mathrm{2}} +{PA}×{PC} \\ $$$${PB}^{\mathrm{2}} =\left({PA}+{PC}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{PB}={PA}+{PC} \\ $$

Commented by Power last updated on 15/Mar/20

thanks

$$\mathrm{thanks} \\ $$

Answered by behi83417@gmail.com last updated on 15/Mar/20

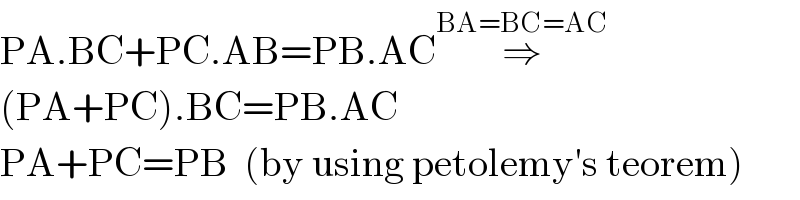
PA.BC+PC.AB=PB.AC⇒^(BA=BC=AC) (PA+PC).BC=PB.AC PA+PC=PB (by using petolemy′s teorem)

$$\mathrm{PA}.\mathrm{BC}+\mathrm{PC}.\mathrm{AB}=\mathrm{PB}.\mathrm{AC}\overset{\mathrm{BA}=\mathrm{BC}=\mathrm{AC}} {\Rightarrow} \\ $$$$\left(\mathrm{PA}+\mathrm{PC}\right).\mathrm{BC}=\mathrm{PB}.\mathrm{AC} \\ $$$$\mathrm{PA}+\mathrm{PC}=\mathrm{PB}\:\:\left(\mathrm{by}\:\mathrm{using}\:\mathrm{petolemy}'\mathrm{s}\:\mathrm{teorem}\right) \\ $$

Commented by mr W last updated on 15/Mar/20

nice way sir!

$${nice}\:{way}\:{sir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com