Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 84708 by Power last updated on 15/Mar/20

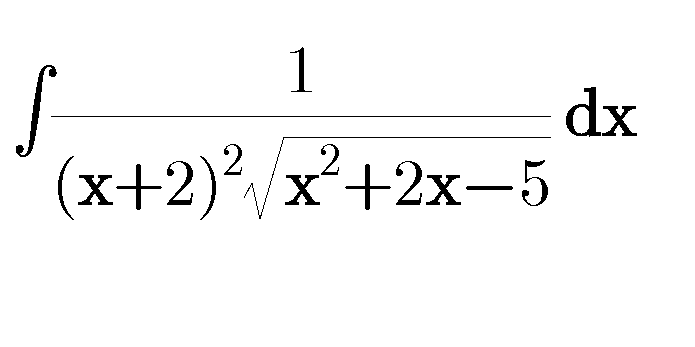
Answered by TANMAY PANACEA last updated on 16/Mar/20

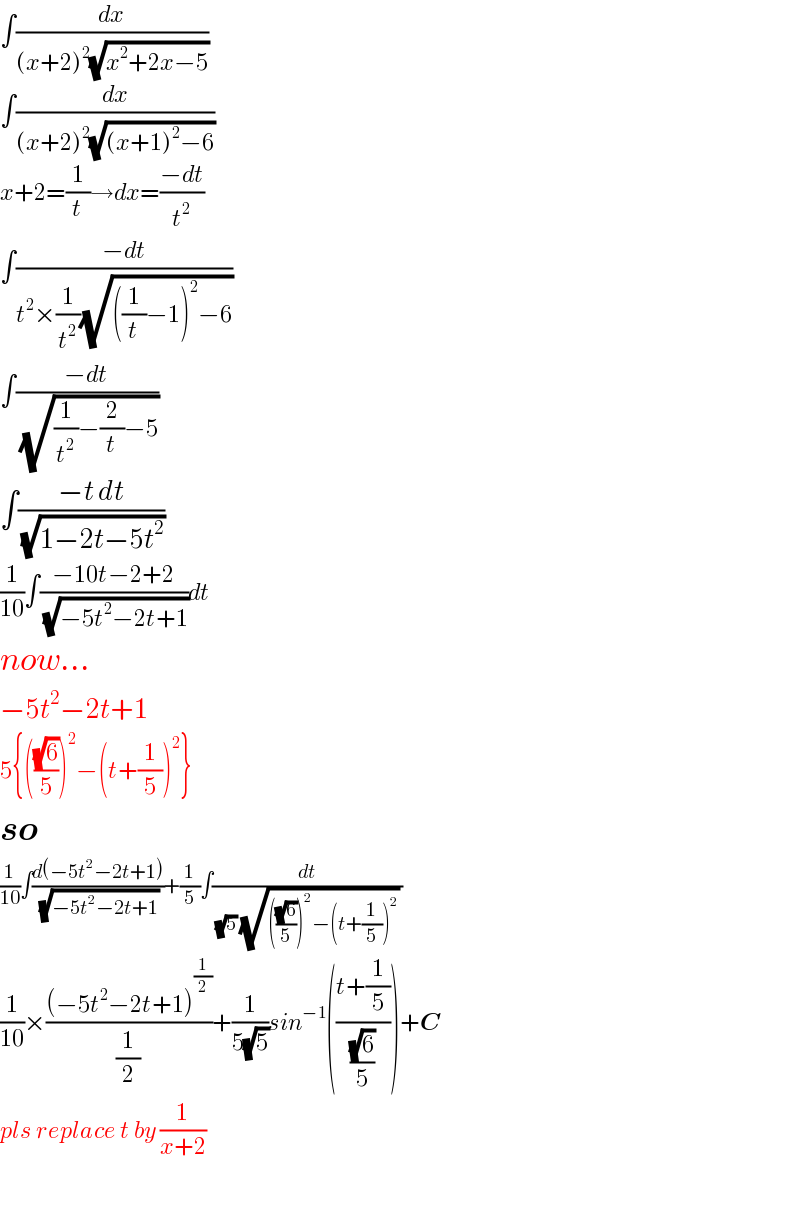
∫(dx/((x+2)^2 (√(x^2 +2x−5)))) ∫(dx/((x+2)^2 (√((x+1)^2 −6)))) x+2=(1/t)→dx=((−dt)/t^2 ) ∫((−dt)/(t^2 ×(1/t^2 )(√(((1/t)−1)^2 −6)))) ∫((−dt)/(√((1/t^2 )−(2/t)−5))) ∫((−t dt)/(√(1−2t−5t^2 ))) (1/(10))∫((−10t−2+2)/(√(−5t^2 −2t+1)))dt now... −5t^2 −2t+1 5{(((√6)/5))^2 −(t+(1/5))^2 } so (1/(10))∫((d(−5t^2 −2t+1))/(√(−5t^2 −2t+1)))+(1/5)∫(dt/((√5) (√((((√6)/5))^2 −(t+(1/5))^2 )) )) (1/(10))×(((−5t^2 −2t+1)^(1/2) )/(1/2))+(1/(5(√5)))sin^(−1) (((t+(1/5))/((√6)/5)))+C pls replace t by (1/(x+2))

$$\int\frac{{dx}}{\left({x}+\mathrm{2}\right)^{\mathrm{2}} \sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{5}}} \\ $$$$\int\frac{{dx}}{\left({x}+\mathrm{2}\right)^{\mathrm{2}} \sqrt{\left({x}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{6}}} \\ $$$${x}+\mathrm{2}=\frac{\mathrm{1}}{{t}}\rightarrow{dx}=\frac{−{dt}}{{t}^{\mathrm{2}} } \\ $$$$\int\frac{−{dt}}{{t}^{\mathrm{2}} ×\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\sqrt{\left(\frac{\mathrm{1}}{{t}}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{6}}} \\ $$$$\int\frac{−{dt}}{\sqrt{\frac{\mathrm{1}}{{t}^{\mathrm{2}} }−\frac{\mathrm{2}}{{t}}−\mathrm{5}}} \\ $$$$\int\frac{−{t}\:{dt}}{\sqrt{\mathrm{1}−\mathrm{2}{t}−\mathrm{5}{t}^{\mathrm{2}} }} \\ $$$$\frac{\mathrm{1}}{\mathrm{10}}\int\frac{−\mathrm{10}{t}−\mathrm{2}+\mathrm{2}}{\sqrt{−\mathrm{5}{t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{1}}}{dt} \\ $$$${now}... \\ $$$$−\mathrm{5}{t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{1} \\ $$$$\mathrm{5}\left\{\left(\frac{\sqrt{\mathrm{6}}}{\mathrm{5}}\right)^{\mathrm{2}} −\left({t}+\frac{\mathrm{1}}{\mathrm{5}}\right)^{\mathrm{2}} \right\} \\ $$$$\boldsymbol{{so}} \\ $$$$\frac{\mathrm{1}}{\mathrm{10}}\int\frac{{d}\left(−\mathrm{5}{t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{1}\right)}{\sqrt{−\mathrm{5}{t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{1}}}+\frac{\mathrm{1}}{\mathrm{5}}\int\frac{{dt}}{\sqrt{\mathrm{5}}\:\sqrt{\left(\frac{\sqrt{\mathrm{6}}}{\mathrm{5}}\right)^{\mathrm{2}} −\left({t}+\frac{\mathrm{1}}{\mathrm{5}}\right)^{\mathrm{2}} }\:} \\ $$$$\frac{\mathrm{1}}{\mathrm{10}}×\frac{\left(−\mathrm{5}{t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} }{\frac{\mathrm{1}}{\mathrm{2}}}+\frac{\mathrm{1}}{\mathrm{5}\sqrt{\mathrm{5}}}{sin}^{−\mathrm{1}} \left(\frac{{t}+\frac{\mathrm{1}}{\mathrm{5}}}{\frac{\sqrt{\mathrm{6}}}{\mathrm{5}}}\right)+\boldsymbol{{C}} \\ $$$${pls}\:{replace}\:{t}\:{by}\:\frac{\mathrm{1}}{{x}+\mathrm{2}} \\ $$$$ \\ $$

Commented by Power last updated on 15/Mar/20

thanks

$$\mathrm{thanks} \\ $$

Commented by TANMAY PANACEA last updated on 15/Mar/20

most welcome

$${most}\:{welcome} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com