
Question Number 84655 by ajfour last updated on 14/Mar/20
Commented by ajfour last updated on 14/Mar/20

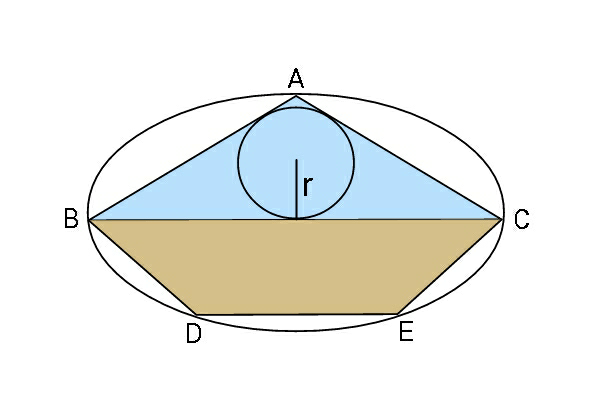
$${If}\:{area}\:{of}\:\bigtriangleup{ABC}\:\:{is}\:{equal}\:{to} \\ $$$${max}\:{trapezium}\:{area}\:{BCED}\:, \\ $$$${find}\:{r}\:{in}\:{terms}\:{of}\:{ellipse}\: \\ $$$${parameters}\:{a}\:{and}\:{b}. \\ $$
Answered by mr W last updated on 15/Mar/20
Commented by mr W last updated on 15/Mar/20
![let α=cos^(−1) (h/b) BC=2a sin α [BCED]_(max) =((ab)/2)[3 sin (((2α)/3))−sin (2α)] [ABC]=a(b+h) sin α ((ab)/2)[3 sin (((2α)/3))−sin (2α)]=a(b+h) sin α 3 sin (((2α)/3))−sin (2α)=2(1+(h/b)) sin α let λ=(h/b) ⇒α=cos^(−1) λ ⇒3 sin (((2α)/3))=2(2λ+1) sin α ⇒λ≈0.121555 AC=(√(a^2 (1−λ^2 )+b^2 (1+λ)^2 )) ab(1+λ) sin α=r(a sin α+(√(a^2 (1−λ^2 )+b^2 (1+λ)^2 )) b(1+λ)=r[1+(√(1+(((1+λ)b^2 )/((1−λ)a^2 ))))] ⇒(r/b)=((1+λ)/(1+(√(1+(((1+λ)b^2 )/((1−λ)a^2 )))))) examples: (b/a)=1 ⇒(r/b)=0.447032 (b/a)=(2/3) ⇒(r/b)=0.498031 (b/a)=(1/2) ⇒(r/b)=0.522003 (b/a)=2 ⇒(r/b)=0.323100](Q84687.png)
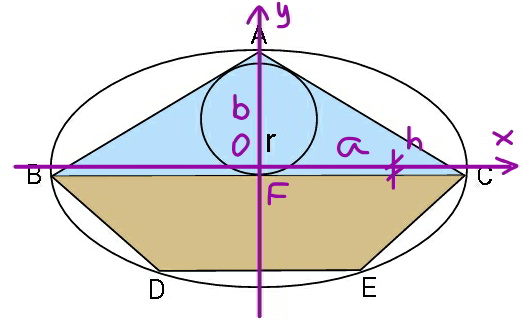
$${let}\:\alpha=\mathrm{cos}^{−\mathrm{1}} \frac{{h}}{{b}} \\ $$$${BC}=\mathrm{2}{a}\:\mathrm{sin}\:\alpha \\ $$$$\left[{BCED}\right]_{{max}} =\frac{{ab}}{\mathrm{2}}\left[\mathrm{3}\:\mathrm{sin}\:\left(\frac{\mathrm{2}\alpha}{\mathrm{3}}\right)−\mathrm{sin}\:\left(\mathrm{2}\alpha\right)\right] \\ $$$$\left[{ABC}\right]={a}\left({b}+{h}\right)\:\mathrm{sin}\:\alpha \\ $$$$\frac{{ab}}{\mathrm{2}}\left[\mathrm{3}\:\mathrm{sin}\:\left(\frac{\mathrm{2}\alpha}{\mathrm{3}}\right)−\mathrm{sin}\:\left(\mathrm{2}\alpha\right)\right]={a}\left({b}+{h}\right)\:\mathrm{sin}\:\alpha \\ $$$$\mathrm{3}\:\mathrm{sin}\:\left(\frac{\mathrm{2}\alpha}{\mathrm{3}}\right)−\mathrm{sin}\:\left(\mathrm{2}\alpha\right)=\mathrm{2}\left(\mathrm{1}+\frac{{h}}{{b}}\right)\:\mathrm{sin}\:\alpha \\ $$$${let}\:\lambda=\frac{{h}}{{b}} \\ $$$$\Rightarrow\alpha=\mathrm{cos}^{−\mathrm{1}} \lambda \\ $$$$\Rightarrow\mathrm{3}\:\mathrm{sin}\:\left(\frac{\mathrm{2}\alpha}{\mathrm{3}}\right)=\mathrm{2}\left(\mathrm{2}\lambda+\mathrm{1}\right)\:\mathrm{sin}\:\alpha \\ $$$$\Rightarrow\lambda\approx\mathrm{0}.\mathrm{121555} \\ $$$$ \\ $$$${AC}=\sqrt{{a}^{\mathrm{2}} \left(\mathrm{1}−\lambda^{\mathrm{2}} \right)+{b}^{\mathrm{2}} \left(\mathrm{1}+\lambda\right)^{\mathrm{2}} } \\ $$$${ab}\left(\mathrm{1}+\lambda\right)\:\mathrm{sin}\:\alpha={r}\left({a}\:\mathrm{sin}\:\alpha+\sqrt{{a}^{\mathrm{2}} \left(\mathrm{1}−\lambda^{\mathrm{2}} \right)+{b}^{\mathrm{2}} \left(\mathrm{1}+\lambda\right)^{\mathrm{2}} }\right. \\ $$$${b}\left(\mathrm{1}+\lambda\right)={r}\left[\mathrm{1}+\sqrt{\mathrm{1}+\frac{\left(\mathrm{1}+\lambda\right){b}^{\mathrm{2}} }{\left(\mathrm{1}−\lambda\right){a}^{\mathrm{2}} }}\right] \\ $$$$\Rightarrow\frac{{r}}{{b}}=\frac{\mathrm{1}+\lambda}{\mathrm{1}+\sqrt{\mathrm{1}+\frac{\left(\mathrm{1}+\lambda\right){b}^{\mathrm{2}} }{\left(\mathrm{1}−\lambda\right){a}^{\mathrm{2}} }}} \\ $$$${examples}: \\ $$$$\frac{{b}}{{a}}=\mathrm{1}\:\Rightarrow\frac{{r}}{{b}}=\mathrm{0}.\mathrm{447032} \\ $$$$\frac{{b}}{{a}}=\frac{\mathrm{2}}{\mathrm{3}}\:\Rightarrow\frac{{r}}{{b}}=\mathrm{0}.\mathrm{498031} \\ $$$$\frac{{b}}{{a}}=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\frac{{r}}{{b}}=\mathrm{0}.\mathrm{522003} \\ $$$$\frac{{b}}{{a}}=\mathrm{2}\:\Rightarrow\frac{{r}}{{b}}=\mathrm{0}.\mathrm{323100} \\ $$
Commented by ajfour last updated on 15/Mar/20
![Sir i couldn′t get your logic for [BCED]_(max) , kindly enlighten..](Q84734.png)
$${Sir}\:{i}\:{couldn}'{t}\:{get}\:{your}\:{logic}\:{for} \\ $$$$\left[{BCED}\right]_{{max}} \:,\:{kindly}\:{enlighten}.. \\ $$
Commented by mr W last updated on 15/Mar/20
Commented by mr W last updated on 15/Mar/20
![when wir shrink the ellipse in x− direction in ratio (b/a) to a circle, the ratio of the areas from the triangle ABC to trapezium BCED remains unchanged, i.e. (([ABC])/([BCED]))=(([AB′C′])/([B′C′E′D′])) for the circle with radius b, the trapezium B′C′E′D′ is maximum, when B′D′=D′E′=E′C′ (proof omitted). cos α=(h/b) ⇒α=cos^(−1) (h/b) β=((2α)/3) [B′C′E′D′]_(max) =3×((b^2 sin β)/2)−((b^2 sin 2α)/2) =(b^2 /2)[3 sin (((2α)/3))−sin 2α] [BCED]_(max) =(a/b)×[B′C′E′D′]_(max) =((ab)/2)(3 sin (((2α)/3))−sin 2α) B′C′=2b sin α BC=(a/b)×B′C′=2a sin α](Q84742.png)
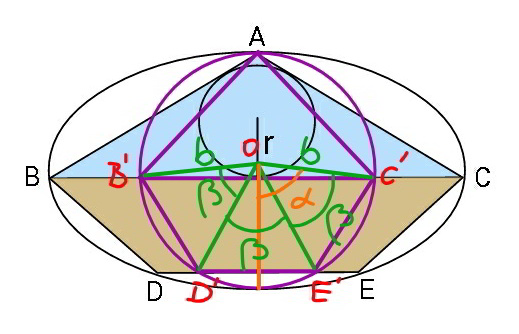
$${when}\:{wir}\:{shrink}\:{the}\:{ellipse}\:{in}\:{x}− \\ $$$${direction}\:{in}\:{ratio}\:\frac{{b}}{{a}}\:{to}\:{a}\:{circle},\:{the} \\ $$$${ratio}\:{of}\:{the}\:{areas}\:{from}\:{the}\:{triangle} \\ $$$${ABC}\:{to}\:{trapezium}\:{BCED}\:{remains} \\ $$$${unchanged},\:{i}.{e}. \\ $$$$\frac{\left[{ABC}\right]}{\left[{BCED}\right]}=\frac{\left[{AB}'{C}'\right]}{\left[{B}'{C}'{E}'{D}'\right]} \\ $$$${for}\:{the}\:{circle}\:{with}\:{radius}\:{b},\:{the} \\ $$$${trapezium}\:{B}'{C}'{E}'{D}'\:{is}\:{maximum}, \\ $$$${when}\:{B}'{D}'={D}'{E}'={E}'{C}'\:\left({proof}\:{omitted}\right). \\ $$$$ \\ $$$$\mathrm{cos}\:\alpha=\frac{{h}}{{b}}\:\Rightarrow\alpha=\mathrm{cos}^{−\mathrm{1}} \frac{{h}}{{b}} \\ $$$$\beta=\frac{\mathrm{2}\alpha}{\mathrm{3}} \\ $$$$\left[{B}'{C}'{E}'{D}'\right]_{{max}} =\mathrm{3}×\frac{{b}^{\mathrm{2}} \:\mathrm{sin}\:\beta}{\mathrm{2}}−\frac{{b}^{\mathrm{2}} \:\mathrm{sin}\:\mathrm{2}\alpha}{\mathrm{2}} \\ $$$$=\frac{{b}^{\mathrm{2}} }{\mathrm{2}}\left[\mathrm{3}\:\mathrm{sin}\:\left(\frac{\mathrm{2}\alpha}{\mathrm{3}}\right)−\mathrm{sin}\:\mathrm{2}\alpha\right] \\ $$$$\left[{BCED}\right]_{{max}} =\frac{{a}}{{b}}×\left[{B}'{C}'{E}'{D}'\right]_{{max}} \\ $$$$=\frac{{ab}}{\mathrm{2}}\left(\mathrm{3}\:\mathrm{sin}\:\left(\frac{\mathrm{2}\alpha}{\mathrm{3}}\right)−\mathrm{sin}\:\mathrm{2}\alpha\right) \\ $$$$ \\ $$$${B}'{C}'=\mathrm{2}{b}\:\mathrm{sin}\:\alpha \\ $$$${BC}=\frac{{a}}{{b}}×{B}'{C}'=\mathrm{2}{a}\:\mathrm{sin}\:\alpha \\ $$
Commented by ajfour last updated on 15/Mar/20

$${Thanks}\:{sir}\:{for}\:{the}\:{explanation}, \\ $$$${i}\:{shall}\:{be}\:{thoroughly}\:{through}\:{it} \\ $$$${by}\:{tomorrow}.. \\ $$
Answered by ajfour last updated on 15/Mar/20
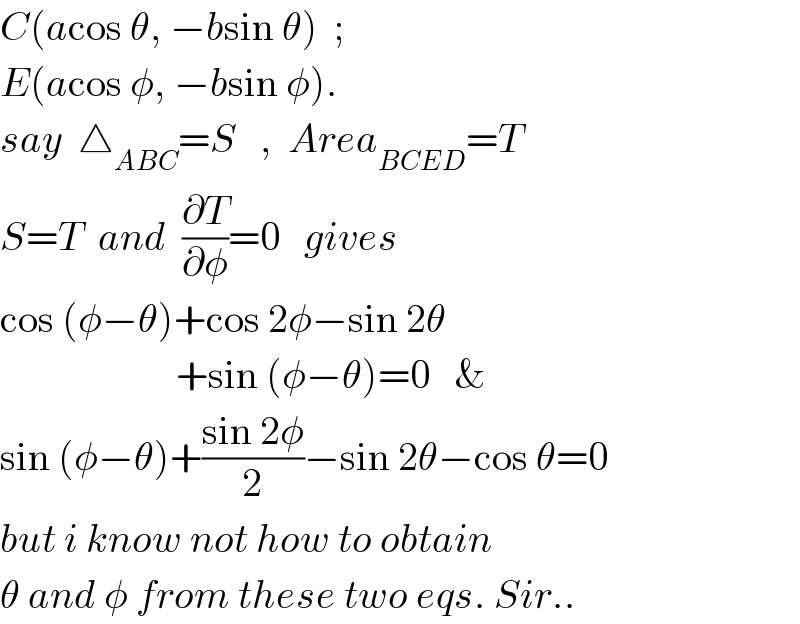
$${C}\left({a}\mathrm{cos}\:\theta,\:−{b}\mathrm{sin}\:\theta\right)\:\:;\: \\ $$$${E}\left({a}\mathrm{cos}\:\phi,\:−{b}\mathrm{sin}\:\phi\right). \\ $$$${say}\:\:\bigtriangleup_{{ABC}} ={S}\:\:\:,\:\:{Area}_{{BCED}} ={T} \\ $$$${S}={T}\:\:{and}\:\:\frac{\partial{T}}{\partial\phi}=\mathrm{0}\:\:\:{gives} \\ $$$$\mathrm{cos}\:\left(\phi−\theta\right)+\mathrm{cos}\:\mathrm{2}\phi−\mathrm{sin}\:\mathrm{2}\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{sin}\:\left(\phi−\theta\right)=\mathrm{0}\:\:\:\& \\ $$$$\mathrm{sin}\:\left(\phi−\theta\right)+\frac{\mathrm{sin}\:\mathrm{2}\phi}{\mathrm{2}}−\mathrm{sin}\:\mathrm{2}\theta−\mathrm{cos}\:\theta=\mathrm{0} \\ $$$${but}\:{i}\:{know}\:{not}\:{how}\:{to}\:{obtain} \\ $$$$\theta\:{and}\:\phi\:{from}\:{these}\:{two}\:{eqs}.\:{Sir}.. \\ $$
Commented by mr W last updated on 16/Mar/20

$${A}={ab}\:\mathrm{cos}\:\theta\:\left(\mathrm{1}+\mathrm{sin}\:\theta\right) \\ $$$${S}={ab}\left(\mathrm{cos}\:\theta+\mathrm{cos}\:\phi\right)\left(\mathrm{sin}\:\phi−\mathrm{sin}\:\theta\right) \\ $$$$ \\ $$$$\frac{{dS}}{{d}\phi}=\mathrm{0} \\ $$$$\left(\mathrm{cos}\:\theta+\mathrm{cos}\:\phi\right)\mathrm{cos}\:\phi−\mathrm{sin}\:\phi\:\left(\mathrm{sin}\:\phi−\mathrm{sin}\:\theta\right)=\mathrm{0} \\ $$$$\mathrm{cos}\:\theta\:\mathrm{cos}\:\phi+\mathrm{cos}^{\mathrm{2}} \:\phi+\mathrm{sin}\:\phi\:\mathrm{sin}\:\theta−\mathrm{sin}^{\mathrm{2}} \:\phi=\mathrm{0} \\ $$$$\Rightarrow\mathrm{cos}\:\left(\phi−\theta\right)+\mathrm{cos}\:\mathrm{2}\phi=\mathrm{0} \\ $$$$\Rightarrow\phi−\theta+\mathrm{2}\phi=\pi \\ $$$$\Rightarrow\phi=\frac{\pi+\theta}{\mathrm{3}} \\ $$$$ \\ $$$${A}={S} \\ $$$$\mathrm{cos}\:\theta\:\left(\mathrm{1}+\mathrm{sin}\:\theta\right)=\left(\mathrm{cos}\:\theta+\mathrm{cos}\:\phi\right)\left(\mathrm{sin}\:\phi−\mathrm{sin}\:\theta\right) \\ $$$$\mathrm{cos}\:\theta+\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta=\mathrm{sin}\:\phi\:\mathrm{cos}\:\theta+\mathrm{cos}\:\phi\:\mathrm{sin}\:\phi−\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta−\mathrm{cos}\:\phi\:\mathrm{sin}\:\theta \\ $$$$\mathrm{sin}\:\left(\phi−\theta\right)+\frac{\mathrm{sin}\:\mathrm{2}\phi}{\mathrm{2}}−\mathrm{sin}\:\mathrm{2}\theta−\mathrm{cos}\:\theta=\mathrm{0} \\ $$$$\mathrm{sin}\:\left(\frac{\pi−\mathrm{2}\theta}{\mathrm{3}}\right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\left(\frac{\mathrm{2}\pi+\mathrm{2}\theta}{\mathrm{3}}\right)−\mathrm{sin}\:\mathrm{2}\theta−\mathrm{cos}\:\theta=\mathrm{0} \\ $$$$\Rightarrow\frac{\mathrm{3}}{\mathrm{2}}\mathrm{sin}\:\left(\frac{\pi−\mathrm{2}\theta}{\mathrm{3}}\right)−\mathrm{sin}\:\mathrm{2}\theta−\mathrm{cos}\:\theta=\mathrm{0} \\ $$$$\Rightarrow\theta\approx\mathrm{6}.\mathrm{981874}° \\ $$$$\Rightarrow\frac{{h}}{{b}}=\mathrm{sin}\:\theta\approx\mathrm{0}.\mathrm{121555}\:\:\left(=\lambda\right) \\ $$
Commented by mr W last updated on 16/Mar/20
$${the}\:{result}\:{is}\:{the}\:{same}\:{as}\:{mine}. \\ $$
Commented by ajfour last updated on 16/Mar/20
$${Thank}\:{you}\:{sir},\:{beautifully} \\ $$$${handled}! \\ $$
