Question Number 84628 by mr W last updated on 14/Mar/20
Commented by mr W last updated on 14/Mar/20

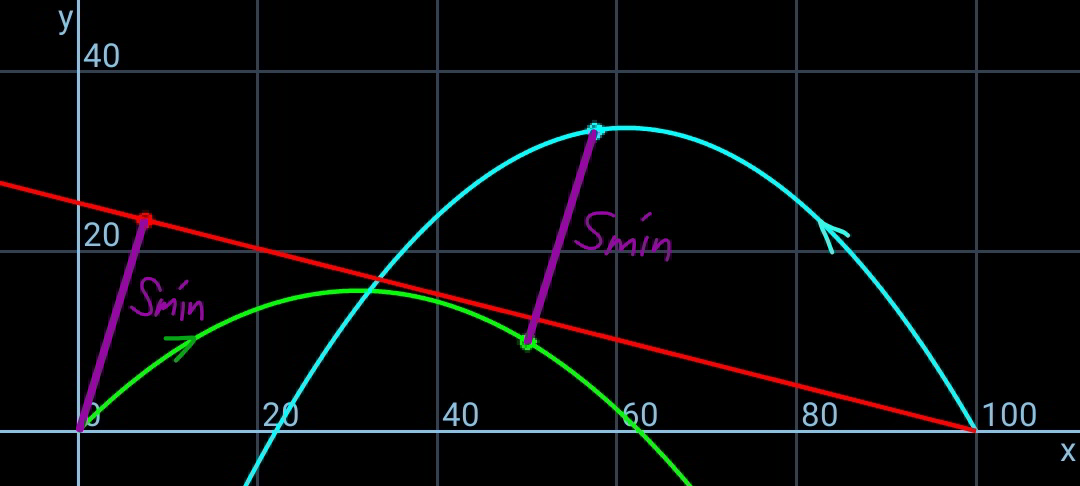
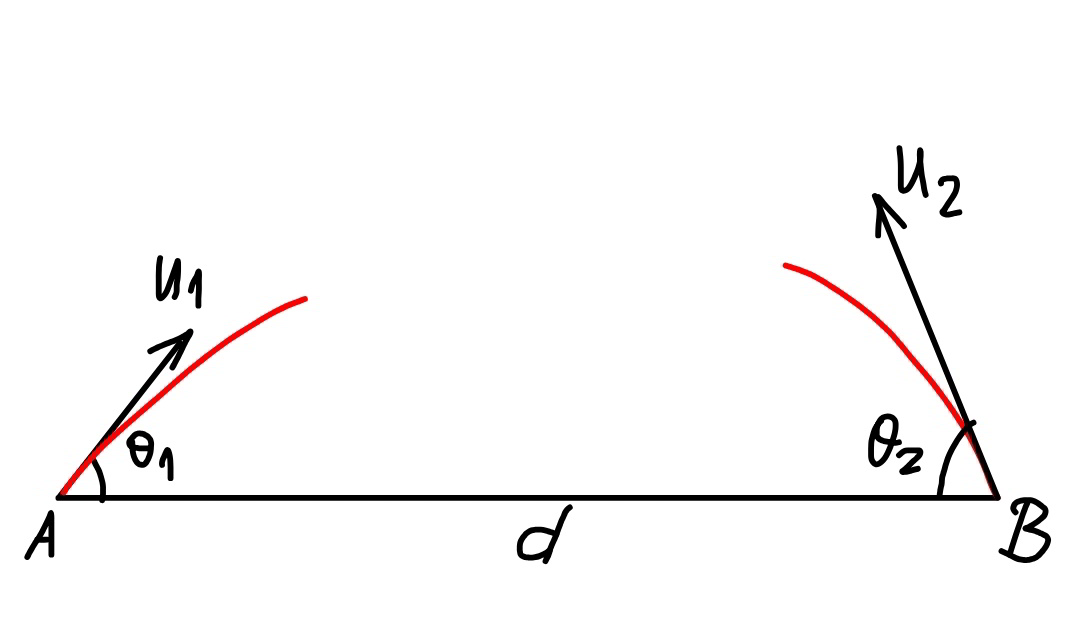
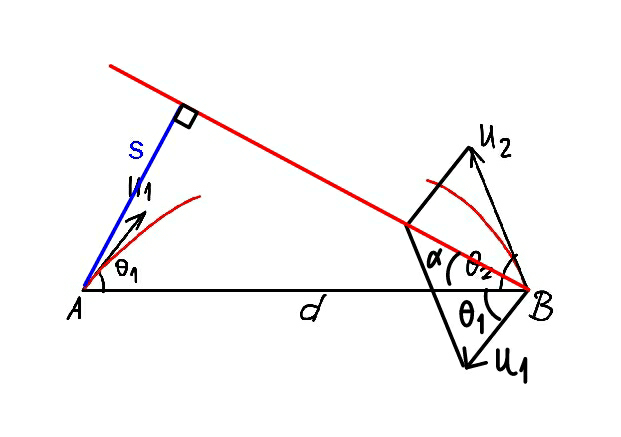
$${The}\:{distance}\:{between}\:{A}\:{and}\:{B}\:{is}\:{d}. \\ $$$${Two}\:{projectiles}\:{are}\:{shot}\:{at}\:{the}\:{same} \\ $$$${time}\:{as}\:{shown}. \\ $$$${After}\:{which}\:{time}\:{are}\:{the}\:{projectiles} \\ $$$${closest}\:{to}\:{each}\:{other}?\:{Find}\:{this}\: \\ $$$${smallest}\:{distance}\:{between}\:{them}. \\ $$
Answered by ajfour last updated on 14/Mar/20
Commented by ajfour last updated on 14/Mar/20
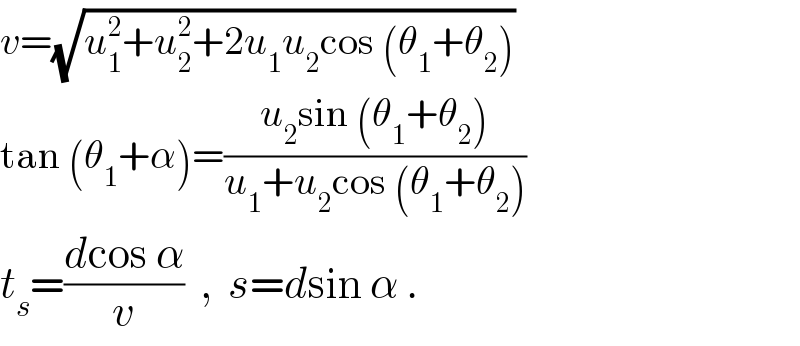
$${v}=\sqrt{{u}_{\mathrm{1}} ^{\mathrm{2}} +{u}_{\mathrm{2}} ^{\mathrm{2}} +\mathrm{2}{u}_{\mathrm{1}} {u}_{\mathrm{2}} \mathrm{cos}\:\left(\theta_{\mathrm{1}} +\theta_{\mathrm{2}} \right)} \\ $$$$\mathrm{tan}\:\left(\theta_{\mathrm{1}} +\alpha\right)=\frac{{u}_{\mathrm{2}} \mathrm{sin}\:\left(\theta_{\mathrm{1}} +\theta_{\mathrm{2}} \right)}{{u}_{\mathrm{1}} +{u}_{\mathrm{2}} \mathrm{cos}\:\left(\theta_{\mathrm{1}} +\theta_{\mathrm{2}} \right)} \\ $$$${t}_{{s}} =\frac{{d}\mathrm{cos}\:\alpha}{{v}}\:\:,\:\:{s}={d}\mathrm{sin}\:\alpha\:. \\ $$
Commented by mr W last updated on 14/Mar/20

$${perfect}\:{sir}! \\ $$
Commented by mr W last updated on 14/Mar/20