Question and Answers Forum

All Questions      Topic List

Coordinate Geometry Questions

Previous in All Question      Next in All Question      

Previous in Coordinate Geometry      Next in Coordinate Geometry      

Question Number 84441 by Power last updated on 13/Mar/20

Commented by Power last updated on 13/Mar/20

sir please solution

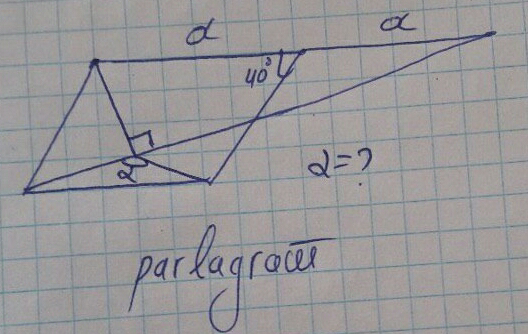
$$\mathrm{sir}\:\mathrm{please}\:\mathrm{solution} \\ $$

Answered by mr W last updated on 13/Mar/20

Commented by mr W last updated on 13/Mar/20

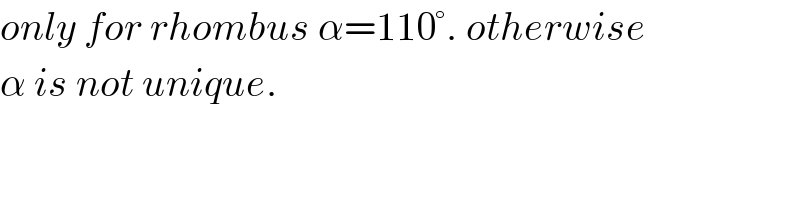
only for rhombus α=110°. otherwise α is not unique.

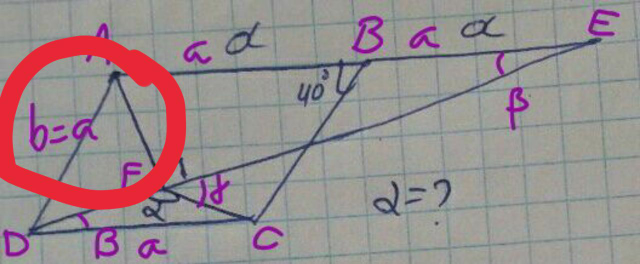
$${only}\:{for}\:{rhombus}\:\alpha=\mathrm{110}°.\:{otherwise} \\ $$$$\alpha\:{is}\:{not}\:{unique}. \\ $$

Commented by mr W last updated on 13/Mar/20

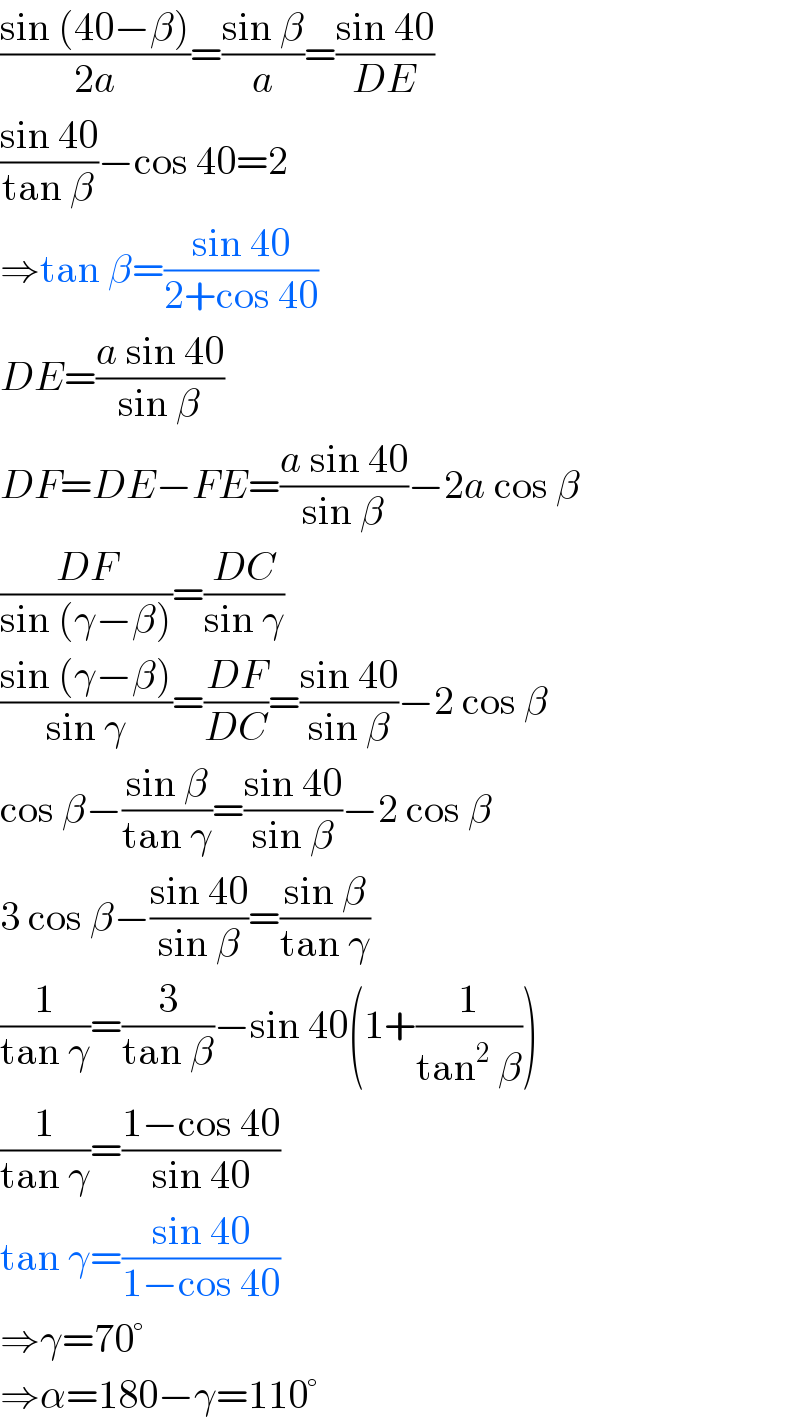
((sin (40−β))/(2a))=((sin β)/a)=((sin 40)/(DE)) ((sin 40)/(tan β))−cos 40=2 ⇒tan β=((sin 40)/(2+cos 40)) DE=((a sin 40)/(sin β)) DF=DE−FE=((a sin 40)/(sin β))−2a cos β ((DF)/(sin (γ−β)))=((DC)/(sin γ)) ((sin (γ−β))/(sin γ))=((DF)/(DC))=((sin 40)/(sin β))−2 cos β cos β−((sin β)/(tan γ))=((sin 40)/(sin β))−2 cos β 3 cos β−((sin 40)/(sin β))=((sin β)/(tan γ)) (1/(tan γ))=(3/(tan β))−sin 40(1+(1/(tan^2 β))) (1/(tan γ))=((1−cos 40)/(sin 40)) tan γ=((sin 40)/(1−cos 40)) ⇒γ=70° ⇒α=180−γ=110°

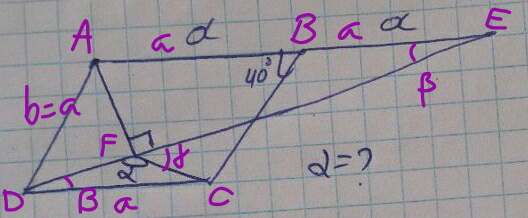
$$\frac{\mathrm{sin}\:\left(\mathrm{40}−\beta\right)}{\mathrm{2}{a}}=\frac{\mathrm{sin}\:\beta}{{a}}=\frac{\mathrm{sin}\:\mathrm{40}}{{DE}} \\ $$$$\frac{\mathrm{sin}\:\mathrm{40}}{\mathrm{tan}\:\beta}−\mathrm{cos}\:\mathrm{40}=\mathrm{2} \\ $$$$\Rightarrow\mathrm{tan}\:\beta=\frac{\mathrm{sin}\:\mathrm{40}}{\mathrm{2}+\mathrm{cos}\:\mathrm{40}} \\ $$$${DE}=\frac{{a}\:\mathrm{sin}\:\mathrm{40}}{\mathrm{sin}\:\beta} \\ $$$${DF}={DE}−{FE}=\frac{{a}\:\mathrm{sin}\:\mathrm{40}}{\mathrm{sin}\:\beta}−\mathrm{2}{a}\:\mathrm{cos}\:\beta \\ $$$$\frac{{DF}}{\mathrm{sin}\:\left(\gamma−\beta\right)}=\frac{{DC}}{\mathrm{sin}\:\gamma} \\ $$$$\frac{\mathrm{sin}\:\left(\gamma−\beta\right)}{\mathrm{sin}\:\gamma}=\frac{{DF}}{{DC}}=\frac{\mathrm{sin}\:\mathrm{40}}{\mathrm{sin}\:\beta}−\mathrm{2}\:\mathrm{cos}\:\beta \\ $$$$\mathrm{cos}\:\beta−\frac{\mathrm{sin}\:\beta}{\mathrm{tan}\:\gamma}=\frac{\mathrm{sin}\:\mathrm{40}}{\mathrm{sin}\:\beta}−\mathrm{2}\:\mathrm{cos}\:\beta \\ $$$$\mathrm{3}\:\mathrm{cos}\:\beta−\frac{\mathrm{sin}\:\mathrm{40}}{\mathrm{sin}\:\beta}=\frac{\mathrm{sin}\:\beta}{\mathrm{tan}\:\gamma} \\ $$$$\frac{\mathrm{1}}{\mathrm{tan}\:\gamma}=\frac{\mathrm{3}}{\mathrm{tan}\:\beta}−\mathrm{sin}\:\mathrm{40}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{tan}^{\mathrm{2}} \:\beta}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{tan}\:\gamma}=\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{40}}{\mathrm{sin}\:\mathrm{40}} \\ $$$$\mathrm{tan}\:\gamma=\frac{\mathrm{sin}\:\mathrm{40}}{\mathrm{1}−\mathrm{cos}\:\mathrm{40}} \\ $$$$\Rightarrow\gamma=\mathrm{70}° \\ $$$$\Rightarrow\alpha=\mathrm{180}−\gamma=\mathrm{110}° \\ $$

Commented by Power last updated on 13/Mar/20

thank you sir

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by Power last updated on 13/Mar/20

Commented by Power last updated on 13/Mar/20

romb ?

$$\mathrm{romb}\:? \\ $$

Commented by mr W last updated on 13/Mar/20

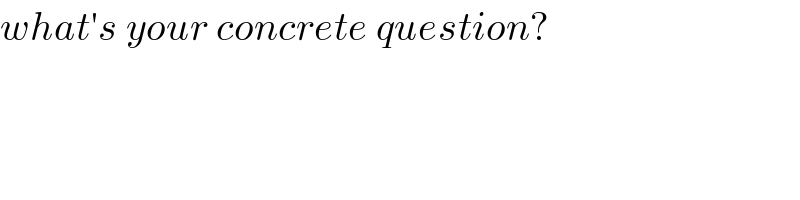
what′s your concrete question?

$${what}'{s}\:{your}\:{concrete}\:{question}? \\ $$

Commented by Power last updated on 13/Mar/20

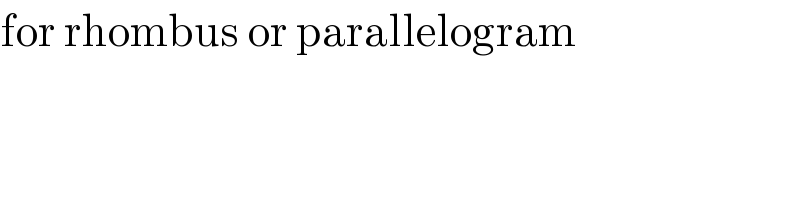
for rhombus or parallelogram

$$\mathrm{for}\:\mathrm{rhombus}\:\mathrm{or}\:\mathrm{parallelogram} \\ $$

Commented by Power last updated on 13/Mar/20

is it true that in a parallelogram, then angle will be changed.

$$\mathrm{is}\:\mathrm{it}\:\mathrm{true}\:\mathrm{that}\:\mathrm{in}\:\:\mathrm{a}\:\:\mathrm{parallelogram},\:\mathrm{then}\:\mathrm{angle}\:\mathrm{will}\:\mathrm{be}\:\mathrm{changed}. \\ $$

Commented by Power last updated on 13/Mar/20

thanks

$$\mathrm{thanks} \\ $$

Commented by Power last updated on 13/Mar/20

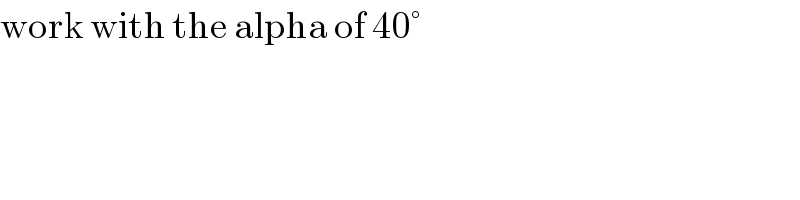
work with the alpha of 40°

$$\mathrm{work}\:\mathrm{with}\:\mathrm{the}\:\mathrm{alpha}\:\mathrm{of}\:\mathrm{40}° \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com