
Question Number 84420 by Power last updated on 12/Mar/20
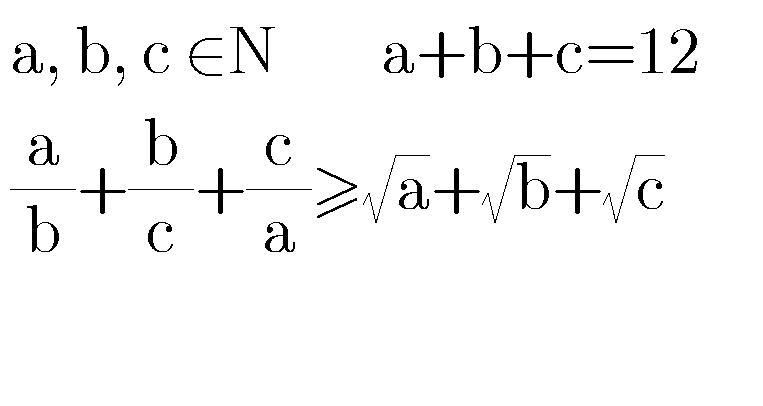
Commented by Power last updated on 12/Mar/20

$$\mathrm{prove}\:\mathrm{it} \\ $$
Commented by Power last updated on 12/Mar/20
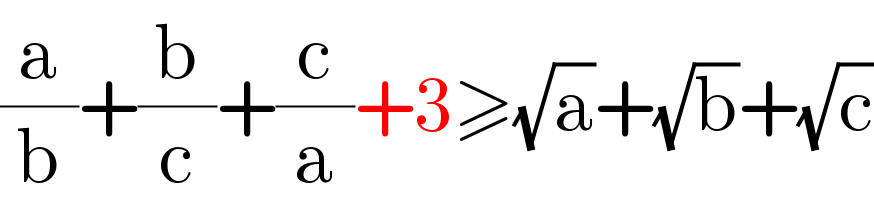
$$\frac{\mathrm{a}}{\mathrm{b}}+\frac{\mathrm{b}}{\mathrm{c}}+\frac{\mathrm{c}}{\mathrm{a}}+\mathrm{3}\geqslant\sqrt{\mathrm{a}}+\sqrt{\mathrm{b}}+\sqrt{\mathrm{c}} \\ $$
Answered by mind is power last updated on 12/Mar/20
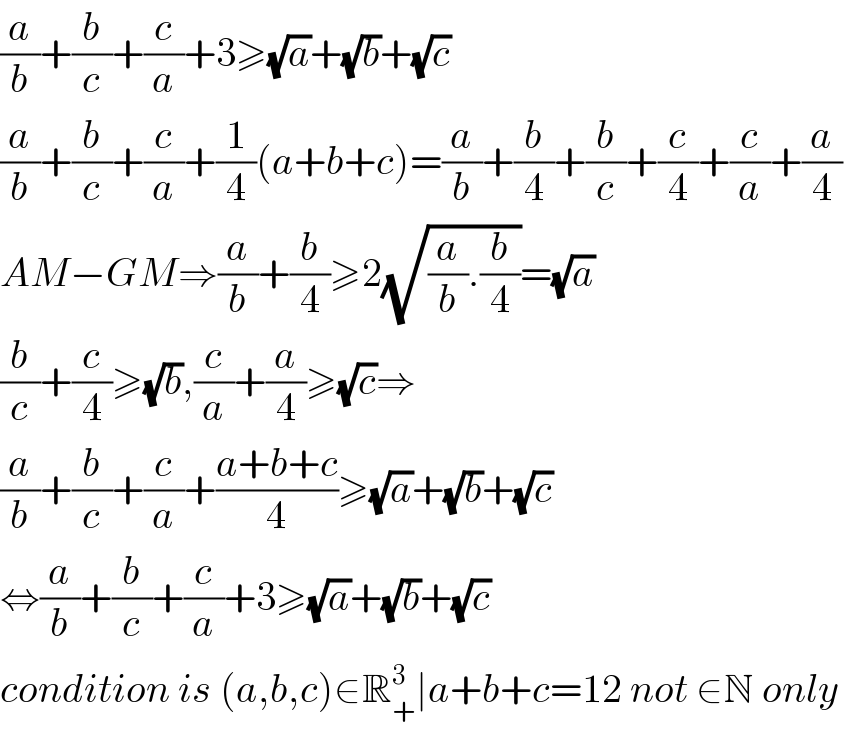
$$\frac{{a}}{{b}}+\frac{{b}}{{c}}+\frac{{c}}{{a}}+\mathrm{3}\geqslant\sqrt{{a}}+\sqrt{{b}}+\sqrt{{c}} \\ $$$$\frac{{a}}{{b}}+\frac{{b}}{{c}}+\frac{{c}}{{a}}+\frac{\mathrm{1}}{\mathrm{4}}\left({a}+{b}+{c}\right)=\frac{{a}}{{b}}+\frac{{b}}{\mathrm{4}}+\frac{{b}}{{c}}+\frac{{c}}{\mathrm{4}}+\frac{{c}}{{a}}+\frac{{a}}{\mathrm{4}}\: \\ $$$${AM}−{GM}\Rightarrow\frac{{a}}{{b}}+\frac{{b}}{\mathrm{4}}\geqslant\mathrm{2}\sqrt{\frac{{a}}{{b}}.\frac{{b}}{\mathrm{4}}}=\sqrt{{a}} \\ $$$$\frac{{b}}{{c}}+\frac{{c}}{\mathrm{4}}\geqslant\sqrt{{b}},\frac{{c}}{{a}}+\frac{{a}}{\mathrm{4}}\geqslant\sqrt{{c}}\Rightarrow \\ $$$$\frac{{a}}{{b}}+\frac{{b}}{{c}}+\frac{{c}}{{a}}+\frac{{a}+{b}+{c}}{\mathrm{4}}\geqslant\sqrt{{a}}+\sqrt{{b}}+\sqrt{{c}} \\ $$$$\Leftrightarrow\frac{{a}}{{b}}+\frac{{b}}{{c}}+\frac{{c}}{{a}}+\mathrm{3}\geqslant\sqrt{{a}}+\sqrt{{b}}+\sqrt{{c}} \\ $$$${condition}\:{is}\:\left({a},{b},{c}\right)\in\mathbb{R}_{+} ^{\mathrm{3}} \mid{a}+{b}+{c}=\mathrm{12}\:{not}\:\in\mathbb{N}\:{only} \\ $$
Commented by Power last updated on 13/Mar/20

$$\mathrm{thanks} \\ $$
Commented by mind is power last updated on 13/Mar/20

$${pleasur} \\ $$
