Question and Answers Forum

All Questions      Topic List

Matrices and Determinants Questions

Previous in All Question      Next in All Question      

Previous in Matrices and Determinants      Next in Matrices and Determinants      

Question Number 84068 by Power last updated on 09/Mar/20

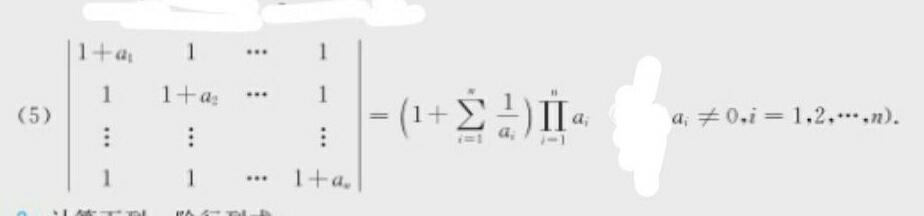
Commented by Power last updated on 09/Mar/20

prove it please

$$\boldsymbol{\mathrm{prove}}\:\boldsymbol{\mathrm{it}}\:\boldsymbol{\mathrm{please}} \\ $$

Commented by Power last updated on 09/Mar/20

please see

$$\boldsymbol{\mathrm{please}}\:\boldsymbol{\mathrm{see}} \\ $$

Commented by TANMAY PANACEA last updated on 09/Mar/20

Commented by arcana last updated on 20/Mar/20

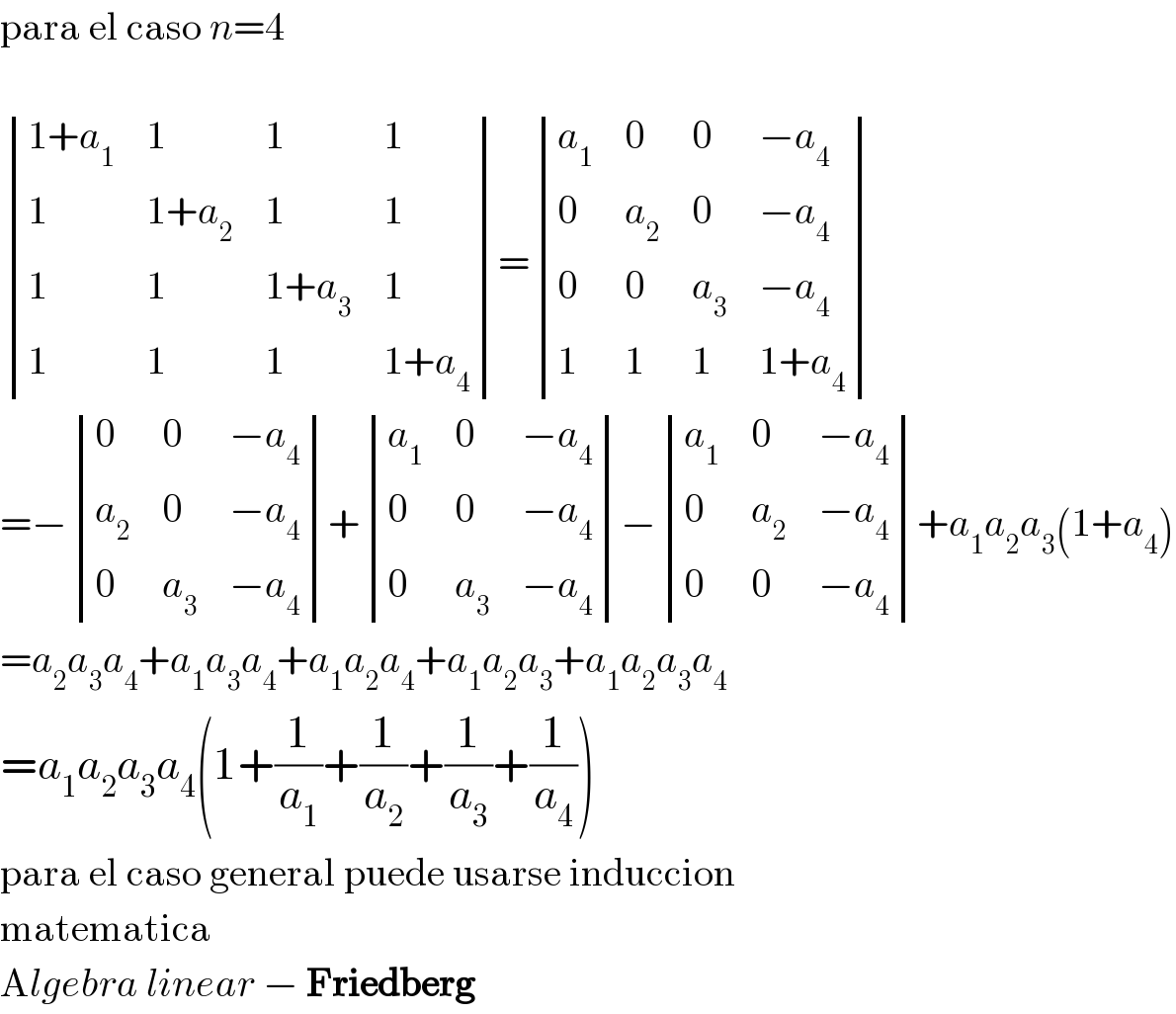
para el caso n=4 determinant (((1+a_1 ),1,1,1),(1,(1+a_2 ),1,1),(1,1,(1+a_3 ),1),(1,1,1,(1+a_4 )))= determinant ((a_1 ,0,0,(−a_4 )),(0,a_2 ,0,(−a_4 )),(0,0,a_3 ,(−a_4 )),(1,1,1,(1+a_4 ))) =− determinant ((0,0,(−a_4 )),(a_2 ,0,(−a_4 )),(0,a_3 ,(−a_4 )))+ determinant ((a_1 ,0,(−a_4 )),(0,0,(−a_4 )),(0,a_3 ,(−a_4 )))− determinant ((a_1 ,0,(−a_4 )),(0,a_2 ,(−a_4 )),(0,0,(−a_4 )))+a_1 a_2 a_3 (1+a_4 ) =a_2 a_3 a_4 +a_1 a_3 a_4 +a_1 a_2 a_4 +a_1 a_2 a_3 +a_1 a_2 a_3 a_4 =a_1 a_2 a_3 a_4 (1+(1/a_1 )+(1/a_2 )+(1/a_3 )+(1/a_4 )) para el caso general puede usarse induccion matematica Algebra linear − Friedberg

$$\mathrm{para}\:\mathrm{el}\:\mathrm{caso}\:{n}=\mathrm{4} \\ $$$$ \\ $$$$\begin{vmatrix}{\mathrm{1}+{a}_{\mathrm{1}} }&{\mathrm{1}}&{\mathrm{1}}&{\mathrm{1}}\\{\mathrm{1}}&{\mathrm{1}+{a}_{\mathrm{2}} }&{\mathrm{1}}&{\mathrm{1}}\\{\mathrm{1}}&{\mathrm{1}}&{\mathrm{1}+{a}_{\mathrm{3}} }&{\mathrm{1}}\\{\mathrm{1}}&{\mathrm{1}}&{\mathrm{1}}&{\mathrm{1}+{a}_{\mathrm{4}} }\end{vmatrix}=\begin{vmatrix}{{a}_{\mathrm{1}} }&{\mathrm{0}}&{\mathrm{0}}&{−{a}_{\mathrm{4}} }\\{\mathrm{0}}&{{a}_{\mathrm{2}} }&{\mathrm{0}}&{−{a}_{\mathrm{4}} }\\{\mathrm{0}}&{\mathrm{0}}&{{a}_{\mathrm{3}} }&{−{a}_{\mathrm{4}} }\\{\mathrm{1}}&{\mathrm{1}}&{\mathrm{1}}&{\mathrm{1}+{a}_{\mathrm{4}} }\end{vmatrix} \\ $$$$=−\begin{vmatrix}{\mathrm{0}}&{\mathrm{0}}&{−{a}_{\mathrm{4}} }\\{{a}_{\mathrm{2}} }&{\mathrm{0}}&{−{a}_{\mathrm{4}} }\\{\mathrm{0}}&{{a}_{\mathrm{3}} }&{−{a}_{\mathrm{4}} }\end{vmatrix}+\begin{vmatrix}{{a}_{\mathrm{1}} }&{\mathrm{0}}&{−{a}_{\mathrm{4}} }\\{\mathrm{0}}&{\mathrm{0}}&{−{a}_{\mathrm{4}} }\\{\mathrm{0}}&{{a}_{\mathrm{3}} }&{−{a}_{\mathrm{4}} }\end{vmatrix}−\begin{vmatrix}{{a}_{\mathrm{1}} }&{\mathrm{0}}&{−{a}_{\mathrm{4}} }\\{\mathrm{0}}&{{a}_{\mathrm{2}} }&{−{a}_{\mathrm{4}} }\\{\mathrm{0}}&{\mathrm{0}}&{−{a}_{\mathrm{4}} }\end{vmatrix}+{a}_{\mathrm{1}} {a}_{\mathrm{2}} {a}_{\mathrm{3}} \left(\mathrm{1}+{a}_{\mathrm{4}} \right) \\ $$$$={a}_{\mathrm{2}} {a}_{\mathrm{3}} {a}_{\mathrm{4}} +{a}_{\mathrm{1}} {a}_{\mathrm{3}} {a}_{\mathrm{4}} +{a}_{\mathrm{1}} {a}_{\mathrm{2}} {a}_{\mathrm{4}} +{a}_{\mathrm{1}} {a}_{\mathrm{2}} {a}_{\mathrm{3}} +{a}_{\mathrm{1}} {a}_{\mathrm{2}} {a}_{\mathrm{3}} {a}_{\mathrm{4}} \\ $$$$={a}_{\mathrm{1}} {a}_{\mathrm{2}} {a}_{\mathrm{3}} {a}_{\mathrm{4}} \left(\mathrm{1}+\frac{\mathrm{1}}{{a}_{\mathrm{1}} }+\frac{\mathrm{1}}{{a}_{\mathrm{2}} }+\frac{\mathrm{1}}{{a}_{\mathrm{3}} }+\frac{\mathrm{1}}{{a}_{\mathrm{4}} }\right) \\ $$$$\mathrm{para}\:\mathrm{el}\:\mathrm{caso}\:\mathrm{general}\:\mathrm{puede}\:\mathrm{usarse}\:\mathrm{induccion} \\ $$$$\mathrm{matematica} \\ $$$$\mathrm{A}{lgebra}\:{linear}\:−\:\boldsymbol{\mathrm{Friedberg}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com