Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 82431 by Power last updated on 21/Feb/20

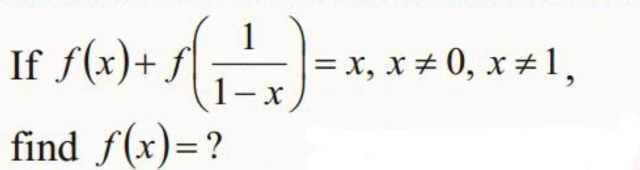
Commented by Power last updated on 21/Feb/20

solution sir please prove it

$$\mathrm{solution}\:\mathrm{sir}\:\mathrm{please}\:\mathrm{prove}\:\:\mathrm{it} \\ $$

Commented by mr W last updated on 21/Feb/20

what′s your result sir? f(x)=?

$${what}'{s}\:{your}\:{result}\:{sir}?\:{f}\left({x}\right)=? \\ $$

Commented by mr W last updated on 21/Feb/20

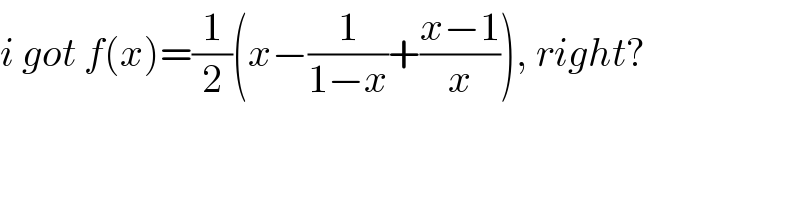
i got f(x)=(1/2)(x−(1/(1−x))+((x−1)/x)), right?

$${i}\:{got}\:{f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left({x}−\frac{\mathrm{1}}{\mathrm{1}−{x}}+\frac{{x}−\mathrm{1}}{{x}}\right),\:{right}? \\ $$

Commented by Power last updated on 21/Feb/20

f(x)=((x^3 −x+1)/(2x(x−1)))

$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{x}^{\mathrm{3}} −\mathrm{x}+\mathrm{1}}{\mathrm{2x}\left(\mathrm{x}−\mathrm{1}\right)} \\ $$

Commented by mr W last updated on 21/Feb/20

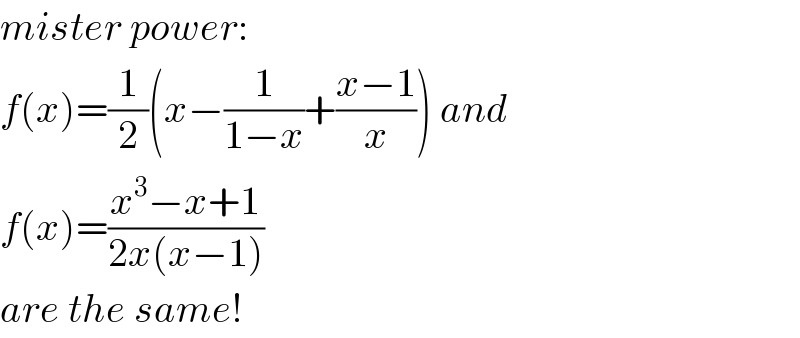
mister power: f(x)=(1/2)(x−(1/(1−x))+((x−1)/x)) and f(x)=((x^3 −x+1)/(2x(x−1))) are the same!

$${mister}\:{power}: \\ $$$${f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left({x}−\frac{\mathrm{1}}{\mathrm{1}−{x}}+\frac{{x}−\mathrm{1}}{{x}}\right)\:{and}\: \\ $$$${f}\left({x}\right)=\frac{{x}^{\mathrm{3}} −{x}+\mathrm{1}}{\mathrm{2}{x}\left({x}−\mathrm{1}\right)} \\ $$$${are}\:{the}\:{same}! \\ $$

Answered by mr W last updated on 21/Feb/20

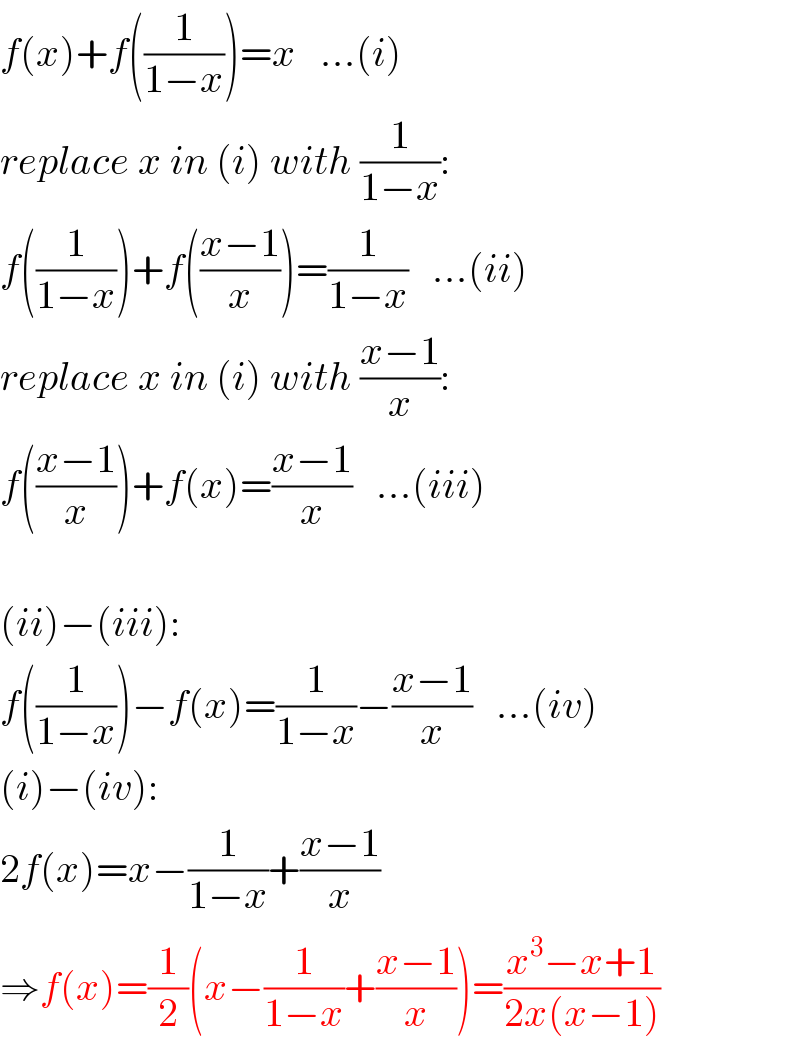
f(x)+f((1/(1−x)))=x ...(i) replace x in (i) with (1/(1−x)): f((1/(1−x)))+f(((x−1)/x))=(1/(1−x)) ...(ii) replace x in (i) with ((x−1)/x): f(((x−1)/x))+f(x)=((x−1)/x) ...(iii) (ii)−(iii): f((1/(1−x)))−f(x)=(1/(1−x))−((x−1)/x) ...(iv) (i)−(iv): 2f(x)=x−(1/(1−x))+((x−1)/x) ⇒f(x)=(1/2)(x−(1/(1−x))+((x−1)/x))=((x^3 −x+1)/(2x(x−1)))

$${f}\left({x}\right)+{f}\left(\frac{\mathrm{1}}{\mathrm{1}−{x}}\right)={x}\:\:\:...\left({i}\right) \\ $$$${replace}\:{x}\:{in}\:\left({i}\right)\:{with}\:\frac{\mathrm{1}}{\mathrm{1}−{x}}: \\ $$$${f}\left(\frac{\mathrm{1}}{\mathrm{1}−{x}}\right)+{f}\left(\frac{{x}−\mathrm{1}}{{x}}\right)=\frac{\mathrm{1}}{\mathrm{1}−{x}}\:\:\:...\left({ii}\right) \\ $$$${replace}\:{x}\:{in}\:\left({i}\right)\:{with}\:\frac{{x}−\mathrm{1}}{{x}}: \\ $$$${f}\left(\frac{{x}−\mathrm{1}}{{x}}\right)+{f}\left({x}\right)=\frac{{x}−\mathrm{1}}{{x}}\:\:\:...\left({iii}\right) \\ $$$$ \\ $$$$\left({ii}\right)−\left({iii}\right): \\ $$$${f}\left(\frac{\mathrm{1}}{\mathrm{1}−{x}}\right)−{f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{1}−{x}}−\frac{{x}−\mathrm{1}}{{x}}\:\:\:...\left({iv}\right) \\ $$$$\left({i}\right)−\left({iv}\right): \\ $$$$\mathrm{2}{f}\left({x}\right)={x}−\frac{\mathrm{1}}{\mathrm{1}−{x}}+\frac{{x}−\mathrm{1}}{{x}} \\ $$$$\Rightarrow{f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left({x}−\frac{\mathrm{1}}{\mathrm{1}−{x}}+\frac{{x}−\mathrm{1}}{{x}}\right)=\frac{{x}^{\mathrm{3}} −{x}+\mathrm{1}}{\mathrm{2}{x}\left({x}−\mathrm{1}\right)} \\ $$

Commented by Power last updated on 21/Feb/20

yes thank you sir

$$\mathrm{yes}\:\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com