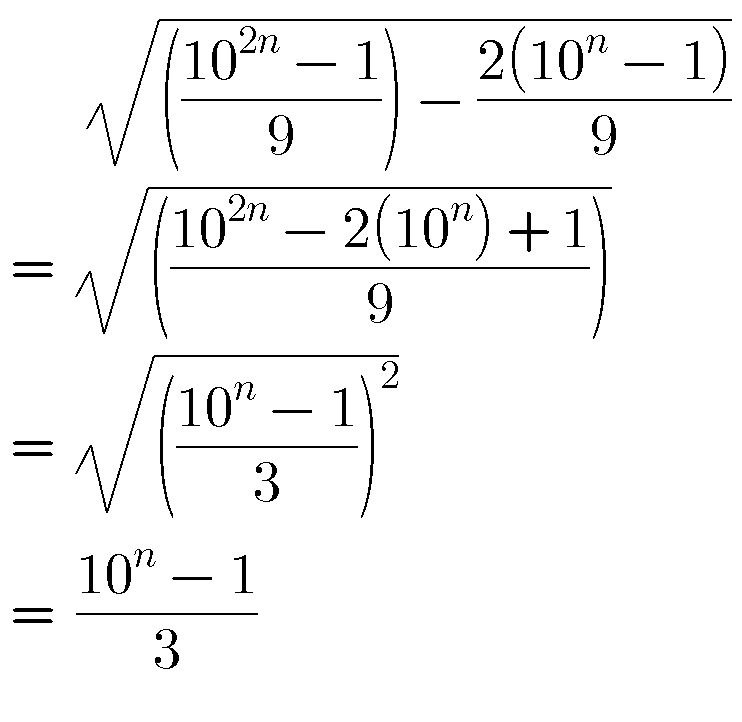Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 80068 by Pratah last updated on 30/Jan/20

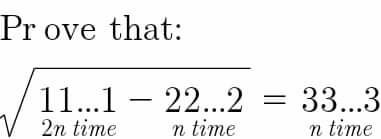
Commented by mr W last updated on 30/Jan/20

sir Pratah: are you student? teacher? professor? what′s the source of your questions?

$${sir}\:{Pratah}: \\ $$$${are}\:{you}\:{student}?\:{teacher}?\:{professor}? \\ $$$${what}'{s}\:{the}\:{source}\:{of}\:{your}\:{questions}? \\ $$

Commented by Pratah last updated on 30/Jan/20

student.plz solution

$$\mathrm{student}.\mathrm{plz}\:\mathrm{solution} \\ $$

Commented by Pratah last updated on 30/Jan/20

sir? john santu

$$\mathrm{sir}?\:\:\:\mathrm{john}\:\mathrm{santu} \\ $$

Answered by mr W last updated on 30/Jan/20

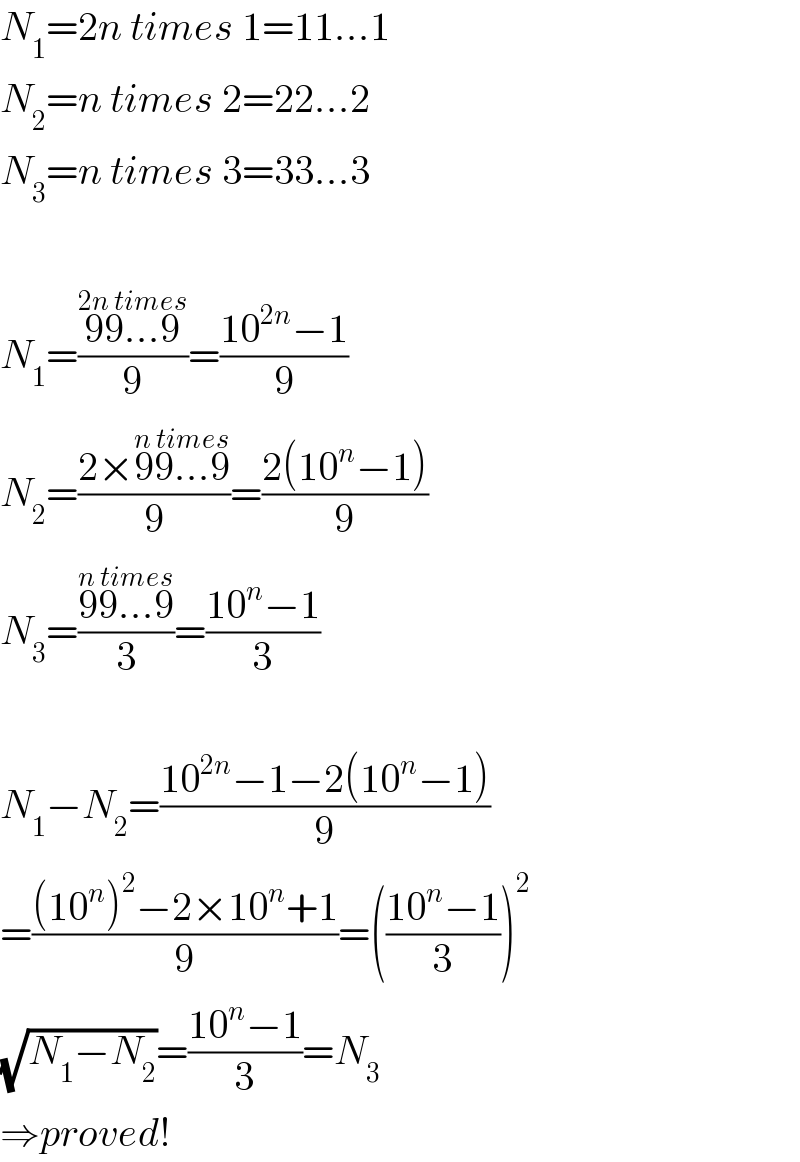
N_1 =2n times 1=11...1 N_2 =n times 2=22...2 N_3 =n times 3=33...3 N_1 =((99...9^(2n times) )/9)=((10^(2n) −1)/9) N_2 =((2×99...9^(n times) )/9)=((2(10^n −1))/9) N_3 =((99...9^(n times) )/3)=((10^n −1)/3) N_1 −N_2 =((10^(2n) −1−2(10^n −1))/9) =(((10^n )^2 −2×10^n +1)/9)=(((10^n −1)/3))^2 (√(N_1 −N_2 ))=((10^n −1)/3)=N_3 ⇒proved!

$${N}_{\mathrm{1}} =\mathrm{2}{n}\:{times}\:\mathrm{1}=\mathrm{11}...\mathrm{1} \\ $$$${N}_{\mathrm{2}} ={n}\:{times}\:\mathrm{2}=\mathrm{22}...\mathrm{2} \\ $$$${N}_{\mathrm{3}} ={n}\:{times}\:\mathrm{3}=\mathrm{33}...\mathrm{3} \\ $$$$ \\ $$$${N}_{\mathrm{1}} =\frac{\overset{\mathrm{2}{n}\:{times}} {\mathrm{99}...\mathrm{9}}}{\mathrm{9}}=\frac{\mathrm{10}^{\mathrm{2}{n}} −\mathrm{1}}{\mathrm{9}} \\ $$$${N}_{\mathrm{2}} =\frac{\mathrm{2}×\overset{{n}\:{times}} {\mathrm{99}...\mathrm{9}}}{\mathrm{9}}=\frac{\mathrm{2}\left(\mathrm{10}^{{n}} −\mathrm{1}\right)}{\mathrm{9}} \\ $$$${N}_{\mathrm{3}} =\frac{\overset{{n}\:{times}} {\mathrm{99}...\mathrm{9}}}{\mathrm{3}}=\frac{\mathrm{10}^{{n}} −\mathrm{1}}{\mathrm{3}} \\ $$$$ \\ $$$${N}_{\mathrm{1}} −{N}_{\mathrm{2}} =\frac{\mathrm{10}^{\mathrm{2}{n}} −\mathrm{1}−\mathrm{2}\left(\mathrm{10}^{{n}} −\mathrm{1}\right)}{\mathrm{9}} \\ $$$$=\frac{\left(\mathrm{10}^{{n}} \right)^{\mathrm{2}} −\mathrm{2}×\mathrm{10}^{{n}} +\mathrm{1}}{\mathrm{9}}=\left(\frac{\mathrm{10}^{{n}} −\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} \\ $$$$\sqrt{{N}_{\mathrm{1}} −{N}_{\mathrm{2}} }=\frac{\mathrm{10}^{{n}} −\mathrm{1}}{\mathrm{3}}={N}_{\mathrm{3}} \\ $$$$\Rightarrow{proved}! \\ $$

Commented by Pratah last updated on 30/Jan/20

thanks

$$\mathrm{thanks} \\ $$

Answered by naka3546 last updated on 31/Jan/20

Terms of Service

Privacy Policy

Contact: info@tinkutara.com