
Question Number 7803 by Tawakalitu. last updated on 16/Sep/16
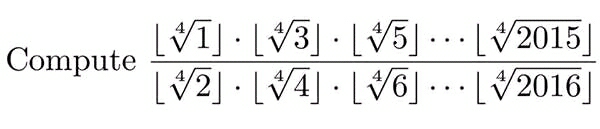
Answered by Rasheed Soomro last updated on 16/Sep/16

$$\left(\frac{\mathrm{1}×\mathrm{3}×\mathrm{5}×...×\mathrm{2015}}{\mathrm{2}×\mathrm{4}×\mathrm{6}×...×\mathrm{2016}}\right)^{\mathrm{1}/\mathrm{4}} \\ $$$$\left(\frac{\mathrm{2015}!/\left(\mathrm{2}.\mathrm{4}.\mathrm{6}.....\mathrm{2014}\right.}{\mathrm{2}.\mathrm{4}.\mathrm{6}.....\mathrm{2016}}\right)^{\mathrm{1}/\mathrm{4}} \\ $$$$\left(\frac{\mathrm{2015}!}{\left(\mathrm{2}.\mathrm{4}.\mathrm{6}....\mathrm{2014}\right)\left(\mathrm{2}.\mathrm{4}.\mathrm{6}.....\mathrm{2016}\right)}\right)^{\mathrm{1}/\mathrm{4}} \\ $$$$\left(\frac{\mathrm{2015}!}{\left(\mathrm{2}.\mathrm{4}.\mathrm{6}....\mathrm{2014}\right)^{\mathrm{2}} \left(\mathrm{2015}.\mathrm{2016}\right)}\right)^{\mathrm{1}/\mathrm{4}} \\ $$$$\left(\frac{\mathrm{2015}!}{\mathrm{2}^{\mathrm{2014}} \left(\mathrm{1}.\mathrm{2}.\mathrm{3}....\mathrm{1007}\right)^{\mathrm{2}} \left(\mathrm{2015}.\mathrm{1008}.\mathrm{2}\right)}\right)^{\mathrm{1}/\mathrm{4}} \\ $$$$\left(\frac{\mathrm{2015}!}{\mathrm{2}^{\mathrm{2015}} \left(\mathrm{1007}!\right)^{\mathrm{2}} \left(\mathrm{2015}.\mathrm{1008}\right)}\right)^{\mathrm{1}/\mathrm{4}} \\ $$$$\left(\frac{\mathrm{2014}!}{\mathrm{2}^{\mathrm{2015}} \left(\mathrm{1008}!\right)\left(\mathrm{1007}!\right)}\right)^{\mathrm{1}/\mathrm{4}} \\ $$$$ \\ $$
Commented by Tawakalitu. last updated on 16/Sep/16
$${Thanks}\:{so}\:{much}\:{sir}.\:{is}\:{that}\:{all}\:? \\ $$
Commented by Tawakalitu. last updated on 16/Sep/16
$${Thanks}\:{so}\:{much}\:{sir}.\:{is}\:{that}\:{all}\:? \\ $$
