
Question Number 77390 by Maclaurin Stickker last updated on 05/Jan/20
Commented by Maclaurin Stickker last updated on 05/Jan/20

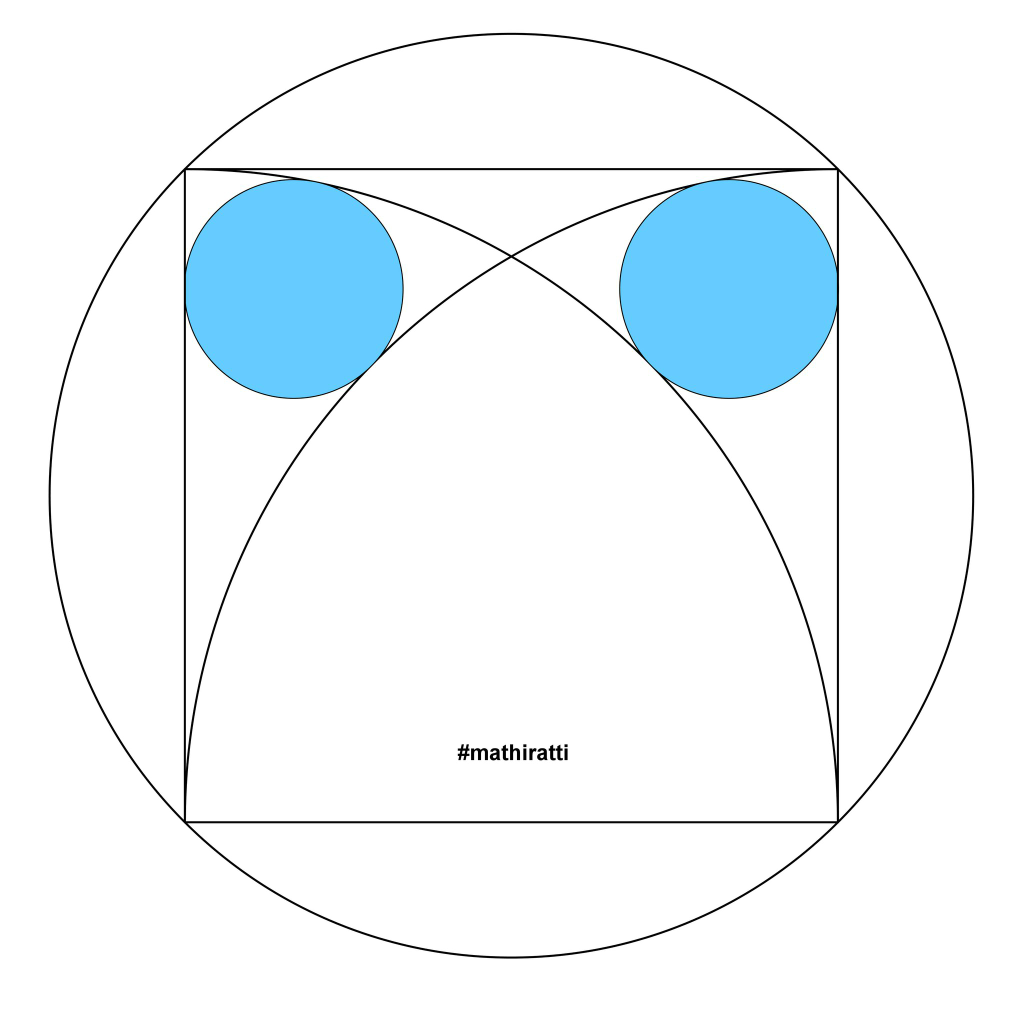
$${find}\:{the}\:{radius}\:{of}\:{the}\:{shaded}\: \\ $$$${circumference}\:{as}\:{a}\:{function}\:{of} \\ $$$${side}\:{a}\:{of}\:{the}\:{square}. \\ $$
Answered by jagoll last updated on 06/Jan/20

$$\mathrm{r}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\:=\:\mathrm{a}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right) \\ $$$$\mathrm{r}\:=\:\mathrm{a}\left(\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}\right) \\ $$
Commented by mr W last updated on 06/Jan/20
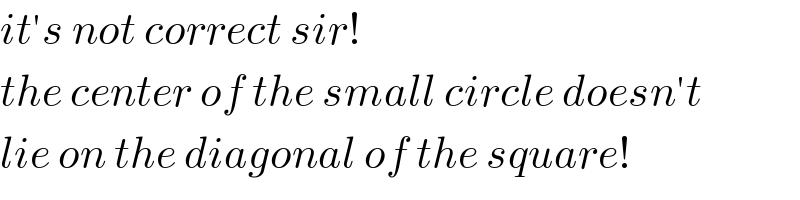
$${it}'{s}\:{not}\:{correct}\:{sir}! \\ $$$${the}\:{center}\:{of}\:{the}\:{small}\:{circle}\:{doesn}'{t} \\ $$$${lie}\:{on}\:{the}\:{diagonal}\:{of}\:{the}\:{square}! \\ $$
Commented by jagoll last updated on 06/Jan/20

$$\:\:{o}\:{yes}\:{sir}\:{i}\:{agree} \\ $$
Answered by mr W last updated on 06/Jan/20
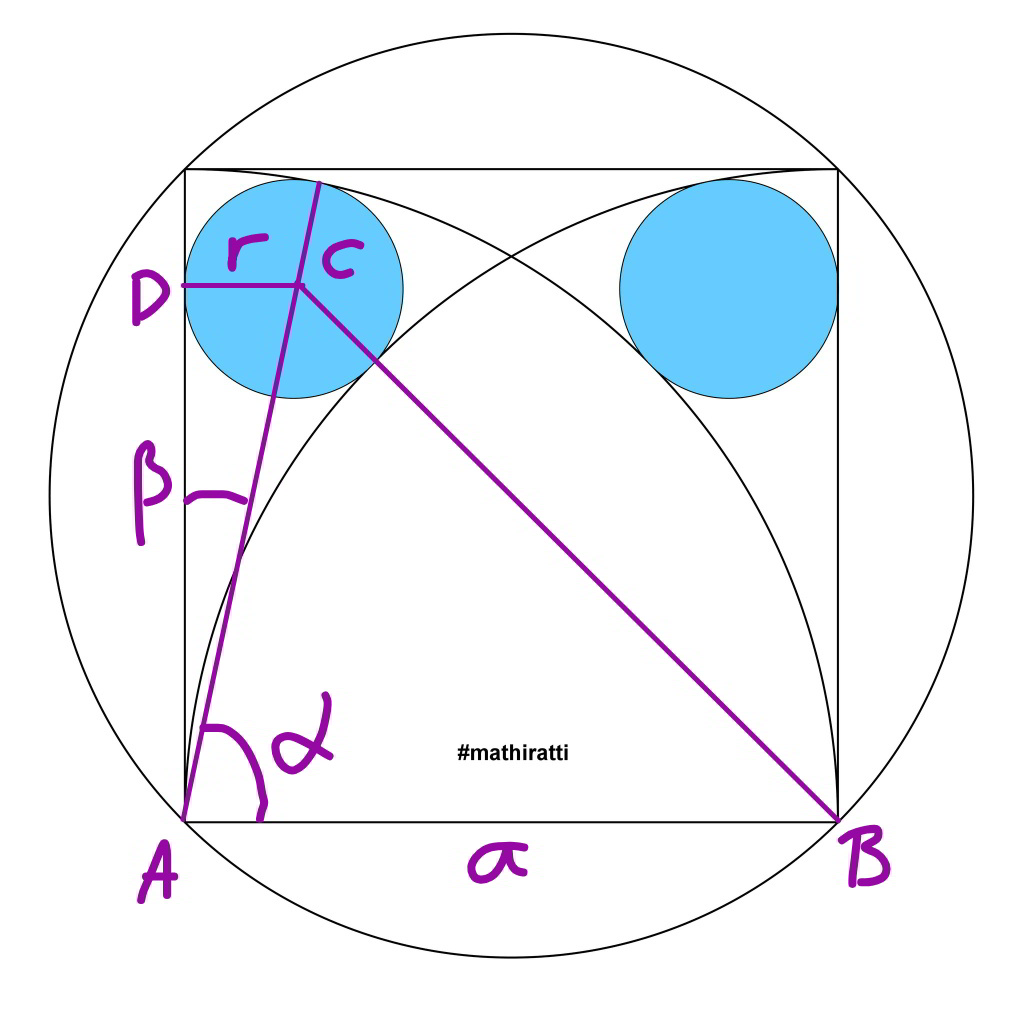
Commented by mr W last updated on 06/Jan/20
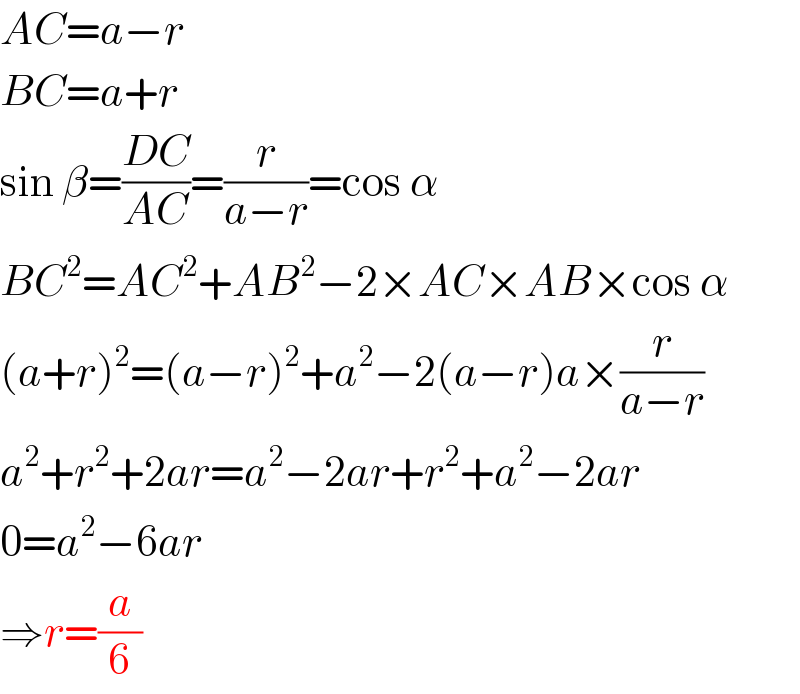
$${AC}={a}−{r} \\ $$$${BC}={a}+{r} \\ $$$$\mathrm{sin}\:\beta=\frac{{DC}}{{AC}}=\frac{{r}}{{a}−{r}}=\mathrm{cos}\:\alpha \\ $$$${BC}^{\mathrm{2}} ={AC}^{\mathrm{2}} +{AB}^{\mathrm{2}} −\mathrm{2}×{AC}×{AB}×\mathrm{cos}\:\alpha \\ $$$$\left({a}+{r}\right)^{\mathrm{2}} =\left({a}−{r}\right)^{\mathrm{2}} +{a}^{\mathrm{2}} −\mathrm{2}\left({a}−{r}\right){a}×\frac{{r}}{{a}−{r}} \\ $$$${a}^{\mathrm{2}} +{r}^{\mathrm{2}} +\mathrm{2}{ar}={a}^{\mathrm{2}} −\mathrm{2}{ar}+{r}^{\mathrm{2}} +{a}^{\mathrm{2}} −\mathrm{2}{ar} \\ $$$$\mathrm{0}={a}^{\mathrm{2}} −\mathrm{6}{ar} \\ $$$$\Rightarrow{r}=\frac{{a}}{\mathrm{6}} \\ $$
Commented by mr W last updated on 06/Jan/20
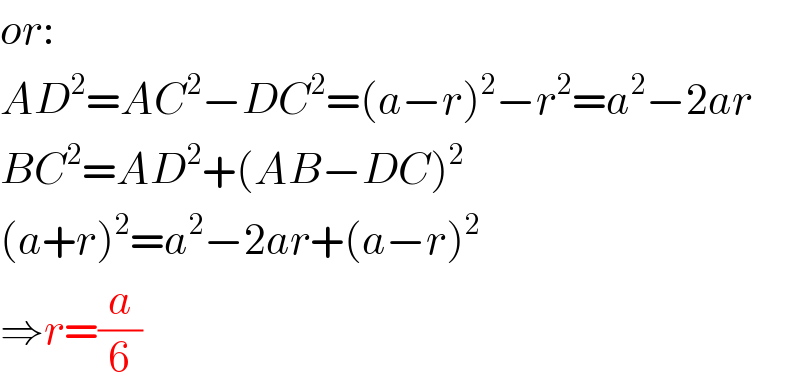
$${or}: \\ $$$${AD}^{\mathrm{2}} ={AC}^{\mathrm{2}} −{DC}^{\mathrm{2}} =\left({a}−{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} ={a}^{\mathrm{2}} −\mathrm{2}{ar} \\ $$$${BC}^{\mathrm{2}} ={AD}^{\mathrm{2}} +\left({AB}−{DC}\right)^{\mathrm{2}} \\ $$$$\left({a}+{r}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} −\mathrm{2}{ar}+\left({a}−{r}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{r}=\frac{{a}}{\mathrm{6}} \\ $$
Commented by jagoll last updated on 06/Jan/20
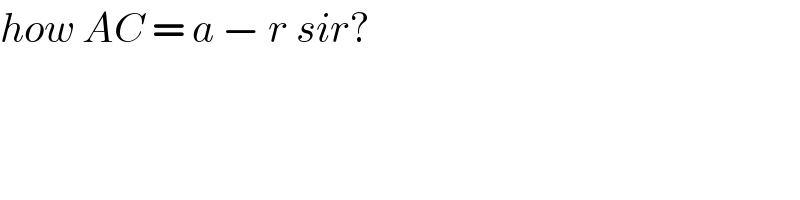
$${how}\:{AC}\:=\:{a}\:−\:{r}\:{sir}? \\ $$
Commented by mr W last updated on 06/Jan/20
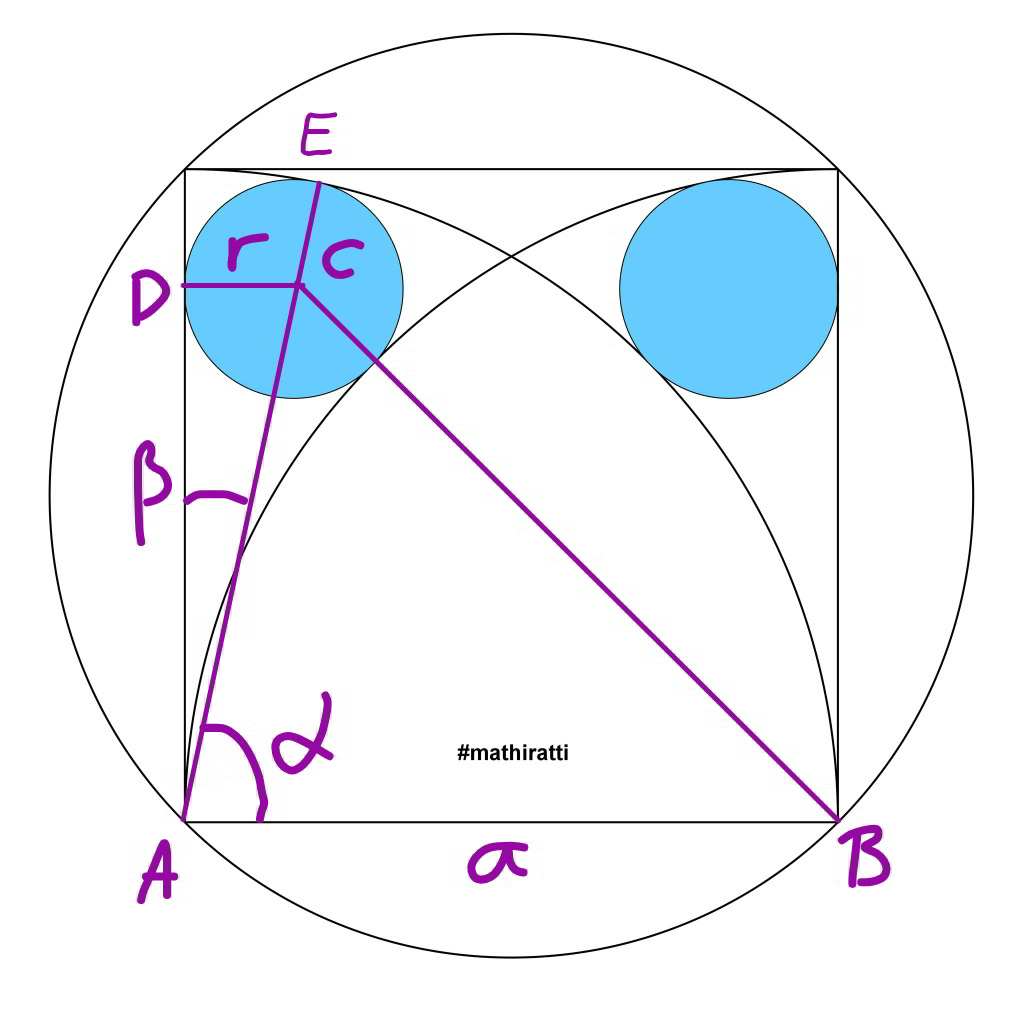
Commented by mr W last updated on 06/Jan/20
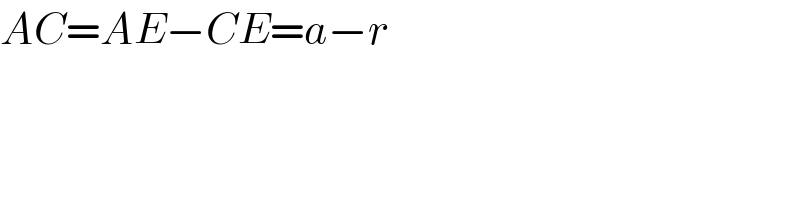
$${AC}={AE}−{CE}={a}−{r} \\ $$
Commented by Maclaurin Stickker last updated on 06/Jan/20

$${Yes},\:{Mr}\:{W},\:{you}\:{are}\:{right}! \\ $$
Commented by mr W last updated on 06/Jan/20
$${thanks}\:{for}\:{comfirming}\:{sir}! \\ $$
Commented by Tawa11 last updated on 29/Dec/21

$$\mathrm{Great}\:\mathrm{sir} \\ $$
