Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 77340 by BK last updated on 05/Jan/20

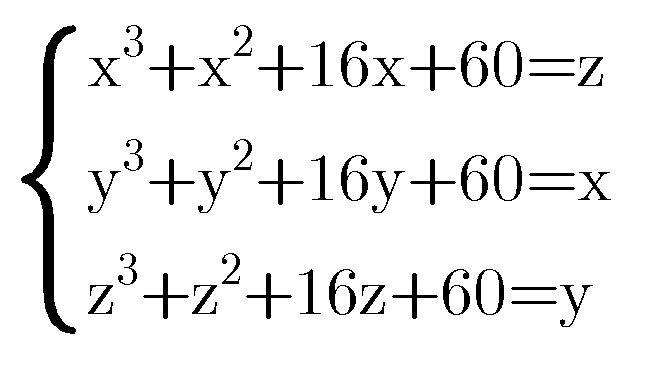
Answered by mind is power last updated on 05/Jan/20

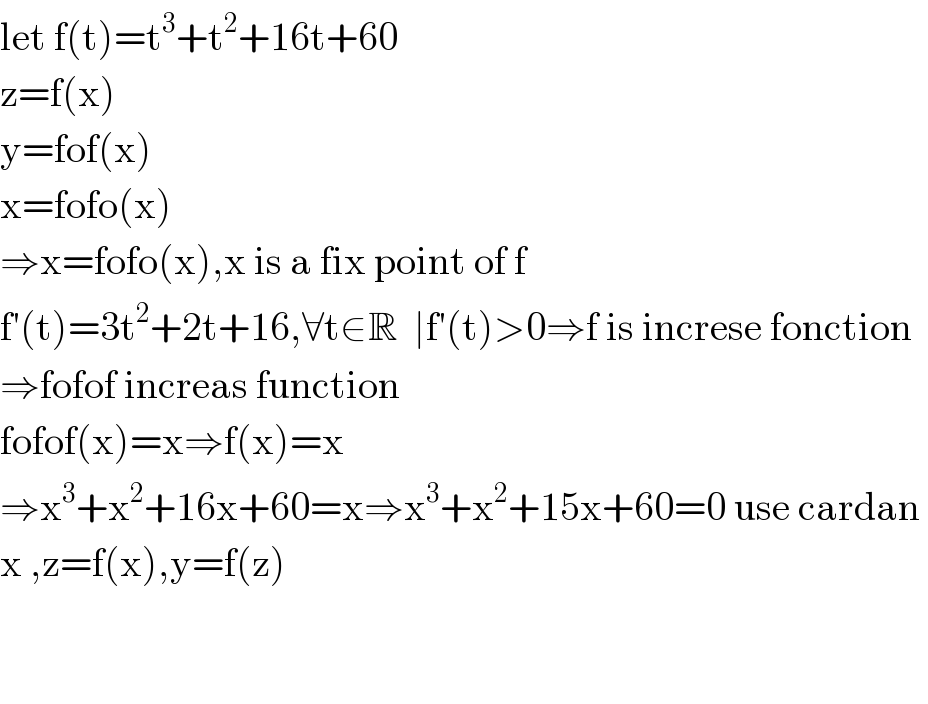
let f(t)=t^3 +t^2 +16t+60 z=f(x) y=fof(x) x=fofo(x) ⇒x=fofo(x),x is a fix point of f f′(t)=3t^2 +2t+16,∀t∈R ∣f′(t)>0⇒f is increse fonction ⇒fofof increas function fofof(x)=x⇒f(x)=x ⇒x^3 +x^2 +16x+60=x⇒x^3 +x^2 +15x+60=0 use cardan x ,z=f(x),y=f(z)

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{t}\right)=\mathrm{t}^{\mathrm{3}} +\mathrm{t}^{\mathrm{2}} +\mathrm{16t}+\mathrm{60} \\ $$$$\mathrm{z}=\mathrm{f}\left(\mathrm{x}\right) \\ $$$$\mathrm{y}=\mathrm{fof}\left(\mathrm{x}\right) \\ $$$$\mathrm{x}=\mathrm{fofo}\left(\mathrm{x}\right) \\ $$$$\Rightarrow\mathrm{x}=\mathrm{fofo}\left(\mathrm{x}\right),\mathrm{x}\:\mathrm{is}\:\mathrm{a}\:\mathrm{fix}\:\mathrm{point}\:\mathrm{of}\:\mathrm{f}\: \\ $$$$\mathrm{f}'\left(\mathrm{t}\right)=\mathrm{3t}^{\mathrm{2}} +\mathrm{2t}+\mathrm{16},\forall\mathrm{t}\in\mathbb{R}\:\:\mid\mathrm{f}'\left(\mathrm{t}\right)>\mathrm{0}\Rightarrow\mathrm{f}\:\mathrm{is}\:\mathrm{increse}\:\mathrm{fonction} \\ $$$$\Rightarrow\mathrm{fofof}\:\mathrm{increas}\:\mathrm{function} \\ $$$$\mathrm{fofof}\left(\mathrm{x}\right)=\mathrm{x}\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{3}} +\mathrm{x}^{\mathrm{2}} +\mathrm{16x}+\mathrm{60}=\mathrm{x}\Rightarrow\mathrm{x}^{\mathrm{3}} +\mathrm{x}^{\mathrm{2}} +\mathrm{15x}+\mathrm{60}=\mathrm{0}\:\mathrm{use}\:\mathrm{cardan}\: \\ $$$$\mathrm{x}\:,\mathrm{z}=\mathrm{f}\left(\mathrm{x}\right),\mathrm{y}=\mathrm{f}\left(\mathrm{z}\right) \\ $$$$ \\ $$$$ \\ $$

Commented by BK last updated on 05/Jan/20

thank you sir great!

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}\:\mathrm{great}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com