
Question Number 76830 by peter frank last updated on 30/Dec/19
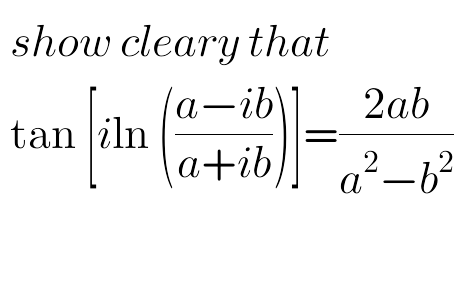
Commented by mathmax by abdo last updated on 05/Jan/20
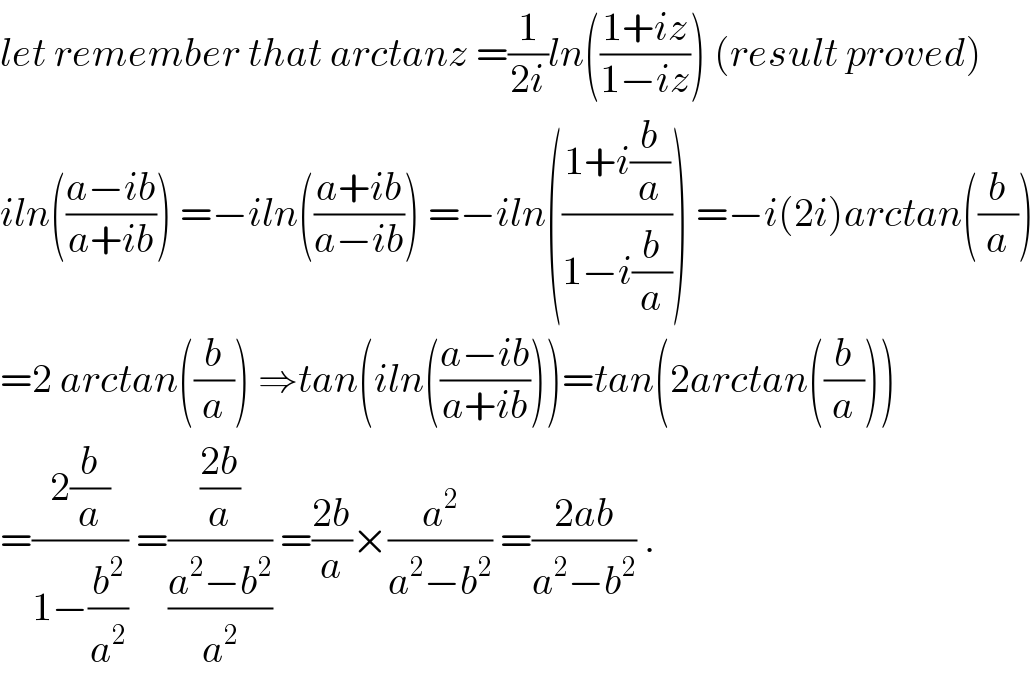
$${let}\:{remember}\:{that}\:{arctanz}\:=\frac{\mathrm{1}}{\mathrm{2}{i}}{ln}\left(\frac{\mathrm{1}+{iz}}{\mathrm{1}−{iz}}\right)\:\left({result}\:{proved}\right) \\ $$$${iln}\left(\frac{{a}−{ib}}{{a}+{ib}}\right)\:=−{iln}\left(\frac{{a}+{ib}}{{a}−{ib}}\right)\:=−{iln}\left(\frac{\mathrm{1}+{i}\frac{{b}}{{a}}}{\mathrm{1}−{i}\frac{{b}}{{a}}}\right)\:=−{i}\left(\mathrm{2}{i}\right){arctan}\left(\frac{{b}}{{a}}\right) \\ $$$$=\mathrm{2}\:{arctan}\left(\frac{{b}}{{a}}\right)\:\Rightarrow{tan}\left({iln}\left(\frac{{a}−{ib}}{{a}+{ib}}\right)\right)={tan}\left(\mathrm{2}{arctan}\left(\frac{{b}}{{a}}\right)\right) \\ $$$$=\frac{\mathrm{2}\frac{{b}}{{a}}}{\mathrm{1}−\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }}\:=\frac{\frac{\mathrm{2}{b}}{{a}}}{\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }}\:=\frac{\mathrm{2}{b}}{{a}}×\frac{{a}^{\mathrm{2}} }{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\:=\frac{\mathrm{2}{ab}}{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\:. \\ $$
Commented by peter frank last updated on 05/Jan/20

$${thank}\:{you} \\ $$
Answered by MJS last updated on 31/Dec/19
![ln (p+qi) =(1/2)ln (p^2 +q^2 ) +i arctan (q/p) i ln (p+qi) =−arctan (q/p) +i((ln (p^2 +q^2 ))/2)= [((a−bi)/(a+bi))=((a^2 −b^2 )/(a^2 +b^2 ))−((2ab)/(a^2 +b^2 ))i ⇒ p=((a^2 −b^2 )/(a^2 +b^2 )); q=−((2ab)/(a^2 +b^2 )) ⇒ p^2 +q^2 =1] =arctan ((2ab)/(a^2 −b^2 )) ⇒ tan (i ln ((a−bi)/(a+bi))) =((2ab)/(a^2 −b^2 ))](Q76839.png)
$$\mathrm{ln}\:\left({p}+{q}\mathrm{i}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)\:+\mathrm{i}\:\mathrm{arctan}\:\frac{{q}}{{p}} \\ $$$$\mathrm{i}\:\mathrm{ln}\:\left({p}+{q}\mathrm{i}\right)\:=−\mathrm{arctan}\:\frac{{q}}{{p}}\:+\mathrm{i}\frac{\mathrm{ln}\:\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)}{\mathrm{2}}= \\ $$$$\:\:\:\:\:\left[\frac{{a}−{b}\mathrm{i}}{{a}+{b}\mathrm{i}}=\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }−\frac{\mathrm{2}{ab}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\mathrm{i}\:\Rightarrow\:{p}=\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} };\:{q}=−\frac{\mathrm{2}{ab}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\:\Rightarrow\:{p}^{\mathrm{2}} +{q}^{\mathrm{2}} =\mathrm{1}\right] \\ $$$$=\mathrm{arctan}\:\frac{\mathrm{2}{ab}}{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\mathrm{tan}\:\left(\mathrm{i}\:\mathrm{ln}\:\frac{{a}−{b}\mathrm{i}}{{a}+{b}\mathrm{i}}\right)\:=\frac{\mathrm{2}{ab}}{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} } \\ $$
Commented by peter frank last updated on 31/Dec/19
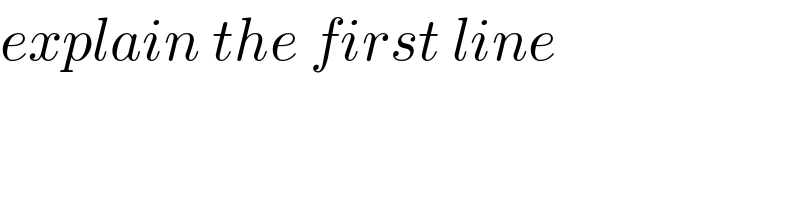
$${explain}\:{the}\:{first}\:{line}\: \\ $$
Commented by mr W last updated on 31/Dec/19
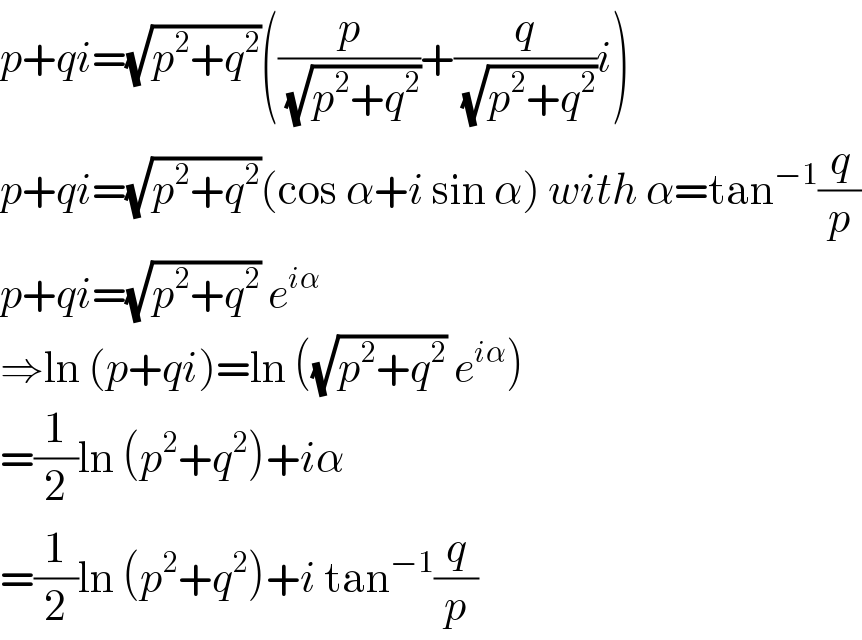
$${p}+{qi}=\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} }\left(\frac{{p}}{\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} }}+\frac{{q}}{\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} }}{i}\right) \\ $$$${p}+{qi}=\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} }\left(\mathrm{cos}\:\alpha+{i}\:\mathrm{sin}\:\alpha\right)\:{with}\:\alpha=\mathrm{tan}^{−\mathrm{1}} \frac{{q}}{{p}} \\ $$$${p}+{qi}=\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} }\:{e}^{{i}\alpha} \\ $$$$\Rightarrow\mathrm{ln}\:\left({p}+{qi}\right)=\mathrm{ln}\:\left(\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} }\:{e}^{{i}\alpha} \right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)+{i}\alpha \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)+{i}\:\mathrm{tan}^{−\mathrm{1}} \frac{{q}}{{p}} \\ $$
Commented by peter frank last updated on 31/Dec/19
$${thank}\:{you}\:{sir}\:{for}\:{ellaboration} \\ $$
