
Question Number 76317 by Master last updated on 26/Dec/19
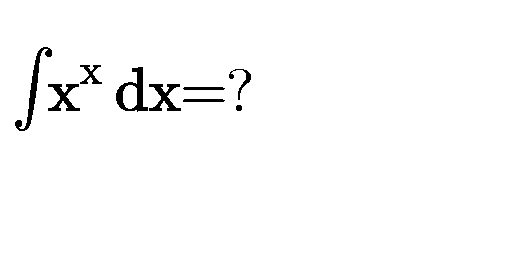
Commented by john santu last updated on 26/Dec/19
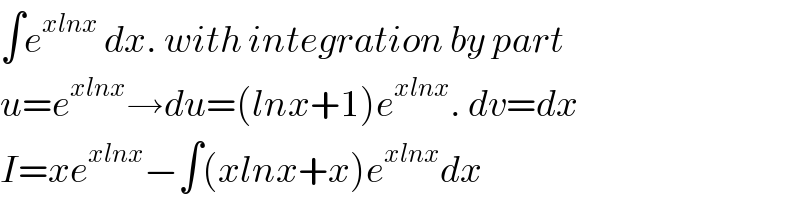
$$\int{e}^{{xlnx}} \:{dx}.\:{with}\:{integration}\:{by}\:{part} \\ $$$${u}={e}^{{xlnx}} \rightarrow{du}=\left({lnx}+\mathrm{1}\right){e}^{{xlnx}} .\:{dv}={dx}\: \\ $$$${I}={xe}^{{xlnx}} −\int\left({xlnx}+{x}\right){e}^{{xlnx}} {dx} \\ $$
Commented by turbo msup by abdo last updated on 26/Dec/19
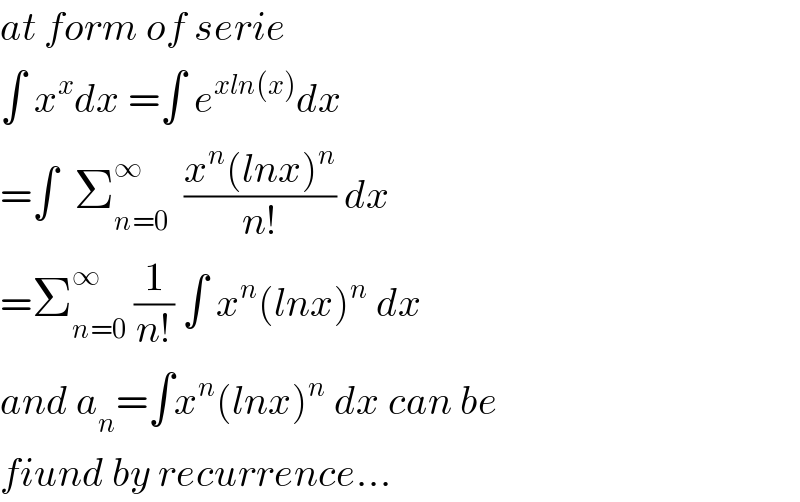
$${at}\:{form}\:{of}\:{serie} \\ $$$$\int\:{x}^{{x}} {dx}\:=\int\:{e}^{{xln}\left({x}\right)} {dx} \\ $$$$=\int\:\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{{x}^{{n}} \left({lnx}\right)^{{n}} }{{n}!}\:{dx} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{{n}!}\:\int\:{x}^{{n}} \left({lnx}\right)^{{n}} \:{dx} \\ $$$${and}\:{a}_{{n}} =\int{x}^{{n}} \left({lnx}\right)^{{n}} \:{dx}\:{can}\:{be} \\ $$$${fiund}\:{by}\:{recurrence}... \\ $$
Commented by mr W last updated on 27/Dec/19

$${i}\:{see}\:{absolutely}\:{no}\:{sense}\:{for}\: \\ $$$${repeated}\:{posting}\:{questions}\:{like} \\ $$$$\int{x}^{{x}} {dx}\:{or}\:\int{x}!{dx}. \\ $$
