
Question Number 76143 by Master last updated on 24/Dec/19
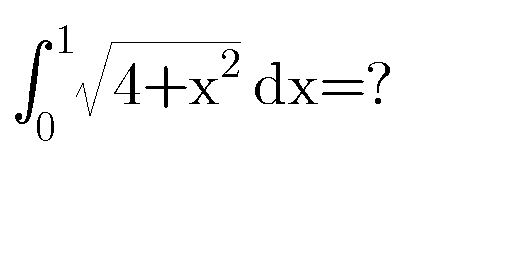
Commented by mathmax by abdo last updated on 24/Dec/19
![let I =∫_0 ^1 (√(4+x^2 ))dx changement x=2sh(t) give I =∫_0 ^(argsh((1/2))) 2ch(t)2ch(t)dt =4 ∫_0 ^(ln((1/2)+(√(1+(1/4))))) ch^2 (t)dt =4 ∫_0 ^(ln((1/2)+((√5)/2))) ((ch(2t)−1)/2)dt =2 ∫_0 ^(ln(((1+(√5))/2))) (ch(2t)−1)dt =[sh(2t)]_0 ^(ln(((1+(√5))/2))) −2ln(((1+(√5))/2)) =[((e^(2t) −e^(−2t) )/2)]_0 ^(ln(((1+(√5))/2))) −2ln(((1+(√5))/2)) =(1/2){ (((1+(√5))/2))^2 −(((1+(√5))/2))^(−2) }−2ln(((1+(√5))/2))](Q76182.png)
$${let}\:{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{4}+{x}^{\mathrm{2}} }{dx}\:\:{changement}\:{x}=\mathrm{2}{sh}\left({t}\right)\:{give} \\ $$$${I}\:=\int_{\mathrm{0}} ^{{argsh}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} \:\mathrm{2}{ch}\left({t}\right)\mathrm{2}{ch}\left({t}\right){dt}\:=\mathrm{4}\:\int_{\mathrm{0}} ^{{ln}\left(\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}}\right)} {ch}^{\mathrm{2}} \left({t}\right){dt} \\ $$$$=\mathrm{4}\:\int_{\mathrm{0}} ^{{ln}\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\right)} \frac{{ch}\left(\mathrm{2}{t}\right)−\mathrm{1}}{\mathrm{2}}{dt}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{{ln}\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)} \left({ch}\left(\mathrm{2}{t}\right)−\mathrm{1}\right){dt} \\ $$$$=\left[{sh}\left(\mathrm{2}{t}\right)\right]_{\mathrm{0}} ^{{ln}\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)} −\mathrm{2}{ln}\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right) \\ $$$$=\left[\frac{{e}^{\mathrm{2}{t}} −{e}^{−\mathrm{2}{t}} }{\mathrm{2}}\right]_{\mathrm{0}} ^{{ln}\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)} −\mathrm{2}{ln}\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{\:\:\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{−\mathrm{2}} \right\}−\mathrm{2}{ln}\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right) \\ $$
Answered by john santuy last updated on 24/Dec/19
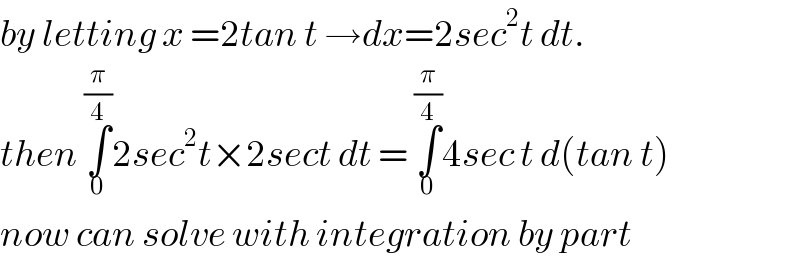
$${by}\:{letting}\:{x}\:=\mathrm{2}{tan}\:{t}\:\rightarrow{dx}=\mathrm{2}{sec}^{\mathrm{2}} {t}\:{dt}.\: \\ $$$${then}\:\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{4}}} {\int}}\mathrm{2}{sec}^{\mathrm{2}} {t}×\mathrm{2}{sect}\:{dt}\:=\:\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{4}}} {\int}}\mathrm{4}{sec}\:{t}\:{d}\left({tan}\:{t}\right) \\ $$$${now}\:{can}\:{solve}\:{with}\:{integration}\:{by}\:{part} \\ $$
Answered by benjo last updated on 24/Dec/19
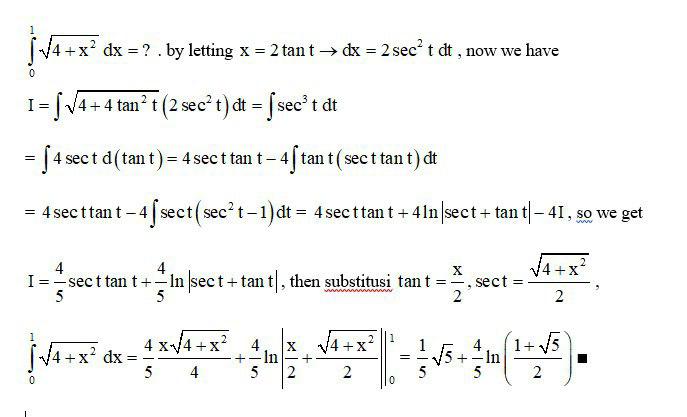
Commented by Master last updated on 24/Dec/19

$$\mathrm{thanks} \\ $$
Commented by benjo last updated on 24/Dec/19

$$\mathrm{okay}\:\mathrm{sir} \\ $$
