Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 76126 by Master last updated on 24/Dec/19

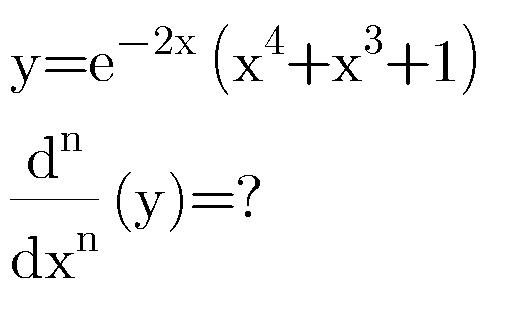
Commented by benjo last updated on 24/Dec/19

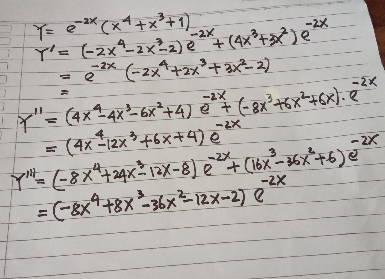
Commented by benjo last updated on 24/Dec/19

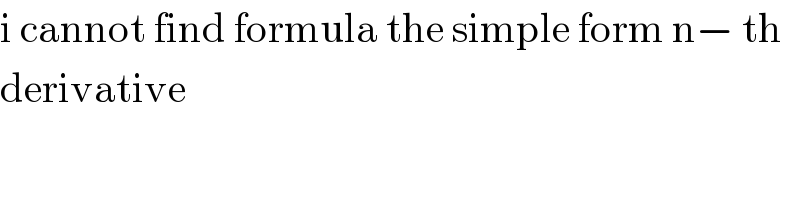
i cannot find formula the simple form n− th derivative

$$\mathrm{i}\:\mathrm{cannot}\:\mathrm{find}\:\mathrm{formula}\:\mathrm{the}\:\mathrm{simple}\:\mathrm{form}\:\mathrm{n}−\:\mathrm{th} \\ $$$$\mathrm{derivative} \\ $$

Commented by Master last updated on 24/Dec/19

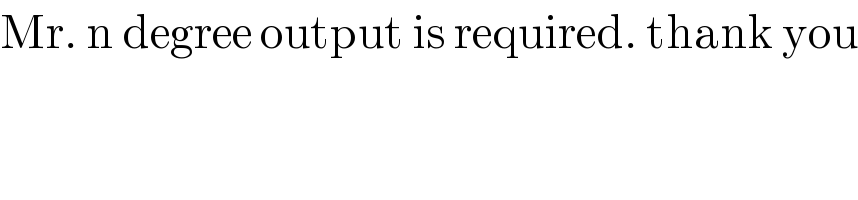
Mr. n degree output is required. thank you

$$\mathrm{Mr}.\:\mathrm{n}\:\mathrm{degree}\:\mathrm{output}\:\mathrm{is}\:\mathrm{required}.\:\mathrm{thank}\:\mathrm{you} \\ $$

Commented by MJS last updated on 24/Dec/19

(d/dx)[y=e^(αx) (ax^4 +bx^3 +cx^2 +dx+e)]= =e^(αx) (aαx^4 +(4a+bα)x^3 +(3b+cα)x^2 +(2c+dα)x+d+eα) it′s possible to find formulas for the constant factors, sorry I have no time right now

$$\frac{{d}}{{dx}}\left[{y}=\mathrm{e}^{\alpha{x}} \left({ax}^{\mathrm{4}} +{bx}^{\mathrm{3}} +{cx}^{\mathrm{2}} +{dx}+{e}\right)\right]= \\ $$$$=\mathrm{e}^{\alpha{x}} \left({a}\alpha{x}^{\mathrm{4}} +\left(\mathrm{4}{a}+{b}\alpha\right){x}^{\mathrm{3}} +\left(\mathrm{3}{b}+{c}\alpha\right){x}^{\mathrm{2}} +\left(\mathrm{2}{c}+{d}\alpha\right){x}+{d}+{e}\alpha\right) \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{possible}\:\mathrm{to}\:\mathrm{find}\:\mathrm{formulas}\:\mathrm{for}\:\mathrm{the}\:\mathrm{constant} \\ $$$$\mathrm{factors},\:\mathrm{sorry}\:\mathrm{I}\:\mathrm{have}\:\mathrm{no}\:\mathrm{time}\:\mathrm{right}\:\mathrm{now} \\ $$

Commented by john santuy last updated on 24/Dec/19

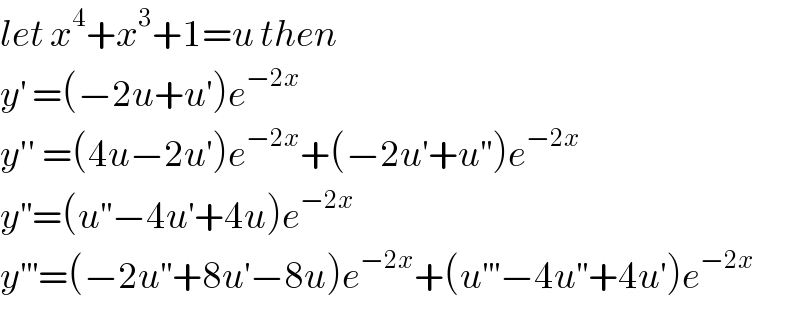
let x^4 +x^3 +1=u then y^′ =(−2u+u^′ )e^(−2x) y′′ =(4u−2u^′ )e^(−2x) +(−2u^′ +u^(′′) )e^(−2x) y^(′′) =(u^(′′) −4u^′ +4u)e^(−2x) y^(′′′) =(−2u^(′′) +8u^′ −8u)e^(−2x) +(u^(′′′) −4u^(′′) +4u^′ )e^(−2x)

$${let}\:{x}^{\mathrm{4}} +{x}^{\mathrm{3}} +\mathrm{1}={u}\:{then}\: \\ $$$${y}^{'} \:=\left(−\mathrm{2}{u}+{u}^{'} \right){e}^{−\mathrm{2}{x}} \\ $$$${y}''\:=\left(\mathrm{4}{u}−\mathrm{2}{u}^{'} \right){e}^{−\mathrm{2}{x}} +\left(−\mathrm{2}{u}^{'} +{u}^{''} \right){e}^{−\mathrm{2}{x}} \\ $$$${y}^{''} =\left({u}^{''} −\mathrm{4}{u}^{'} +\mathrm{4}{u}\right){e}^{−\mathrm{2}{x}} \\ $$$${y}^{'''} =\left(−\mathrm{2}{u}^{''} +\mathrm{8}{u}^{'} −\mathrm{8}{u}\right){e}^{−\mathrm{2}{x}} +\left({u}^{'''} −\mathrm{4}{u}^{''} +\mathrm{4}{u}^{'} \right){e}^{−\mathrm{2}{x}} \\ $$

Commented by john santuy last updated on 24/Dec/19

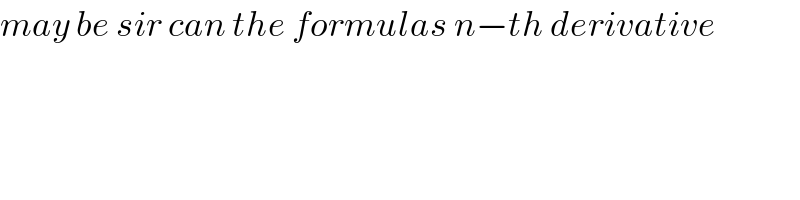
may be sir can the formulas n−th derivative

$${may}\:{be}\:{sir}\:{can}\:{the}\:{formulas}\:{n}−{th}\:{derivative} \\ $$

Commented by mathmax by abdo last updated on 24/Dec/19

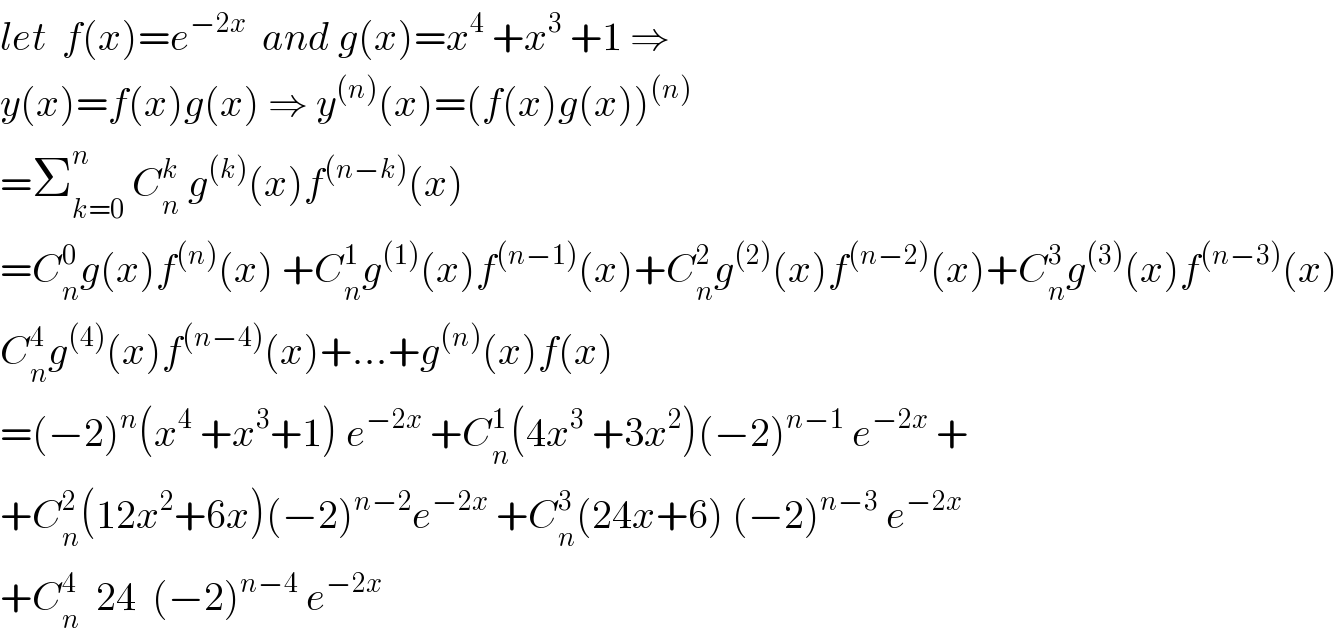
let f(x)=e^(−2x) and g(x)=x^4 +x^3 +1 ⇒ y(x)=f(x)g(x) ⇒ y^((n)) (x)=(f(x)g(x))^((n)) =Σ_(k=0) ^n C_n ^k g^((k)) (x)f^((n−k)) (x) =C_n ^0 g(x)f^((n)) (x) +C_n ^1 g^((1)) (x)f^((n−1)) (x)+C_n ^2 g^((2)) (x)f^((n−2)) (x)+C_n ^3 g^((3)) (x)f^((n−3)) (x) C_n ^4 g^((4)) (x)f^((n−4)) (x)+...+g^((n)) (x)f(x) =(−2)^n (x^4 +x^3 +1) e^(−2x) +C_n ^1 (4x^3 +3x^2 )(−2)^(n−1) e^(−2x) + +C_n ^2 (12x^2 +6x)(−2)^(n−2) e^(−2x) +C_n ^3 (24x+6) (−2)^(n−3) e^(−2x) +C_n ^4 24 (−2)^(n−4) e^(−2x)

$${let}\:\:{f}\left({x}\right)={e}^{−\mathrm{2}{x}} \:\:{and}\:{g}\left({x}\right)={x}^{\mathrm{4}} \:+{x}^{\mathrm{3}} \:+\mathrm{1}\:\Rightarrow \\ $$$${y}\left({x}\right)={f}\left({x}\right){g}\left({x}\right)\:\Rightarrow\:{y}^{\left({n}\right)} \left({x}\right)=\left({f}\left({x}\right){g}\left({x}\right)\right)^{\left({n}\right)} \\ $$$$=\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:{g}^{\left({k}\right)} \left({x}\right){f}^{\left({n}−{k}\right)} \left({x}\right) \\ $$$$={C}_{{n}} ^{\mathrm{0}} {g}\left({x}\right){f}^{\left({n}\right)} \left({x}\right)\:+{C}_{{n}} ^{\mathrm{1}} {g}^{\left(\mathrm{1}\right)} \left({x}\right){f}^{\left({n}−\mathrm{1}\right)} \left({x}\right)+{C}_{{n}} ^{\mathrm{2}} {g}^{\left(\mathrm{2}\right)} \left({x}\right){f}^{\left({n}−\mathrm{2}\right)} \left({x}\right)+{C}_{{n}} ^{\mathrm{3}} {g}^{\left(\mathrm{3}\right)} \left({x}\right){f}^{\left({n}−\mathrm{3}\right)} \left({x}\right) \\ $$$${C}_{{n}} ^{\mathrm{4}} {g}^{\left(\mathrm{4}\right)} \left({x}\right){f}^{\left({n}−\mathrm{4}\right)} \left({x}\right)+...+{g}^{\left({n}\right)} \left({x}\right){f}\left({x}\right) \\ $$$$=\left(−\mathrm{2}\right)^{{n}} \left({x}^{\mathrm{4}} \:+{x}^{\mathrm{3}} +\mathrm{1}\right)\:{e}^{−\mathrm{2}{x}} \:+{C}_{{n}} ^{\mathrm{1}} \left(\mathrm{4}{x}^{\mathrm{3}} \:+\mathrm{3}{x}^{\mathrm{2}} \right)\left(−\mathrm{2}\right)^{{n}−\mathrm{1}} \:{e}^{−\mathrm{2}{x}} \:+ \\ $$$$+{C}_{{n}} ^{\mathrm{2}} \left(\mathrm{12}{x}^{\mathrm{2}} +\mathrm{6}{x}\right)\left(−\mathrm{2}\right)^{{n}−\mathrm{2}} {e}^{−\mathrm{2}{x}} \:+{C}_{{n}} ^{\mathrm{3}} \left(\mathrm{24}{x}+\mathrm{6}\right)\:\left(−\mathrm{2}\right)^{{n}−\mathrm{3}} \:{e}^{−\mathrm{2}{x}} \\ $$$$+{C}_{{n}} ^{\mathrm{4}} \:\:\mathrm{24}\:\:\left(−\mathrm{2}\right)^{{n}−\mathrm{4}} \:{e}^{−\mathrm{2}{x}} \\ $$

Commented by Master last updated on 24/Dec/19

thank you sir

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by turbo msup by abdo last updated on 24/Dec/19

you are welcome.

$${you}\:{are}\:{welcome}. \\ $$

Answered by mr W last updated on 24/Dec/19

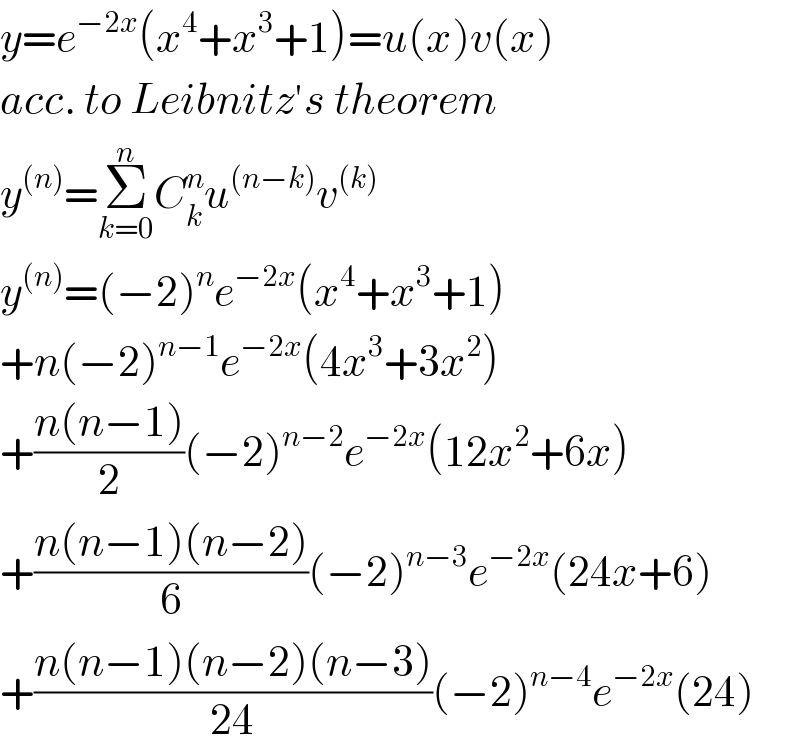
y=e^(−2x) (x^4 +x^3 +1)=u(x)v(x) acc. to Leibnitz′s theorem y^((n)) =Σ_(k=0) ^n C_k ^n u^((n−k)) v^((k)) y^((n)) =(−2)^n e^(−2x) (x^4 +x^3 +1) +n(−2)^(n−1) e^(−2x) (4x^3 +3x^2 ) +((n(n−1))/2)(−2)^(n−2) e^(−2x) (12x^2 +6x) +((n(n−1)(n−2))/6)(−2)^(n−3) e^(−2x) (24x+6) +((n(n−1)(n−2)(n−3))/(24))(−2)^(n−4) e^(−2x) (24)

$${y}={e}^{−\mathrm{2}{x}} \left({x}^{\mathrm{4}} +{x}^{\mathrm{3}} +\mathrm{1}\right)={u}\left({x}\right){v}\left({x}\right) \\ $$$${acc}.\:{to}\:{Leibnitz}'{s}\:{theorem} \\ $$$${y}^{\left({n}\right)} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{C}_{{k}} ^{{n}} {u}^{\left({n}−{k}\right)} {v}^{\left({k}\right)} \\ $$$${y}^{\left({n}\right)} =\left(−\mathrm{2}\right)^{{n}} {e}^{−\mathrm{2}{x}} \left({x}^{\mathrm{4}} +{x}^{\mathrm{3}} +\mathrm{1}\right) \\ $$$$+{n}\left(−\mathrm{2}\right)^{{n}−\mathrm{1}} {e}^{−\mathrm{2}{x}} \left(\mathrm{4}{x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} \right) \\ $$$$+\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}}\left(−\mathrm{2}\right)^{{n}−\mathrm{2}} {e}^{−\mathrm{2}{x}} \left(\mathrm{12}{x}^{\mathrm{2}} +\mathrm{6}{x}\right) \\ $$$$+\frac{{n}\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)}{\mathrm{6}}\left(−\mathrm{2}\right)^{{n}−\mathrm{3}} {e}^{−\mathrm{2}{x}} \left(\mathrm{24}{x}+\mathrm{6}\right) \\ $$$$+\frac{{n}\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)\left({n}−\mathrm{3}\right)}{\mathrm{24}}\left(−\mathrm{2}\right)^{{n}−\mathrm{4}} {e}^{−\mathrm{2}{x}} \left(\mathrm{24}\right) \\ $$

Commented by Master last updated on 24/Dec/19

thanks sir

$$\mathrm{thanks}\:\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com