Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 76122 by benjo last updated on 24/Dec/19

Answered by john santuy last updated on 24/Dec/19

i think this problem not difficult

$${i}\:{think}\:{this}\:{problem}\:{not}\:{difficult} \\ $$

Commented by $@ty@m123 last updated on 24/Dec/19

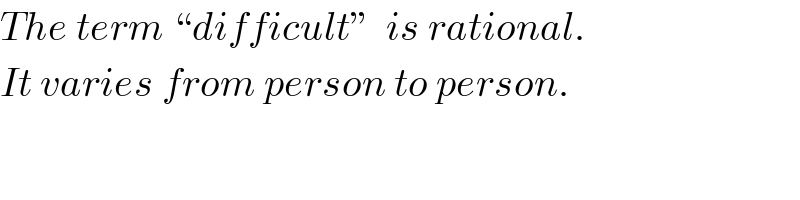
The term “difficult” is rational. It varies from person to person.

$${The}\:{term}\:``{difficult}''\:\:{is}\:{rational}. \\ $$$${It}\:{varies}\:{from}\:{person}\:{to}\:{person}. \\ $$

Commented by john santuy last updated on 24/Dec/19

yes sir. thanks you

$${yes}\:{sir}.\:{thanks}\:{you} \\ $$

Answered by MJS last updated on 24/Dec/19

x+4−(3/(x−4))=2(√((x+4)/(x−4))) ((x^2 −19)/(x−4))=2(√((x+4)/(x−4))) squaring ⇒ not all solutions will fit the given equation (((x^2 −19)/(x−4)))^2 =4((x+4)/(x−4)) (x^2 −19)^2 =4(x^2 −16) x^4 −42x^2 +425=0 x^2 =25∨x^2 =17 ⇒ x=±5∨x=±(√(17)) testing in given equation ⇒ x=5∨x=−(√(17))

$${x}+\mathrm{4}−\frac{\mathrm{3}}{{x}−\mathrm{4}}=\mathrm{2}\sqrt{\frac{{x}+\mathrm{4}}{{x}−\mathrm{4}}} \\ $$$$\frac{{x}^{\mathrm{2}} −\mathrm{19}}{{x}−\mathrm{4}}=\mathrm{2}\sqrt{\frac{{x}+\mathrm{4}}{{x}−\mathrm{4}}} \\ $$$$\mathrm{squaring}\:\Rightarrow\:\mathrm{not}\:\mathrm{all}\:\mathrm{solutions}\:\mathrm{will}\:\mathrm{fit}\:\mathrm{the}\:\mathrm{given} \\ $$$$\mathrm{equation} \\ $$$$\left(\frac{{x}^{\mathrm{2}} −\mathrm{19}}{{x}−\mathrm{4}}\right)^{\mathrm{2}} =\mathrm{4}\frac{{x}+\mathrm{4}}{{x}−\mathrm{4}} \\ $$$$\left({x}^{\mathrm{2}} −\mathrm{19}\right)^{\mathrm{2}} =\mathrm{4}\left({x}^{\mathrm{2}} −\mathrm{16}\right) \\ $$$${x}^{\mathrm{4}} −\mathrm{42}{x}^{\mathrm{2}} +\mathrm{425}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} =\mathrm{25}\vee{x}^{\mathrm{2}} =\mathrm{17} \\ $$$$\Rightarrow\:{x}=\pm\mathrm{5}\vee{x}=\pm\sqrt{\mathrm{17}} \\ $$$$\mathrm{testing}\:\mathrm{in}\:\mathrm{given}\:\mathrm{equation} \\ $$$$\Rightarrow\:{x}=\mathrm{5}\vee{x}=−\sqrt{\mathrm{17}} \\ $$

Commented by benjo last updated on 24/Dec/19

thanks you sir

$$\mathrm{thanks}\:\mathrm{you}\:\mathrm{sir} \\ $$

Answered by behi83417@gmail.com last updated on 24/Dec/19

((x+4)/(x−4))=t^2 ⇒((2x)/8)=((t^2 +1)/(t^2 −1))⇒x=4((t^2 +1)/(t^2 −1)) 4((t^2 +1)/(t^2 −1))+4−2t=(3/(4((t^2 +1)/(t^2 −1))−4))=((3(t^2 −1))/(4(2))) ((8t^2 )/(t^2 −1))−2t=((3(t^2 −1))/8) 64t^2 −16t(t^2 −1)=3(t^2 −1)^2 ⇒3t^4 +16t^3 −70t^2 −16t+3=0 ⇒t=−8.123,−(1/3),+0.123,+3.0 { ((((x+4)/(x−4))=66⇒(x/4)=((67)/(65))⇒x=4.123)),((((x+4)/(x−4))=(1/9)⇒(x/4)=−((10)/8)⇒x=−5.0)),((((x+4)/(x−4))=0.015⇒(x/4)=((1.015)/(0.985))⇒x=−4.123)),((((x+4)/(x−4))=9⇒(x/4)=((10)/8)⇒x=+5.0)) :}

$$\frac{\mathrm{x}+\mathrm{4}}{\mathrm{x}−\mathrm{4}}=\mathrm{t}^{\mathrm{2}} \Rightarrow\frac{\mathrm{2x}}{\mathrm{8}}=\frac{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}\Rightarrow\mathrm{x}=\mathrm{4}\frac{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}{\mathrm{t}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\mathrm{4}\frac{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}+\mathrm{4}−\mathrm{2t}=\frac{\mathrm{3}}{\mathrm{4}\frac{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}−\mathrm{4}}=\frac{\mathrm{3}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)}{\mathrm{4}\left(\mathrm{2}\right)} \\ $$$$\frac{\mathrm{8t}^{\mathrm{2}} }{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}−\mathrm{2t}=\frac{\mathrm{3}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)}{\mathrm{8}} \\ $$$$\mathrm{64t}^{\mathrm{2}} −\mathrm{16t}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{3}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{3t}^{\mathrm{4}} +\mathrm{16t}^{\mathrm{3}} −\mathrm{70t}^{\mathrm{2}} −\mathrm{16t}+\mathrm{3}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{t}=−\mathrm{8}.\mathrm{123},−\frac{\mathrm{1}}{\mathrm{3}},+\mathrm{0}.\mathrm{123},+\mathrm{3}.\mathrm{0} \\ $$$$\begin{cases}{\frac{\mathrm{x}+\mathrm{4}}{\mathrm{x}−\mathrm{4}}=\mathrm{66}\Rightarrow\frac{\mathrm{x}}{\mathrm{4}}=\frac{\mathrm{67}}{\mathrm{65}}\Rightarrow\mathrm{x}=\mathrm{4}.\mathrm{123}}\\{\frac{\mathrm{x}+\mathrm{4}}{\mathrm{x}−\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{9}}\Rightarrow\frac{\mathrm{x}}{\mathrm{4}}=−\frac{\mathrm{10}}{\mathrm{8}}\Rightarrow\mathrm{x}=−\mathrm{5}.\mathrm{0}}\\{\frac{\mathrm{x}+\mathrm{4}}{\mathrm{x}−\mathrm{4}}=\mathrm{0}.\mathrm{015}\Rightarrow\frac{\mathrm{x}}{\mathrm{4}}=\frac{\mathrm{1}.\mathrm{015}}{\mathrm{0}.\mathrm{985}}\Rightarrow\mathrm{x}=−\mathrm{4}.\mathrm{123}}\\{\frac{\mathrm{x}+\mathrm{4}}{\mathrm{x}−\mathrm{4}}=\mathrm{9}\Rightarrow\frac{\mathrm{x}}{\mathrm{4}}=\frac{\mathrm{10}}{\mathrm{8}}\Rightarrow\mathrm{x}=+\mathrm{5}.\mathrm{0}}\end{cases} \\ $$

Answered by mind is power last updated on 24/Dec/19

⇒1−(2/(√((x+4)(x−4))))=(3/((x−4)(x+4))),x>0≠4 x<0,x≠−4 ⇒1+(2/(√((x−4)(x+4))))=(3/((4+x)(x−4))), Z=(1/(√((x−4)(x+4)))) Quadratique

$$\Rightarrow\mathrm{1}−\frac{\mathrm{2}}{\sqrt{\left(\mathrm{x}+\mathrm{4}\right)\left(\mathrm{x}−\mathrm{4}\right)}}=\frac{\mathrm{3}}{\left(\mathrm{x}−\mathrm{4}\right)\left(\mathrm{x}+\mathrm{4}\right)},\mathrm{x}>\mathrm{0}\neq\mathrm{4} \\ $$$$\mathrm{x}<\mathrm{0},\mathrm{x}\neq−\mathrm{4} \\ $$$$\Rightarrow\mathrm{1}+\frac{\mathrm{2}}{\sqrt{\left(\mathrm{x}−\mathrm{4}\right)\left(\mathrm{x}+\mathrm{4}\right)}}=\frac{\mathrm{3}}{\left(\mathrm{4}+\mathrm{x}\right)\left(\mathrm{x}−\mathrm{4}\right)},\:\:\mathrm{Z}=\frac{\mathrm{1}}{\sqrt{\left(\mathrm{x}−\mathrm{4}\right)\left(\mathrm{x}+\mathrm{4}\right)}} \\ $$$$\mathrm{Quadratique} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com