
Question Number 76090 by john santuy last updated on 23/Dec/19
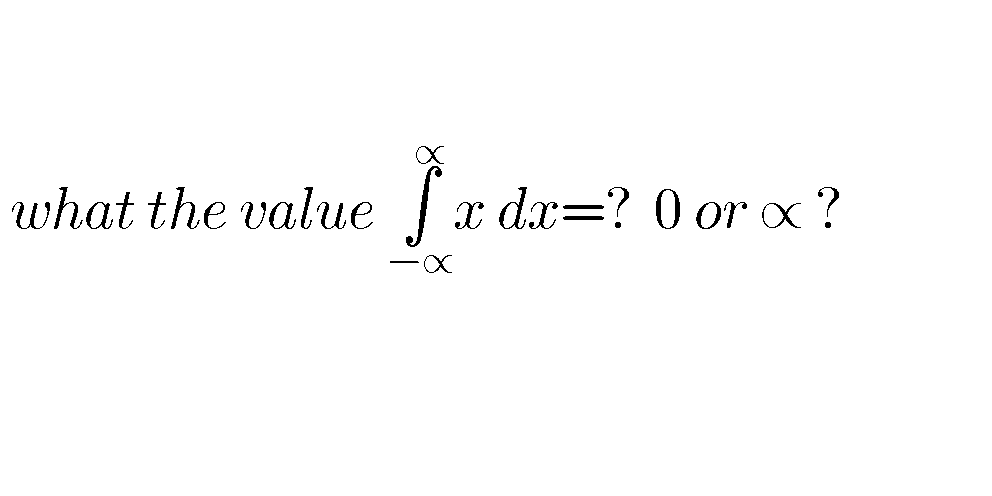
Commented by Prithwish sen last updated on 23/Dec/19

$$\mathrm{0} \\ $$
Answered by MJS last updated on 23/Dec/19
![we had this before ∫_(−a) ^a xdx=[(x^2 /2)]_(−a) ^a =0 ∀a∈R ⇒ lim_(a→∞) (∫_(−a) ^a xdx)=0](Q76102.png)
$$\mathrm{we}\:\mathrm{had}\:\mathrm{this}\:\mathrm{before} \\ $$$$\underset{−{a}} {\overset{{a}} {\int}}{xdx}=\left[\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right]_{−{a}} ^{{a}} =\mathrm{0}\:\forall{a}\in\mathbb{R} \\ $$$$\Rightarrow\:\underset{{a}\rightarrow\infty} {\mathrm{lim}}\left(\underset{−{a}} {\overset{{a}} {\int}}{xdx}\right)=\mathrm{0} \\ $$
Commented by Prithwish sen last updated on 23/Dec/19
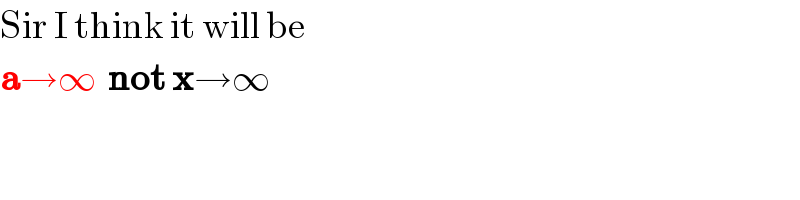
$$\mathrm{Sir}\:\mathrm{I}\:\mathrm{think}\:\mathrm{it}\:\mathrm{will}\:\mathrm{be} \\ $$$$\boldsymbol{\mathrm{a}}\rightarrow\infty\:\:\boldsymbol{\mathrm{not}}\:\boldsymbol{\mathrm{x}}\rightarrow\infty \\ $$
Commented by MJS last updated on 23/Dec/19
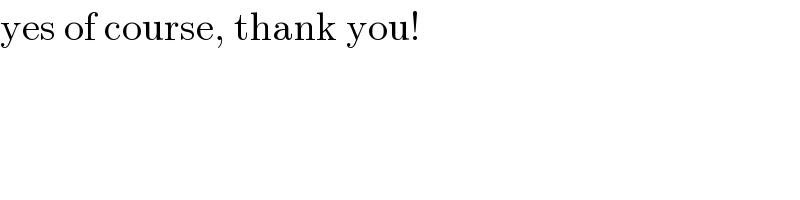
$$\mathrm{yes}\:\mathrm{of}\:\mathrm{course},\:\mathrm{thank}\:\mathrm{you}! \\ $$
Commented by Prithwish sen last updated on 23/Dec/19

$$\mathrm{welcome}\:\mathrm{sir}. \\ $$
