
Question Number 74068 by FCB last updated on 18/Nov/19
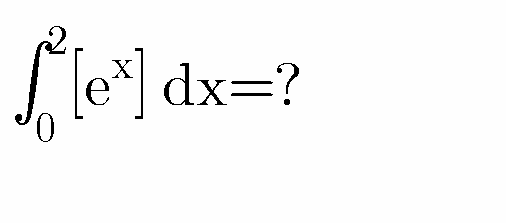
Commented by FCB last updated on 19/Nov/19

$$\mathrm{thank}\:\mathrm{you} \\ $$
Commented by FCB last updated on 18/Nov/19
![[e^x ]−Integerpart(whole part)](Q74069.png)
$$\left[\mathrm{e}^{\mathrm{x}} \right]−\mathrm{Integerpart}\left(\mathrm{whole}\:\mathrm{part}\right) \\ $$
Commented by mathmax by abdo last updated on 18/Nov/19
![changement e^x =t give ∫_0 ^2 [e^x ]dx = ∫_1 ^e^2 [t](dt/t) e^2 ∼7,389 ⇒∫_0 ^2 [e^x ]dx =∫_1 ^(7,389) (([t])/t)dt =Σ_(k=1) ^6 ∫_k ^(k+1) (([t])/t)dt + ∫_7 ^(7,389) (([t])/t)dt =Σ_(k=1) ^6 k {ln(k+1)−ln(k)} +7 {ln(e^2 )−ln(7)} =Σ_(k=1) ^6 kln(((k+1)/k)) +7{2−ln(7)} =ln(2)+2ln((3/2))+3ln((4/3))+4ln((5/4))+5ln((6/5))+6ln((7/6)) +7{2−ln(7)}.](Q74096.png)
$${changement}\:\:{e}^{{x}} ={t}\:{give}\:\int_{\mathrm{0}} ^{\mathrm{2}} \left[{e}^{{x}} \right]{dx}\:=\:\int_{\mathrm{1}} ^{{e}^{\mathrm{2}} } \left[{t}\right]\frac{{dt}}{{t}} \\ $$$${e}^{\mathrm{2}} \sim\mathrm{7},\mathrm{389}\:\Rightarrow\int_{\mathrm{0}} ^{\mathrm{2}} \left[{e}^{{x}} \right]{dx}\:=\int_{\mathrm{1}} ^{\mathrm{7},\mathrm{389}} \:\frac{\left[{t}\right]}{{t}}{dt} \\ $$$$=\sum_{{k}=\mathrm{1}} ^{\mathrm{6}} \:\:\int_{{k}} ^{{k}+\mathrm{1}} \:\:\frac{\left[{t}\right]}{{t}}{dt}\:+\:\int_{\mathrm{7}} ^{\mathrm{7},\mathrm{389}} \:\frac{\left[{t}\right]}{{t}}{dt} \\ $$$$=\sum_{{k}=\mathrm{1}} ^{\mathrm{6}} {k}\:\left\{{ln}\left({k}+\mathrm{1}\right)−{ln}\left({k}\right)\right\}\:+\mathrm{7}\:\left\{{ln}\left({e}^{\mathrm{2}} \right)−{ln}\left(\mathrm{7}\right)\right\} \\ $$$$=\sum_{{k}=\mathrm{1}} ^{\mathrm{6}} {kln}\left(\frac{{k}+\mathrm{1}}{{k}}\right)\:+\mathrm{7}\left\{\mathrm{2}−{ln}\left(\mathrm{7}\right)\right\} \\ $$$$={ln}\left(\mathrm{2}\right)+\mathrm{2}{ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)+\mathrm{3}{ln}\left(\frac{\mathrm{4}}{\mathrm{3}}\right)+\mathrm{4}{ln}\left(\frac{\mathrm{5}}{\mathrm{4}}\right)+\mathrm{5}{ln}\left(\frac{\mathrm{6}}{\mathrm{5}}\right)+\mathrm{6}{ln}\left(\frac{\mathrm{7}}{\mathrm{6}}\right) \\ $$$$+\mathrm{7}\left\{\mathrm{2}−{ln}\left(\mathrm{7}\right)\right\}. \\ $$
Commented by abdomathmax last updated on 19/Nov/19
$${you}\:{are}\:{welcome}. \\ $$
Answered by Tanmay chaudhury last updated on 18/Nov/19
![e^x =1 when x=0 e^x =2 when x=ln2 e^x =3 when x=ln3 e^x =4 when x=ln4 e^x =5 when x=ln5 e^x =6 when x=ln6 e^x =7 when x=ln7 e^x =8 when x=ln8→x=2.079 beyond given interval ∫_0 ^2 [e^x ]dx =∫_0 ^(ln2) 1×dx+∫_(ln2) ^(ln3) 2dx+∫_(ln3) ^(ln4) 3dx+∫_(ln4) ^(ln5) 4dx+∫_(ln5) ^(ln6) 5dx+∫_(ln6) ^(ln7) 6dx= ln2+2(ln3−ln2)+3(ln4−ln3)+4(ln5−ln4)+5(ln6−ln5)+6(ln7−ln6) =−ln2−ln3−ln4−ln5−ln6+6ln7 =ln((7^6 /(2×3×4×5×6)))=ln((7^6 /(720)))=6ln7−ln720 =11.68−6.58≈5.10 pls check...](Q74080.png)
$${e}^{{x}} =\mathrm{1}\:\:{when}\:{x}=\mathrm{0} \\ $$$${e}^{{x}} =\mathrm{2}\:\:{when}\:{x}={ln}\mathrm{2} \\ $$$${e}^{{x}} =\mathrm{3}\:\:\:{when}\:{x}={ln}\mathrm{3} \\ $$$${e}^{{x}} =\mathrm{4}\:\:\:{when}\:{x}={ln}\mathrm{4} \\ $$$${e}^{{x}} =\mathrm{5}\:\:{when}\:{x}={ln}\mathrm{5} \\ $$$${e}^{{x}} =\mathrm{6}\:{when}\:{x}={ln}\mathrm{6} \\ $$$${e}^{{x}} =\mathrm{7}\:\:{when}\:{x}={ln}\mathrm{7} \\ $$$${e}^{{x}} =\mathrm{8}\:\:{when}\:{x}={ln}\mathrm{8}\rightarrow{x}=\mathrm{2}.\mathrm{079}\:{beyond}\:{given}\:{interval} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}} \left[{e}^{{x}} \right]{dx} \\ $$$$=\int_{\mathrm{0}} ^{{ln}\mathrm{2}} \mathrm{1}×{dx}+\int_{{ln}\mathrm{2}} ^{{ln}\mathrm{3}} \mathrm{2}{dx}+\int_{{ln}\mathrm{3}} ^{{ln}\mathrm{4}} \mathrm{3}{dx}+\int_{{ln}\mathrm{4}} ^{{ln}\mathrm{5}} \mathrm{4}{dx}+\int_{{ln}\mathrm{5}} ^{{ln}\mathrm{6}} \mathrm{5}{dx}+\int_{{ln}\mathrm{6}} ^{{ln}\mathrm{7}} \mathrm{6}{dx}= \\ $$$${ln}\mathrm{2}+\mathrm{2}\left({ln}\mathrm{3}−{ln}\mathrm{2}\right)+\mathrm{3}\left({ln}\mathrm{4}−{ln}\mathrm{3}\right)+\mathrm{4}\left({ln}\mathrm{5}−{ln}\mathrm{4}\right)+\mathrm{5}\left({ln}\mathrm{6}−{ln}\mathrm{5}\right)+\mathrm{6}\left({ln}\mathrm{7}−{ln}\mathrm{6}\right) \\ $$$$=−{ln}\mathrm{2}−{ln}\mathrm{3}−{ln}\mathrm{4}−{ln}\mathrm{5}−{ln}\mathrm{6}+\mathrm{6}{ln}\mathrm{7} \\ $$$$={ln}\left(\frac{\mathrm{7}^{\mathrm{6}} }{\mathrm{2}×\mathrm{3}×\mathrm{4}×\mathrm{5}×\mathrm{6}}\right)={ln}\left(\frac{\mathrm{7}^{\mathrm{6}} }{\mathrm{720}}\right)=\mathrm{6}{ln}\mathrm{7}−{ln}\mathrm{720} \\ $$$$=\mathrm{11}.\mathrm{68}−\mathrm{6}.\mathrm{58}\approx\mathrm{5}.\mathrm{10}\:\:{pls}\:{check}... \\ $$
Commented by mr W last updated on 19/Nov/19
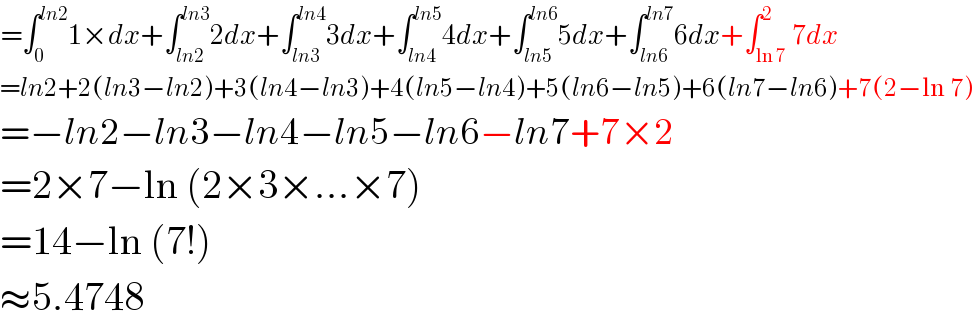
$$=\int_{\mathrm{0}} ^{{ln}\mathrm{2}} \mathrm{1}×{dx}+\int_{{ln}\mathrm{2}} ^{{ln}\mathrm{3}} \mathrm{2}{dx}+\int_{{ln}\mathrm{3}} ^{{ln}\mathrm{4}} \mathrm{3}{dx}+\int_{{ln}\mathrm{4}} ^{{ln}\mathrm{5}} \mathrm{4}{dx}+\int_{{ln}\mathrm{5}} ^{{ln}\mathrm{6}} \mathrm{5}{dx}+\int_{{ln}\mathrm{6}} ^{{ln}\mathrm{7}} \mathrm{6}{dx}+\int_{\mathrm{ln}\:\mathrm{7}} ^{\mathrm{2}} \mathrm{7}{dx} \\ $$$$={ln}\mathrm{2}+\mathrm{2}\left({ln}\mathrm{3}−{ln}\mathrm{2}\right)+\mathrm{3}\left({ln}\mathrm{4}−{ln}\mathrm{3}\right)+\mathrm{4}\left({ln}\mathrm{5}−{ln}\mathrm{4}\right)+\mathrm{5}\left({ln}\mathrm{6}−{ln}\mathrm{5}\right)+\mathrm{6}\left({ln}\mathrm{7}−{ln}\mathrm{6}\right)+\mathrm{7}\left(\mathrm{2}−\mathrm{ln}\:\mathrm{7}\right) \\ $$$$=−{ln}\mathrm{2}−{ln}\mathrm{3}−{ln}\mathrm{4}−{ln}\mathrm{5}−{ln}\mathrm{6}−{ln}\mathrm{7}+\mathrm{7}×\mathrm{2} \\ $$$$=\mathrm{2}×\mathrm{7}−\mathrm{ln}\:\left(\mathrm{2}×\mathrm{3}×...×\mathrm{7}\right) \\ $$$$=\mathrm{14}−\mathrm{ln}\:\left(\mathrm{7}!\right) \\ $$$$\approx\mathrm{5}.\mathrm{4748} \\ $$
Commented by FCB last updated on 18/Nov/19

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
