Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 73030 by Tanmay chaudhury last updated on 05/Nov/19

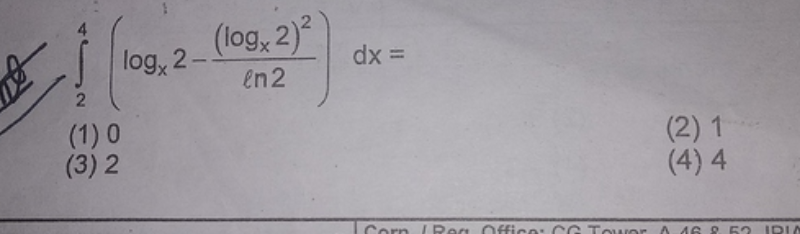
Answered by Tanmay chaudhury last updated on 05/Nov/19

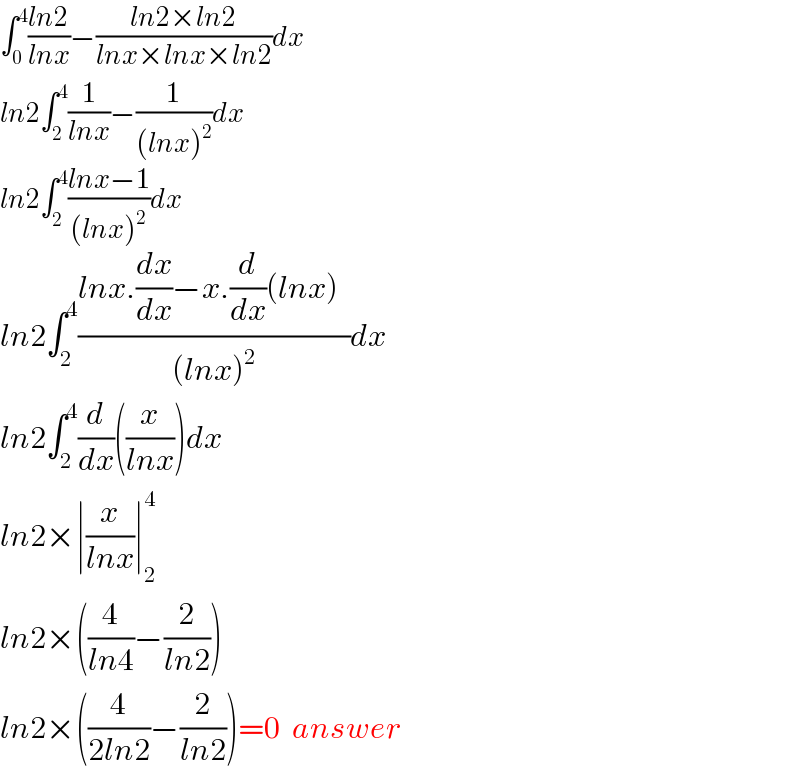
∫_0 ^4 ((ln2)/(lnx))−((ln2×ln2)/(lnx×lnx×ln2))dx ln2∫_2 ^4 (1/(lnx))−(1/((lnx)^2 ))dx ln2∫_2 ^4 ((lnx−1)/((lnx)^2 ))dx ln2∫_2 ^4 ((lnx.(dx/dx)−x.(d/dx)(lnx) )/((lnx)^2 ))dx^ ln2∫_2 ^4 (d/dx)((x/(lnx)))dx ln2×∣(x/(lnx))∣_2 ^4 ln2×((4/(ln4))−(2/(ln2))) ln2×((4/(2ln2))−(2/(ln2)))=0 answer

$$\int_{\mathrm{0}} ^{\mathrm{4}} \frac{{ln}\mathrm{2}}{{lnx}}−\frac{{ln}\mathrm{2}×{ln}\mathrm{2}}{{lnx}×{lnx}×{ln}\mathrm{2}}{dx} \\ $$$${ln}\mathrm{2}\int_{\mathrm{2}} ^{\mathrm{4}} \frac{\mathrm{1}}{{lnx}}−\frac{\mathrm{1}}{\left({lnx}\right)^{\mathrm{2}} }{dx} \\ $$$${ln}\mathrm{2}\int_{\mathrm{2}} ^{\mathrm{4}} \frac{{lnx}−\mathrm{1}}{\left({lnx}\right)^{\mathrm{2}} }{dx} \\ $$$${ln}\mathrm{2}\int_{\mathrm{2}} ^{\mathrm{4}} \frac{{lnx}.\frac{{dx}}{{dx}}−{x}.\frac{{d}}{{dx}}\left({lnx}\right)\:\:}{\left({lnx}\right)^{\mathrm{2}} }{d}\overset{} {{x}} \\ $$$${ln}\mathrm{2}\int_{\mathrm{2}} ^{\mathrm{4}} \frac{{d}}{{dx}}\left(\frac{{x}}{{lnx}}\right){dx}\: \\ $$$${ln}\mathrm{2}×\mid\frac{{x}}{{lnx}}\mid_{\mathrm{2}} ^{\mathrm{4}} \\ $$$${ln}\mathrm{2}×\left(\frac{\mathrm{4}}{{ln}\mathrm{4}}−\frac{\mathrm{2}}{{ln}\mathrm{2}}\right) \\ $$$${ln}\mathrm{2}×\left(\frac{\mathrm{4}}{\mathrm{2}{ln}\mathrm{2}}−\frac{\mathrm{2}}{{ln}\mathrm{2}}\right)=\mathrm{0}\:\:{answer} \\ $$

Answered by mind is power last updated on 05/Nov/19

∫_2 ^4 (log_x (2)−(((log_x (2))^2 )/(ln(2))))dx =∫((ln(2))/(ln(x)))−((ln(2))/(ln^2 (x)))dx =ln(2)∫((ln(x)−1)/(ln^2 (x)))dx =ln(2)∫d((x/(ln(x))))=ln2[(x/(ln(x)))]_2 ^4 =((4ln(2))/(ln(4)))−((2ln(2))/(ln(2)))=2−2=0

$$\int_{\mathrm{2}} ^{\mathrm{4}} \left(\mathrm{log}_{\mathrm{x}} \left(\mathrm{2}\right)−\frac{\left(\mathrm{log}_{\mathrm{x}} \left(\mathrm{2}\right)\right)^{\mathrm{2}} }{\mathrm{ln}\left(\mathrm{2}\right)}\right)\mathrm{dx} \\ $$$$=\int\frac{\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{ln}\left(\mathrm{x}\right)}−\frac{\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{x}\right)}\mathrm{dx} \\ $$$$=\mathrm{ln}\left(\mathrm{2}\right)\int\frac{\mathrm{ln}\left(\mathrm{x}\right)−\mathrm{1}}{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{x}\right)}\mathrm{dx} \\ $$$$=\mathrm{ln}\left(\mathrm{2}\right)\int\mathrm{d}\left(\frac{\mathrm{x}}{\mathrm{ln}\left(\mathrm{x}\right)}\right)=\mathrm{ln2}\left[\frac{\mathrm{x}}{\mathrm{ln}\left(\mathrm{x}\right)}\right]_{\mathrm{2}} ^{\mathrm{4}} =\frac{\mathrm{4ln}\left(\mathrm{2}\right)}{\mathrm{ln}\left(\mathrm{4}\right)}−\frac{\mathrm{2ln}\left(\mathrm{2}\right)}{\mathrm{ln}\left(\mathrm{2}\right)}=\mathrm{2}−\mathrm{2}=\mathrm{0} \\ $$

Commented by Tanmay chaudhury last updated on 05/Nov/19

thank you sir...

$${thank}\:{you}\:{sir}... \\ $$

Commented by mind is power last updated on 05/Nov/19

y′re welcom

$$\mathrm{y}'\mathrm{re}\:\mathrm{welcom} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com