Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 7178 by aftab ahmad last updated on 14/Aug/16

Commented by aftab ahmad last updated on 14/Aug/16

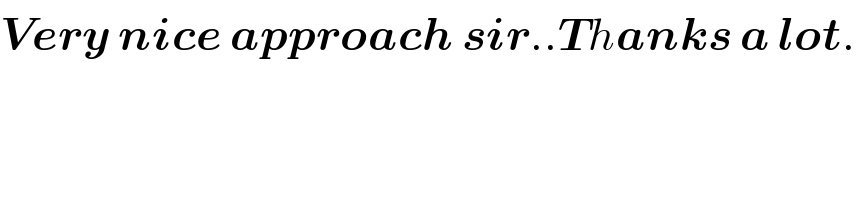
Very nice approach sir..Thanks a lot.

$$\boldsymbol{{Very}}\:\boldsymbol{{nice}}\:\boldsymbol{{approach}}\:\boldsymbol{{sir}}..\boldsymbol{{T}}{h}\boldsymbol{{anks}}\:\boldsymbol{{a}}\:\boldsymbol{{lot}}. \\ $$

Commented by Yozzia last updated on 14/Aug/16

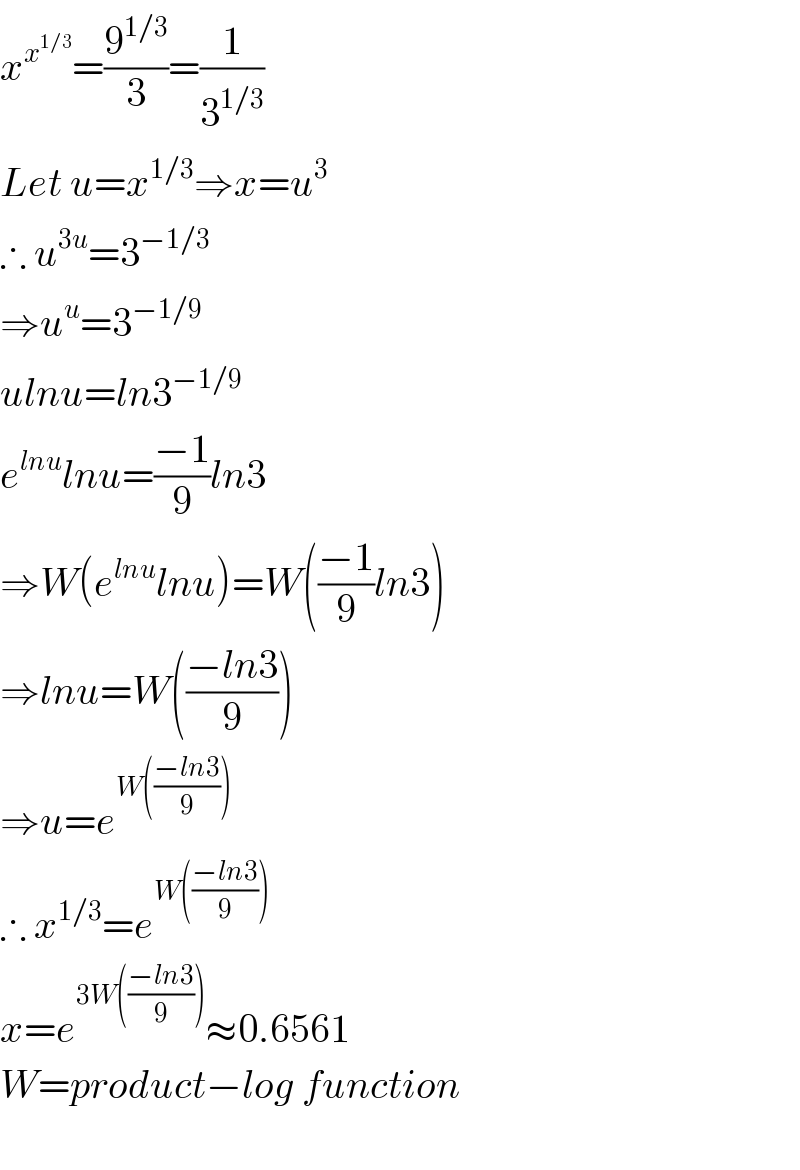
x^x^(1/3) =(9^(1/3) /3)=(1/3^(1/3) ) Let u=x^(1/3) ⇒x=u^3 ∴ u^(3u) =3^(−1/3) ⇒u^u =3^(−1/9) ulnu=ln3^(−1/9) e^(lnu) lnu=((−1)/9)ln3 ⇒W(e^(lnu) lnu)=W(((−1)/9)ln3) ⇒lnu=W(((−ln3)/9)) ⇒u=e^(W(((−ln3)/9))) ∴ x^(1/3) =e^(W(((−ln3)/9))) x=e^(3W(((−ln3)/9))) ≈0.6561 W=product−log function

$${x}^{{x}^{\mathrm{1}/\mathrm{3}} } =\frac{\mathrm{9}^{\mathrm{1}/\mathrm{3}} }{\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{1}/\mathrm{3}} } \\ $$$${Let}\:{u}={x}^{\mathrm{1}/\mathrm{3}} \Rightarrow{x}={u}^{\mathrm{3}} \\ $$$$\therefore\:{u}^{\mathrm{3}{u}} =\mathrm{3}^{−\mathrm{1}/\mathrm{3}} \\ $$$$\Rightarrow{u}^{{u}} =\mathrm{3}^{−\mathrm{1}/\mathrm{9}} \\ $$$${ulnu}={ln}\mathrm{3}^{−\mathrm{1}/\mathrm{9}} \\ $$$${e}^{{lnu}} {lnu}=\frac{−\mathrm{1}}{\mathrm{9}}{ln}\mathrm{3} \\ $$$$\Rightarrow{W}\left({e}^{{lnu}} {lnu}\right)={W}\left(\frac{−\mathrm{1}}{\mathrm{9}}{ln}\mathrm{3}\right) \\ $$$$\Rightarrow{lnu}={W}\left(\frac{−{ln}\mathrm{3}}{\mathrm{9}}\right) \\ $$$$\Rightarrow{u}={e}^{{W}\left(\frac{−{ln}\mathrm{3}}{\mathrm{9}}\right)} \\ $$$$\therefore\:{x}^{\mathrm{1}/\mathrm{3}} ={e}^{{W}\left(\frac{−{ln}\mathrm{3}}{\mathrm{9}}\right)} \\ $$$${x}={e}^{\mathrm{3}{W}\left(\frac{−{ln}\mathrm{3}}{\mathrm{9}}\right)} \approx\mathrm{0}.\mathrm{6561} \\ $$$${W}={product}−{log}\:{function} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com