
Question Number 71348 by ajfour last updated on 13/Oct/19
Commented by ajfour last updated on 13/Oct/19

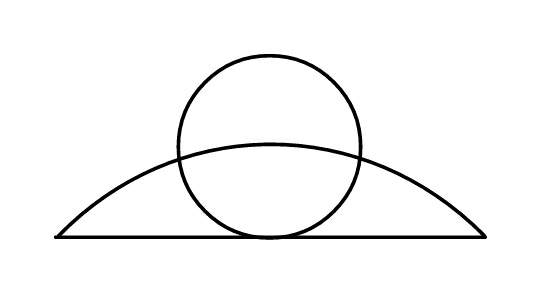
$${If}\:{the}\:{circle}\:{has}\:{unit}\:{radius}\:{and} \\ $$$${each}\:{part}\:{have}\:{same}\:{area},\:{find} \\ $$$${radius}\:{of}\:{circular}\:{arc}. \\ $$
Commented by ajfour last updated on 14/Oct/19
Commented by ajfour last updated on 14/Oct/19
![let center of small circle be origin. p^2 +q^2 =1 p^2 +(q+1+k)^2 =R^2 ⇒ (1+k)(2q+1+k)=R^2 −1 ⇒ q=(1/2)[((R^2 −1)/(1+k))−(1+k)] < 0 ⇒ p=(√(1−(1/4)[((R^2 −1)/(1+k))−(1+k)]^2 )) let θ=tan^(−1) ((∣q∣)/p) A_1 =(((π/2−θ))/2) ; let β=tan^(−1) (p/(q+1+k)) A_2 =((R^2 β)/2) & A_3 =((p(1+k))/2) Now A_1 −(A_2 −A_3 )=(π/4) ⇒ (((π/2−θ))/2)−((R^2 β)/2)+((p(1+k))/2)=(π/4) A_4 =(R^2 /2)cos^(−1) (k/R)−((k(√(R^2 −k^2 )))/2)=(π/2) θ=tan^(−1) (((−(1/2)[((R^2 −1)/(1+k))−(1+k)])/(√(1−(1/4)[((R^2 −1)/(1+k))−(1+k)]^2 )))) β=tan^(−1) (p/(q+1+k)) __________________________.](Q71369.png)
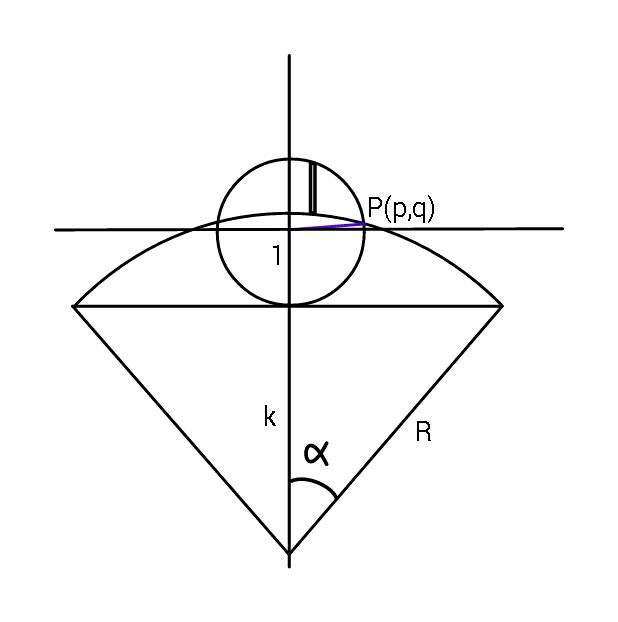
$${let}\:{center}\:{of}\:{small}\:{circle}\:{be}\:{origin}. \\ $$$${p}^{\mathrm{2}} +{q}^{\mathrm{2}} =\mathrm{1} \\ $$$${p}^{\mathrm{2}} +\left({q}+\mathrm{1}+{k}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$$\Rightarrow\:\left(\mathrm{1}+{k}\right)\left(\mathrm{2}{q}+\mathrm{1}+{k}\right)={R}^{\mathrm{2}} −\mathrm{1} \\ $$$$\Rightarrow\:{q}=\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{{R}^{\mathrm{2}} −\mathrm{1}}{\mathrm{1}+{k}}−\left(\mathrm{1}+{k}\right)\right]\:\:\:<\:\mathrm{0} \\ $$$$\Rightarrow\:\:{p}=\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}\left[\frac{{R}^{\mathrm{2}} −\mathrm{1}}{\mathrm{1}+{k}}−\left(\mathrm{1}+{k}\right)\right]^{\mathrm{2}} } \\ $$$${let}\:\:\:\theta=\mathrm{tan}^{−\mathrm{1}} \frac{\mid{q}\mid}{{p}} \\ $$$$\:\:{A}_{\mathrm{1}} =\frac{\left(\pi/\mathrm{2}−\theta\right)}{\mathrm{2}}\:\:;\: \\ $$$${let}\:\:\beta=\mathrm{tan}^{−\mathrm{1}} \frac{{p}}{{q}+\mathrm{1}+{k}} \\ $$$${A}_{\mathrm{2}} =\frac{{R}^{\mathrm{2}} \beta}{\mathrm{2}}\:\:\&\:\:\:{A}_{\mathrm{3}} =\frac{{p}\left(\mathrm{1}+{k}\right)}{\mathrm{2}} \\ $$$${Now}\:\:\:{A}_{\mathrm{1}} −\left({A}_{\mathrm{2}} −{A}_{\mathrm{3}} \right)=\frac{\pi}{\mathrm{4}}\:\:\Rightarrow \\ $$$$\:\frac{\left(\pi/\mathrm{2}−\theta\right)}{\mathrm{2}}−\frac{{R}^{\mathrm{2}} \beta}{\mathrm{2}}+\frac{{p}\left(\mathrm{1}+{k}\right)}{\mathrm{2}}=\frac{\pi}{\mathrm{4}} \\ $$$$\:{A}_{\mathrm{4}} =\frac{{R}^{\mathrm{2}} }{\mathrm{2}}\mathrm{cos}^{−\mathrm{1}} \frac{{k}}{{R}}−\frac{{k}\sqrt{{R}^{\mathrm{2}} −{k}^{\mathrm{2}} }}{\mathrm{2}}=\frac{\pi}{\mathrm{2}} \\ $$$$\:\:\theta=\mathrm{tan}^{−\mathrm{1}} \left(\frac{−\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{{R}^{\mathrm{2}} −\mathrm{1}}{\mathrm{1}+{k}}−\left(\mathrm{1}+{k}\right)\right]}{\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}\left[\frac{{R}^{\mathrm{2}} −\mathrm{1}}{\mathrm{1}+{k}}−\left(\mathrm{1}+{k}\right)\right]^{\mathrm{2}} }}\right) \\ $$$$\:\:\beta=\mathrm{tan}^{−\mathrm{1}} \frac{{p}}{{q}+\mathrm{1}+{k}} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_. \\ $$
