
Question Number 71115 by TawaTawa last updated on 11/Oct/19

Answered by mind is power last updated on 11/Oct/19

$$\mathrm{A}.\left(\mathrm{999994}\right)......\left(\mathrm{1000002}\right)=\mathrm{1}\left(\mathrm{1000003}\right) \\ $$$$\mathrm{used}\:\mathrm{wilson}\:\mathrm{theorem}\:\left(\mathrm{p}−\mathrm{1}\right)!=\mathrm{1}\left(\mathrm{p}\right) \\ $$$$\Rightarrow \\ $$$$\Rightarrow\mathrm{A}\left(−\mathrm{1}\right).\left(−\mathrm{2}\right)......\left(−\mathrm{9}\right)=\mathrm{1}\left(\mathrm{1000003}\right) \\ $$$$\mathrm{A}.\left(\mathrm{9}!\right)=\mathrm{1}\left(\mathrm{1000003}\right) \\ $$$$\mathrm{A}.\mathrm{637123}=\mathrm{1}\left(\mathrm{1000003}\right) \\ $$$$\mathrm{use}\:\mathrm{division}\:\mathrm{to}\:\mathrm{find}\:\mathrm{invers}\:\mathrm{a}\:\mathrm{of}\:\mathrm{637123}\:\mathrm{mod}\left(\mathrm{1000003}\right) \\ $$$$\mathrm{A}=\mathrm{a}\left(\mathrm{1000003}\right) \\ $$$$ \\ $$
Commented by TawaTawa last updated on 11/Oct/19
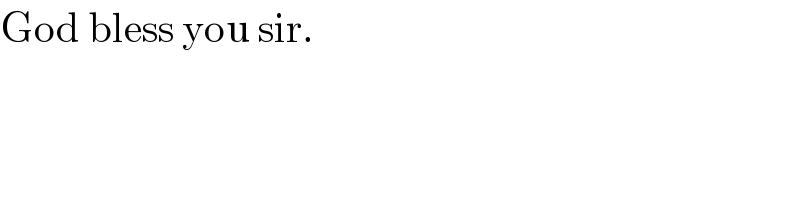
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by TawaTawa last updated on 11/Oct/19
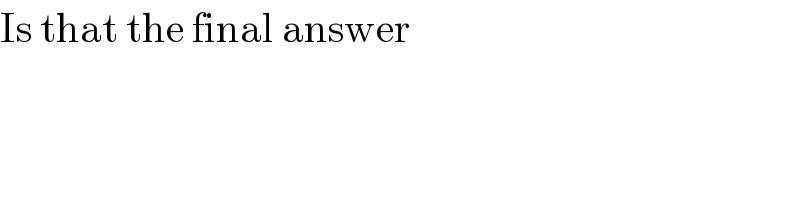
$$\mathrm{Is}\:\mathrm{that}\:\mathrm{the}\:\mathrm{final}\:\mathrm{answer} \\ $$
Commented by mind is power last updated on 12/Oct/19
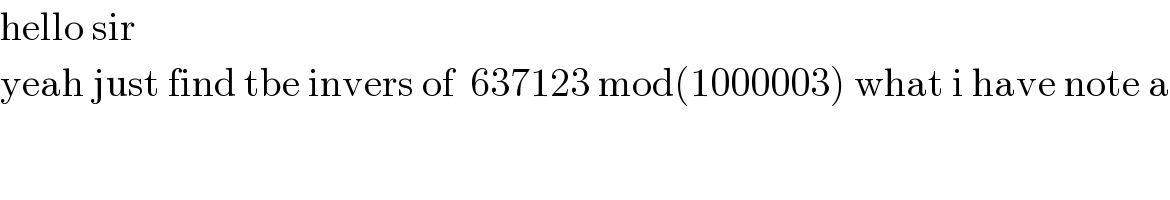
$$\mathrm{hello}\:\mathrm{sir}\: \\ $$$$\mathrm{yeah}\:\mathrm{just}\:\mathrm{find}\:\mathrm{tbe}\:\mathrm{invers}\:\mathrm{of}\:\:\mathrm{637123}\:\mathrm{mod}\left(\mathrm{1000003}\right)\:\mathrm{what}\:\mathrm{i}\:\mathrm{have}\:\mathrm{note}\:\mathrm{a} \\ $$
