Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 70913 by TawaTawa last updated on 09/Oct/19

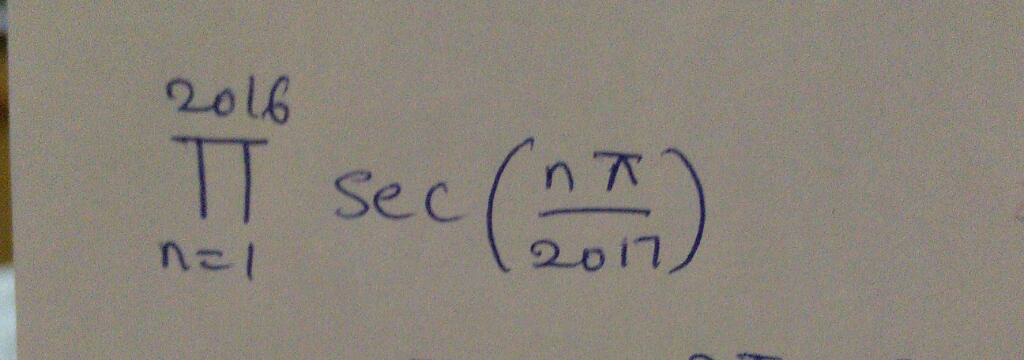
Commented by mathmax by abdo last updated on 10/Oct/19

we have ((z^(2017) −1)/(z−1)) =Π_(k=1) ^(2016) (z−e^((i2kπ)/(2017)) ) z=−1 ⇒1 =Π_(k=1) ^(2016) (−1−e^((i2kπ)/(2017)) ) =Π_(k=1) ^(2016) (1+e^((i2kπ)/(2017)) ) =Π_(k=1) ^(2016) (1+cos(((2kπ)/(2017)))+isin(((2kπ)/(2017)))) =Π_(k=1) ^(2016) (2cos^2 (((kπ)/(2017)))+2icos(((kπ)/(2017)))sin(((kπ)/(2017)))) =2^(2016) Π_(k=) ^(2016) cos(((kπ)/(2017)))Π_(k=1) ^(2016) e^((ikπ)/(2017)) =2^(2016) Π_(k=1) ^(2016) cos(((kπ)/(2017)))e^(((iπ)/(2017))Σ_(k=1) ^(2016) k) =2^(2016) Π_(k=1) ^(2016) cos(((kπ)/(2017))) e^(((iπ)/(2017))((2016.2017)/2)) =i^(2016) .2^(2016) Π_(k=1) ^(2016) cos(((kπ)/(2017))) ⇒Π_(k=1) ^(2016) cos(((kπ)/(2017)))=(1/2^(2016) ) ⇒ Π_(k=1) ^(2016) (1/(cos(((kπ)/(2017))))) =2^(2016)

$${we}\:{have}\:\frac{{z}^{\mathrm{2017}} −\mathrm{1}}{{z}−\mathrm{1}}\:=\prod_{{k}=\mathrm{1}} ^{\mathrm{2016}} \left({z}−{e}^{\frac{{i}\mathrm{2}{k}\pi}{\mathrm{2017}}} \right) \\ $$$${z}=−\mathrm{1}\:\Rightarrow\mathrm{1}\:=\prod_{{k}=\mathrm{1}} ^{\mathrm{2016}} \left(−\mathrm{1}−{e}^{\frac{{i}\mathrm{2}{k}\pi}{\mathrm{2017}}} \right)\:=\prod_{{k}=\mathrm{1}} ^{\mathrm{2016}} \left(\mathrm{1}+{e}^{\frac{{i}\mathrm{2}{k}\pi}{\mathrm{2017}}} \right) \\ $$$$=\prod_{{k}=\mathrm{1}} ^{\mathrm{2016}} \left(\mathrm{1}+{cos}\left(\frac{\mathrm{2}{k}\pi}{\mathrm{2017}}\right)+{isin}\left(\frac{\mathrm{2}{k}\pi}{\mathrm{2017}}\right)\right) \\ $$$$=\prod_{{k}=\mathrm{1}} ^{\mathrm{2016}} \left(\mathrm{2}{cos}^{\mathrm{2}} \left(\frac{{k}\pi}{\mathrm{2017}}\right)+\mathrm{2}{icos}\left(\frac{{k}\pi}{\mathrm{2017}}\right){sin}\left(\frac{{k}\pi}{\mathrm{2017}}\right)\right) \\ $$$$=\mathrm{2}^{\mathrm{2016}} \:\prod_{{k}=} ^{\mathrm{2016}} {cos}\left(\frac{{k}\pi}{\mathrm{2017}}\right)\prod_{{k}=\mathrm{1}} ^{\mathrm{2016}} {e}^{\frac{{ik}\pi}{\mathrm{2017}}} \\ $$$$=\mathrm{2}^{\mathrm{2016}} \:\prod_{{k}=\mathrm{1}} ^{\mathrm{2016}} \:{cos}\left(\frac{{k}\pi}{\mathrm{2017}}\right){e}^{\frac{{i}\pi}{\mathrm{2017}}\sum_{{k}=\mathrm{1}} ^{\mathrm{2016}} \:{k}} \\ $$$$=\mathrm{2}^{\mathrm{2016}} \:\prod_{{k}=\mathrm{1}} ^{\mathrm{2016}} \:{cos}\left(\frac{{k}\pi}{\mathrm{2017}}\right)\:{e}^{\frac{{i}\pi}{\mathrm{2017}}\frac{\mathrm{2016}.\mathrm{2017}}{\mathrm{2}}} \\ $$$$={i}^{\mathrm{2016}} \:.\mathrm{2}^{\mathrm{2016}} \:\prod_{{k}=\mathrm{1}} ^{\mathrm{2016}} \:{cos}\left(\frac{{k}\pi}{\mathrm{2017}}\right)\:\Rightarrow\prod_{{k}=\mathrm{1}} ^{\mathrm{2016}} \:{cos}\left(\frac{{k}\pi}{\mathrm{2017}}\right)=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2016}} }\:\Rightarrow \\ $$$$\prod_{{k}=\mathrm{1}} ^{\mathrm{2016}} \:\frac{\mathrm{1}}{{cos}\left(\frac{{k}\pi}{\mathrm{2017}}\right)}\:=\mathrm{2}^{\mathrm{2016}} \\ $$

Commented by mathmax by abdo last updated on 10/Oct/19

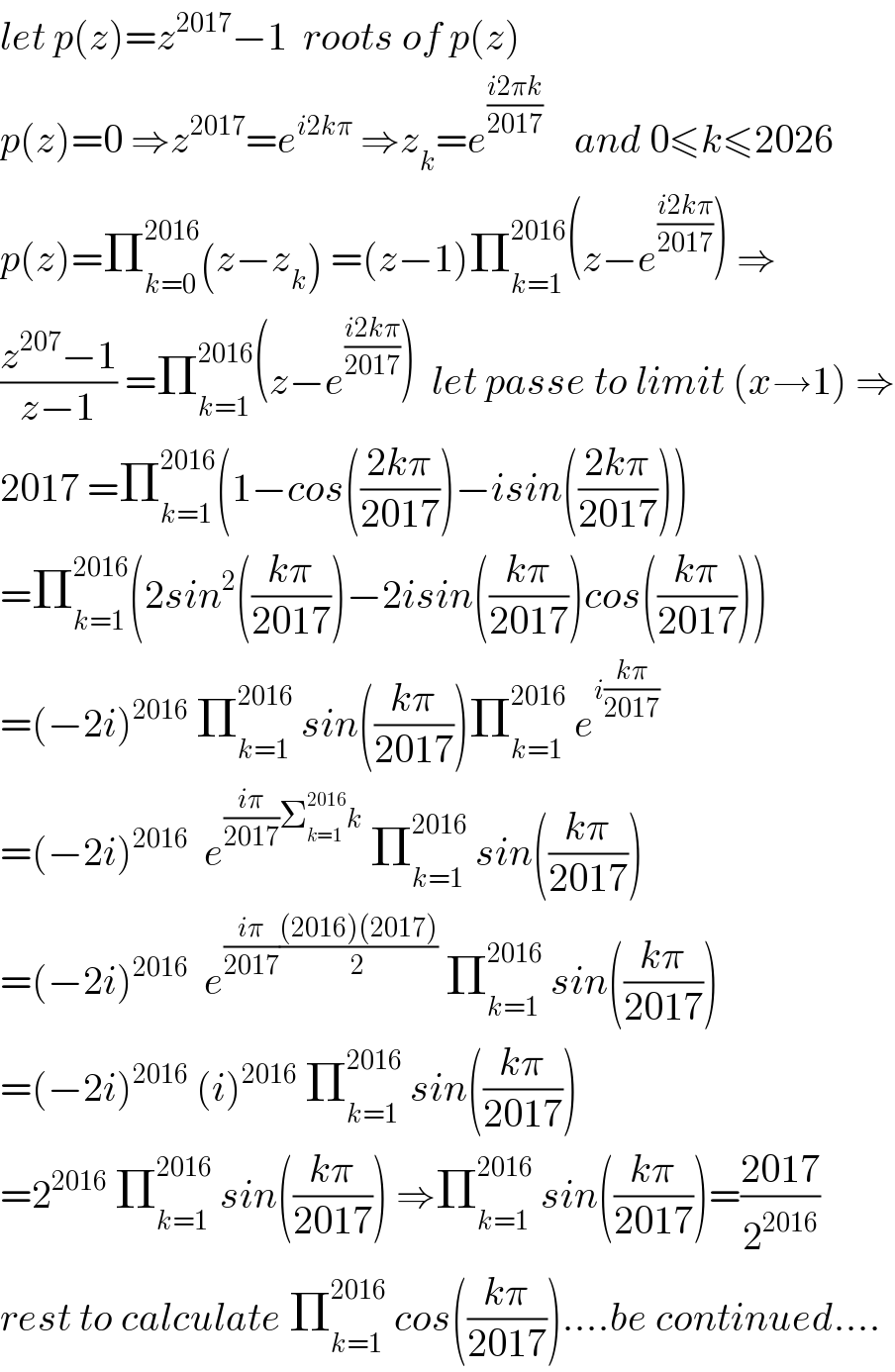
let p(z)=z^(2017) −1 roots of p(z) p(z)=0 ⇒z^(2017) =e^(i2kπ) ⇒z_k =e^((i2πk)/(2017)) and 0≤k≤2026 p(z)=Π_(k=0) ^(2016) (z−z_k ) =(z−1)Π_(k=1) ^(2016) (z−e^((i2kπ)/(2017)) ) ⇒ ((z^(207) −1)/(z−1)) =Π_(k=1) ^(2016) (z−e^((i2kπ)/(2017)) ) let passe to limit (x→1) ⇒ 2017 =Π_(k=1) ^(2016) (1−cos(((2kπ)/(2017)))−isin(((2kπ)/(2017)))) =Π_(k=1) ^(2016) (2sin^2 (((kπ)/(2017)))−2isin(((kπ)/(2017)))cos(((kπ)/(2017)))) =(−2i)^(2016) Π_(k=1) ^(2016) sin(((kπ)/(2017)))Π_(k=1) ^(2016) e^(i((kπ)/(2017))) =(−2i)^(2016) e^(((iπ)/(2017))Σ_(k=1) ^(2016) k) Π_(k=1) ^(2016) sin(((kπ)/(2017))) =(−2i)^(2016) e^(((iπ)/(2017))(((2016)(2017))/2)) Π_(k=1) ^(2016) sin(((kπ)/(2017))) =(−2i)^(2016) (i)^(2016) Π_(k=1) ^(2016) sin(((kπ)/(2017))) =2^(2016) Π_(k=1) ^(2016) sin(((kπ)/(2017))) ⇒Π_(k=1) ^(2016) sin(((kπ)/(2017)))=((2017)/2^(2016) ) rest to calculate Π_(k=1) ^(2016) cos(((kπ)/(2017)))....be continued....

$${let}\:{p}\left({z}\right)={z}^{\mathrm{2017}} −\mathrm{1}\:\:{roots}\:{of}\:{p}\left({z}\right) \\ $$$${p}\left({z}\right)=\mathrm{0}\:\Rightarrow{z}^{\mathrm{2017}} ={e}^{{i}\mathrm{2}{k}\pi} \:\Rightarrow{z}_{{k}} ={e}^{\frac{{i}\mathrm{2}\pi{k}}{\mathrm{2017}}} \:\:\:\:{and}\:\mathrm{0}\leqslant{k}\leqslant\mathrm{2026} \\ $$$${p}\left({z}\right)=\prod_{{k}=\mathrm{0}} ^{\mathrm{2016}} \left({z}−{z}_{{k}} \right)\:=\left({z}−\mathrm{1}\right)\prod_{{k}=\mathrm{1}} ^{\mathrm{2016}} \left({z}−{e}^{\frac{{i}\mathrm{2}{k}\pi}{\mathrm{2017}}} \right)\:\Rightarrow \\ $$$$\frac{{z}^{\mathrm{207}} −\mathrm{1}}{{z}−\mathrm{1}}\:=\prod_{{k}=\mathrm{1}} ^{\mathrm{2016}} \left({z}−{e}^{\frac{{i}\mathrm{2}{k}\pi}{\mathrm{2017}}} \right)\:\:{let}\:{passe}\:{to}\:{limit}\:\left({x}\rightarrow\mathrm{1}\right)\:\Rightarrow \\ $$$$\mathrm{2017}\:=\prod_{{k}=\mathrm{1}} ^{\mathrm{2016}} \left(\mathrm{1}−{cos}\left(\frac{\mathrm{2}{k}\pi}{\mathrm{2017}}\right)−{isin}\left(\frac{\mathrm{2}{k}\pi}{\mathrm{2017}}\right)\right) \\ $$$$=\prod_{{k}=\mathrm{1}} ^{\mathrm{2016}} \left(\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{{k}\pi}{\mathrm{2017}}\right)−\mathrm{2}{isin}\left(\frac{{k}\pi}{\mathrm{2017}}\right){cos}\left(\frac{{k}\pi}{\mathrm{2017}}\right)\right) \\ $$$$=\left(−\mathrm{2}{i}\right)^{\mathrm{2016}} \:\prod_{{k}=\mathrm{1}} ^{\mathrm{2016}} \:{sin}\left(\frac{{k}\pi}{\mathrm{2017}}\right)\prod_{{k}=\mathrm{1}} ^{\mathrm{2016}} \:{e}^{{i}\frac{{k}\pi}{\mathrm{2017}}} \\ $$$$=\left(−\mathrm{2}{i}\right)^{\mathrm{2016}} \:\:{e}^{\frac{{i}\pi}{\mathrm{2017}}\sum_{{k}=\mathrm{1}} ^{\mathrm{2016}} {k}} \:\prod_{{k}=\mathrm{1}} ^{\mathrm{2016}} \:{sin}\left(\frac{{k}\pi}{\mathrm{2017}}\right) \\ $$$$=\left(−\mathrm{2}{i}\right)^{\mathrm{2016}} \:\:{e}^{\frac{{i}\pi}{\mathrm{2017}}\frac{\left(\mathrm{2016}\right)\left(\mathrm{2017}\right)}{\mathrm{2}}} \:\prod_{{k}=\mathrm{1}} ^{\mathrm{2016}} \:{sin}\left(\frac{{k}\pi}{\mathrm{2017}}\right) \\ $$$$=\left(−\mathrm{2}{i}\right)^{\mathrm{2016}} \:\left({i}\right)^{\mathrm{2016}} \:\prod_{{k}=\mathrm{1}} ^{\mathrm{2016}} \:{sin}\left(\frac{{k}\pi}{\mathrm{2017}}\right) \\ $$$$=\mathrm{2}^{\mathrm{2016}} \:\prod_{{k}=\mathrm{1}} ^{\mathrm{2016}} \:{sin}\left(\frac{{k}\pi}{\mathrm{2017}}\right)\:\Rightarrow\prod_{{k}=\mathrm{1}} ^{\mathrm{2016}} \:{sin}\left(\frac{{k}\pi}{\mathrm{2017}}\right)=\frac{\mathrm{2017}}{\mathrm{2}^{\mathrm{2016}} } \\ $$$${rest}\:{to}\:{calculate}\:\prod_{{k}=\mathrm{1}} ^{\mathrm{2016}} \:{cos}\left(\frac{{k}\pi}{\mathrm{2017}}\right)....{be}\:{continued}.... \\ $$

Commented by TawaTawa last updated on 10/Oct/19

God bless you sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by mathmax by abdo last updated on 10/Oct/19

you are welcome.

$${you}\:{are}\:{welcome}. \\ $$

Answered by mind is power last updated on 10/Oct/19

Π_(n=1) ^(2016) ((e^(inx) +e^(−inx) )/2)=(1/2^(2016) ).Π_(n=1) ^(2016) (e^(2inx) +1).(1/(Π_(n=1) ^(2016) e^(inx) )) x=(π/(2017)) Z^(2017) −1=0⇒Z^(2017) =e^(2ikπ) Z=e^(i((2kπ)/(2017))) ,k∈{0,1,,2016} Z^(2017) −1=(z−1).Π_(k=1) ^(k=2016) (z−e^((2ikπ)/(2017)) ) ⇒Π_(k=1) ^(2016) (−1−e^((2kπ)/(2017)) )=(((−1)^(2017) −1)/(−2)) ⇒Π_(n=1) ^(2016) (−1)(1+e^(2inx) )=1 ⇒Π_(n=1) ^(2016) (1+e^(2inx) )=1 ⇒∐_(n=1) ^(2016) cos(nx)=(1/2^(2016) ).1.(1/e^(ixΣ_(n=1) ^(2016) n) ) Σ_1 ^(2016) n=1008.2017 e^(ixΣn) =e^(i(π/(2017)) .2017.1008) =e^(i1008π) =1 ⇒∐_(n=1) ^(2016) cos(((nπ)/(2017)))=(1/2^(2016) )⇒Π_(n=1) ^(2016) sec(((nπ)/(2017)))=2^(2016)

$$\underset{{n}=\mathrm{1}} {\overset{\mathrm{2016}} {\prod}}\frac{{e}^{{inx}} +{e}^{−{inx}} }{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2016}} }.\underset{{n}=\mathrm{1}} {\overset{\mathrm{2016}} {\prod}}\left({e}^{\mathrm{2}{inx}} +\mathrm{1}\right).\frac{\mathrm{1}}{\underset{{n}=\mathrm{1}} {\overset{\mathrm{2016}} {\prod}}{e}^{{inx}} }\:\:\:{x}=\frac{\pi}{\mathrm{2017}} \\ $$$${Z}^{\mathrm{2017}} −\mathrm{1}=\mathrm{0}\Rightarrow{Z}^{\mathrm{2017}} ={e}^{\mathrm{2}{ik}\pi} \\ $$$${Z}={e}^{{i}\frac{\mathrm{2}{k}\pi}{\mathrm{2017}}} ,{k}\in\left\{\mathrm{0},\mathrm{1},,\mathrm{2016}\right\} \\ $$$${Z}^{\mathrm{2017}} −\mathrm{1}=\left({z}−\mathrm{1}\right).\underset{{k}=\mathrm{1}} {\overset{{k}=\mathrm{2016}} {\prod}}\left({z}−{e}^{\frac{\mathrm{2}{ik}\pi}{\mathrm{2017}}} \right) \\ $$$$\Rightarrow\underset{{k}=\mathrm{1}} {\overset{\mathrm{2016}} {\prod}}\left(−\mathrm{1}−{e}^{\frac{\mathrm{2}{k}\pi}{\mathrm{2017}}} \right)=\frac{\left(−\mathrm{1}\right)^{\mathrm{2017}} −\mathrm{1}}{−\mathrm{2}} \\ $$$$\Rightarrow\underset{{n}=\mathrm{1}} {\overset{\mathrm{2016}} {\prod}}\left(−\mathrm{1}\right)\left(\mathrm{1}+{e}^{\mathrm{2}{inx}} \right)=\mathrm{1} \\ $$$$\Rightarrow\underset{{n}=\mathrm{1}} {\overset{\mathrm{2016}} {\prod}}\left(\mathrm{1}+{e}^{\mathrm{2}{inx}} \right)=\mathrm{1} \\ $$$$\Rightarrow\underset{{n}=\mathrm{1}} {\overset{\mathrm{2016}} {\coprod}}{cos}\left({nx}\right)=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2016}} }.\mathrm{1}.\frac{\mathrm{1}}{{e}^{{ix}\underset{{n}=\mathrm{1}} {\overset{\mathrm{2016}} {\sum}}{n}} } \\ $$$$\underset{\mathrm{1}} {\overset{\mathrm{2016}} {\sum}}{n}=\mathrm{1008}.\mathrm{2017} \\ $$$${e}^{{ix}\Sigma{n}} ={e}^{{i}\frac{\pi}{\mathrm{2017}}\:.\mathrm{2017}.\mathrm{1008}} ={e}^{{i}\mathrm{1008}\pi} =\mathrm{1} \\ $$$$\Rightarrow\underset{{n}=\mathrm{1}} {\overset{\mathrm{2016}} {\coprod}}{cos}\left(\frac{{n}\pi}{\mathrm{2017}}\right)=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2016}} }\Rightarrow\underset{{n}=\mathrm{1}} {\overset{\mathrm{2016}} {\prod}}{sec}\left(\frac{{n}\pi}{\mathrm{2017}}\right)=\mathrm{2}^{\mathrm{2016}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by TawaTawa last updated on 10/Oct/19

God bless you sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by mind is power last updated on 10/Oct/19

y′re welcom

$${y}'{re}\:{welcom} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com