Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 70452 by ajfour last updated on 04/Oct/19

Commented by ajfour last updated on 04/Oct/19

ABCD is a square. Find minimum side length s of equilateral △DEF in terms of quarter circle radii a and b. Also find range of (a/b) so that such an equilateral triangle be certainly possible.

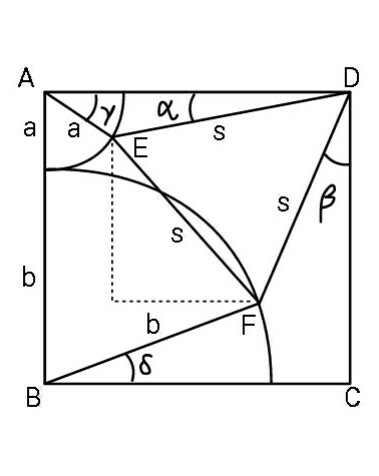
$${ABCD}\:{is}\:{a}\:{square}.\:{Find}\:{minimum} \\ $$$${side}\:{length}\:\boldsymbol{{s}}\:{of}\:{equilateral}\:\bigtriangleup{DEF} \\ $$$${in}\:{terms}\:{of}\:{quarter}\:{circle}\:{radii} \\ $$$${a}\:{and}\:{b}.\:{Also}\:{find}\:{range}\:{of}\: \\ $$$$\:\frac{{a}}{{b}}\:{so}\:{that}\:{such}\:{an}\:{equilateral} \\ $$$${triangle}\:{be}\:{certainly}\:{possible}. \\ $$

Commented by MJS last updated on 05/Oct/19

I tried with coordinate method A= ((0),(1) ) B= ((0),(0) ) C= ((1),(0) ) D= ((1),(1) ) E= (((acos α)),((1+asin α)) ) F= ((((1−a)cos β)),(((1−a)sin β)) ) ∣DE∣=∣EF∣=∣FD∣ easily leads to a=((1−(sin β +cos β))/(1−(cos α +sin β +cos β))) then I put α=2arctan t β=2arctan u which leads to t^4 −((8u(u−1)^2 (3u−1))/((3u^2 −1)(5u^2 −4u+1)))t^3 −((2(7u^4 −4u^3 −2u^2 +4u−1))/((3u^2 −1)(5u^2 −4u+1)))t^2 −((8u(u−1)^2 (u+1))/((3u^2 −1)(5u^2 −4u+1)))t−(((u^2 +1)(u^2 −4u+1))/((3u^2 −1)(5u^2 −4u+1)))=0 and we can solve this! t_1 =(((3+2(√3))u^2 −2(1+(√3))u+1)/(3u^2 −1)) t_2 =(((3−3(√2))u^2 −2(1−(√3))u+1)/(3u^2 −1)) t_(3, 4) =−((u^2 +2u−1)/(5u^2 −4u+1))±((2u(u−1))/(5u^2 −4u+1))i I′m running out of time, please try to continue

$$\mathrm{I}\:\mathrm{tried}\:\mathrm{with}\:\mathrm{coordinate}\:\mathrm{method} \\ $$$${A}=\begin{pmatrix}{\mathrm{0}}\\{\mathrm{1}}\end{pmatrix}\:\:{B}=\begin{pmatrix}{\mathrm{0}}\\{\mathrm{0}}\end{pmatrix}\:\:{C}=\begin{pmatrix}{\mathrm{1}}\\{\mathrm{0}}\end{pmatrix}\:\:{D}=\begin{pmatrix}{\mathrm{1}}\\{\mathrm{1}}\end{pmatrix} \\ $$$${E}=\begin{pmatrix}{{a}\mathrm{cos}\:\alpha}\\{\mathrm{1}+{a}\mathrm{sin}\:\alpha}\end{pmatrix}\:\:{F}=\begin{pmatrix}{\left(\mathrm{1}−{a}\right)\mathrm{cos}\:\beta}\\{\left(\mathrm{1}−{a}\right)\mathrm{sin}\:\beta}\end{pmatrix} \\ $$$$\mid{DE}\mid=\mid{EF}\mid=\mid{FD}\mid \\ $$$$\mathrm{easily}\:\mathrm{leads}\:\mathrm{to} \\ $$$${a}=\frac{\mathrm{1}−\left(\mathrm{sin}\:\beta\:+\mathrm{cos}\:\beta\right)}{\mathrm{1}−\left(\mathrm{cos}\:\alpha\:+\mathrm{sin}\:\beta\:+\mathrm{cos}\:\beta\right)} \\ $$$$\mathrm{then}\:\mathrm{I}\:\mathrm{put} \\ $$$$\alpha=\mathrm{2arctan}\:{t} \\ $$$$\beta=\mathrm{2arctan}\:{u} \\ $$$$\mathrm{which}\:\mathrm{leads}\:\mathrm{to} \\ $$$${t}^{\mathrm{4}} −\frac{\mathrm{8}{u}\left({u}−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{3}{u}−\mathrm{1}\right)}{\left(\mathrm{3}{u}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{5}{u}^{\mathrm{2}} −\mathrm{4}{u}+\mathrm{1}\right)}{t}^{\mathrm{3}} −\frac{\mathrm{2}\left(\mathrm{7}{u}^{\mathrm{4}} −\mathrm{4}{u}^{\mathrm{3}} −\mathrm{2}{u}^{\mathrm{2}} +\mathrm{4}{u}−\mathrm{1}\right)}{\left(\mathrm{3}{u}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{5}{u}^{\mathrm{2}} −\mathrm{4}{u}+\mathrm{1}\right)}{t}^{\mathrm{2}} −\frac{\mathrm{8}{u}\left({u}−\mathrm{1}\right)^{\mathrm{2}} \left({u}+\mathrm{1}\right)}{\left(\mathrm{3}{u}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{5}{u}^{\mathrm{2}} −\mathrm{4}{u}+\mathrm{1}\right)}{t}−\frac{\left({u}^{\mathrm{2}} +\mathrm{1}\right)\left({u}^{\mathrm{2}} −\mathrm{4}{u}+\mathrm{1}\right)}{\left(\mathrm{3}{u}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{5}{u}^{\mathrm{2}} −\mathrm{4}{u}+\mathrm{1}\right)}=\mathrm{0} \\ $$$$\mathrm{and}\:\mathrm{we}\:\mathrm{can}\:\mathrm{solve}\:\mathrm{this}! \\ $$$${t}_{\mathrm{1}} =\frac{\left(\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}\right){u}^{\mathrm{2}} −\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{3}}\right){u}+\mathrm{1}}{\mathrm{3}{u}^{\mathrm{2}} −\mathrm{1}} \\ $$$${t}_{\mathrm{2}} =\frac{\left(\mathrm{3}−\mathrm{3}\sqrt{\mathrm{2}}\right){u}^{\mathrm{2}} −\mathrm{2}\left(\mathrm{1}−\sqrt{\mathrm{3}}\right){u}+\mathrm{1}}{\mathrm{3}{u}^{\mathrm{2}} −\mathrm{1}} \\ $$$${t}_{\mathrm{3},\:\mathrm{4}} =−\frac{{u}^{\mathrm{2}} +\mathrm{2}{u}−\mathrm{1}}{\mathrm{5}{u}^{\mathrm{2}} −\mathrm{4}{u}+\mathrm{1}}\pm\frac{\mathrm{2}{u}\left({u}−\mathrm{1}\right)}{\mathrm{5}{u}^{\mathrm{2}} −\mathrm{4}{u}+\mathrm{1}}\mathrm{i} \\ $$$$\mathrm{I}'\mathrm{m}\:\mathrm{running}\:\mathrm{out}\:\mathrm{of}\:\mathrm{time},\:\mathrm{please}\:\mathrm{try}\:\mathrm{to}\:\mathrm{continue} \\ $$

Commented by mr W last updated on 05/Oct/19

Commented by mr W last updated on 05/Oct/19

a geometrical consideration: the green circle can intersect with the smaller quarter−circle at − no point ⇒ no solution − one point ⇒ one solution − two points ⇒ two solutions

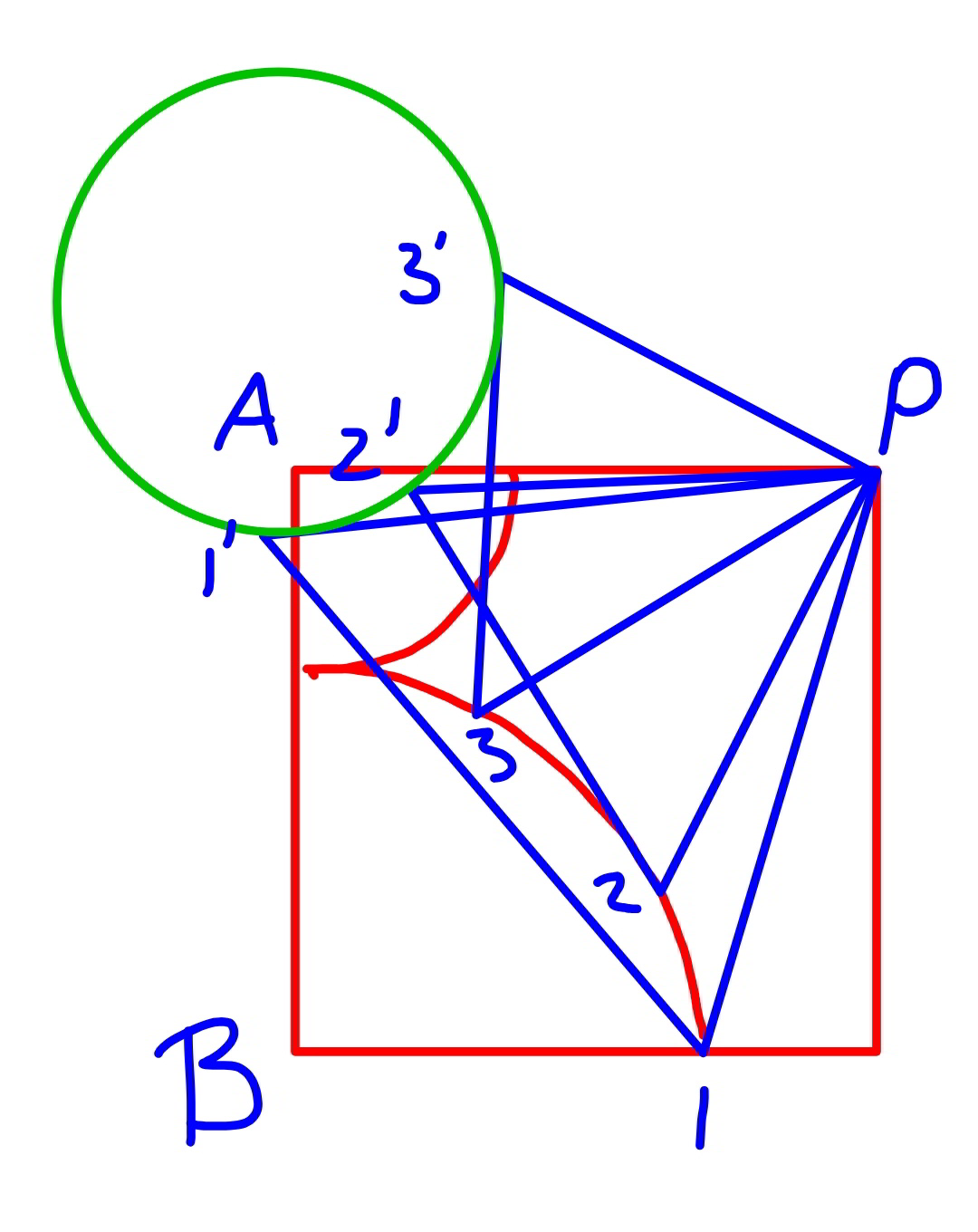
$${a}\:{geometrical}\:{consideration}: \\ $$$${the}\:{green}\:{circle}\:{can}\:{intersect}\:{with}\:{the} \\ $$$${smaller}\:{quarter}−{circle}\:{at} \\ $$$$−\:{no}\:{point}\:\Rightarrow\:{no}\:{solution} \\ $$$$−\:{one}\:{point}\:\Rightarrow\:{one}\:{solution} \\ $$$$−\:{two}\:{points}\:\Rightarrow\:{two}\:{solutions} \\ $$

Answered by mr W last updated on 10/Oct/19

Answered by ajfour last updated on 04/Oct/19

Terms of Service

Privacy Policy

Contact: info@tinkutara.com