
Question Number 69829 by TawaTawa last updated on 28/Sep/19

Commented by TawaTawa last updated on 28/Sep/19
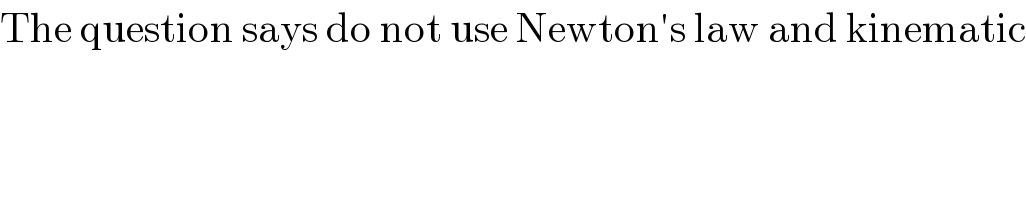
$$\mathrm{The}\:\mathrm{question}\:\mathrm{says}\:\mathrm{do}\:\mathrm{not}\:\mathrm{use}\:\mathrm{Newton}'\mathrm{s}\:\mathrm{law}\:\mathrm{and}\:\mathrm{kinematic} \\ $$
Commented by TawaTawa last updated on 28/Sep/19
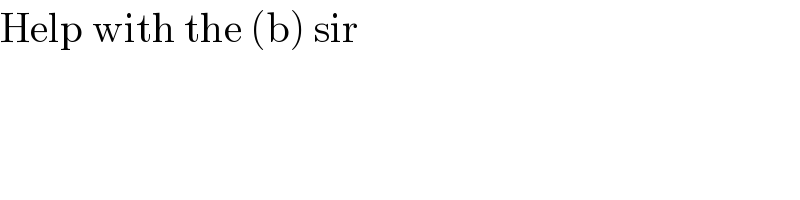
$$\mathrm{Help}\:\mathrm{with}\:\mathrm{the}\:\left(\mathrm{b}\right)\:\mathrm{sir} \\ $$
Answered by mr W last updated on 28/Sep/19

$$\left({b}\right) \\ $$$${energy}\:{at}\:{the}\:{beginning}: \\ $$$${E}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}{mv}^{\mathrm{2}} \\ $$$${energy}\:{at}\:{the}\:{end}: \\ $$$${E}_{\mathrm{2}} ={mgh} \\ $$$${work}\:{done}\:{by}\:{the}\:{gravity}\:{force}: \\ $$$$−{mgh} \\ $$$${friction}\:{force}: \\ $$$${f}=\mu{N}=\mu{mg}\:\mathrm{cos}\:\theta \\ $$$${work}\:{done}\:{by}\:{the}\:{friction}\:{force}: \\ $$$$−{fs}=−{f}\:\frac{{h}}{\mathrm{sin}\:\theta}=−\frac{\mu{mgh}}{\mathrm{tan}\:\theta} \\ $$$${work}={energy}\:{change} \\ $$$$−{mgh}−\frac{\mu{mgh}}{\mathrm{tan}\:\theta}={mgh}−\frac{\mathrm{1}}{\mathrm{2}}{mv}^{\mathrm{2}} \\ $$$$\Rightarrow\mu=\left(\mathrm{2}−\frac{{v}^{\mathrm{2}} }{\mathrm{2}{gh}}\right)\mathrm{tan}\:\theta=\left(\mathrm{2}−\frac{\mathrm{12}^{\mathrm{2}} }{\mathrm{2}×\mathrm{10}×\mathrm{5}}\right)×\mathrm{tan}\:\mathrm{45}°=\mathrm{0}.\mathrm{56} \\ $$
Commented by TawaTawa last updated on 28/Sep/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by mr W last updated on 28/Sep/19
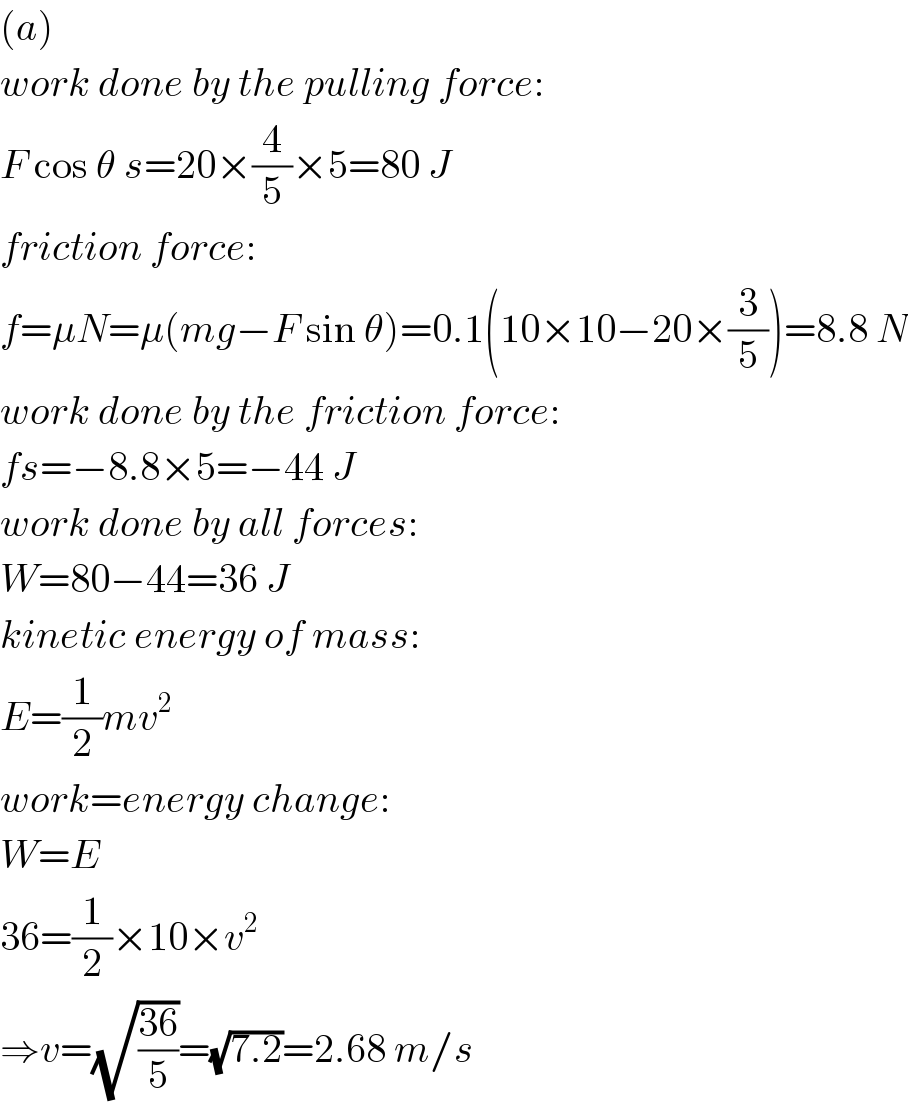
$$\left({a}\right) \\ $$$${work}\:{done}\:{by}\:{the}\:{pulling}\:{force}: \\ $$$${F}\:\mathrm{cos}\:\theta\:{s}=\mathrm{20}×\frac{\mathrm{4}}{\mathrm{5}}×\mathrm{5}=\mathrm{80}\:{J} \\ $$$${friction}\:{force}: \\ $$$${f}=\mu{N}=\mu\left({mg}−{F}\:\mathrm{sin}\:\theta\right)=\mathrm{0}.\mathrm{1}\left(\mathrm{10}×\mathrm{10}−\mathrm{20}×\frac{\mathrm{3}}{\mathrm{5}}\right)=\mathrm{8}.\mathrm{8}\:{N} \\ $$$${work}\:{done}\:{by}\:{the}\:{friction}\:{force}: \\ $$$${fs}=−\mathrm{8}.\mathrm{8}×\mathrm{5}=−\mathrm{44}\:{J} \\ $$$${work}\:{done}\:{by}\:{all}\:{forces}: \\ $$$${W}=\mathrm{80}−\mathrm{44}=\mathrm{36}\:{J} \\ $$$${kinetic}\:{energy}\:{of}\:{mass}: \\ $$$${E}=\frac{\mathrm{1}}{\mathrm{2}}{mv}^{\mathrm{2}} \\ $$$${work}={energy}\:{change}: \\ $$$${W}={E} \\ $$$$\mathrm{36}=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{10}×{v}^{\mathrm{2}} \\ $$$$\Rightarrow{v}=\sqrt{\frac{\mathrm{36}}{\mathrm{5}}}=\sqrt{\mathrm{7}.\mathrm{2}}=\mathrm{2}.\mathrm{68}\:{m}/{s} \\ $$
Commented by TawaTawa last updated on 28/Sep/19
$$\mathrm{Wow},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{time} \\ $$
