
Question Number 69665 by ozodbek last updated on 26/Sep/19
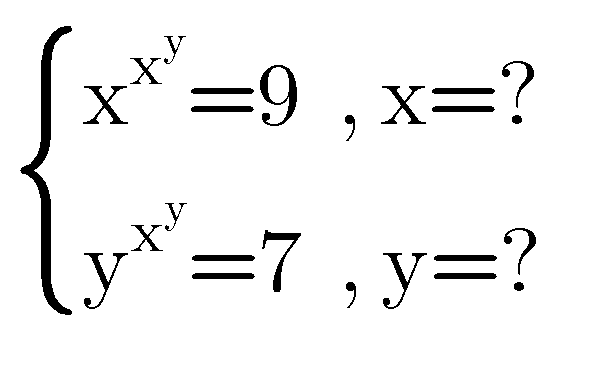
Commented by ozodbek last updated on 26/Sep/19

$$\mathrm{solve} \\ $$
Answered by mr W last updated on 26/Sep/19
![x^y ln x=ln 9 x^y =((ln 9)/(ln x)) yln x=ln (((ln 9)/(ln x)))=ln (ln 9)−ln (ln x) ⇒y=((ln (ln 9)−ln (ln x))/(ln x)) x^y ln y=ln 7 ((ln 9)/(ln x))ln y=ln 7 ln y=((ln 7 ln x)/(ln 9)) ln ((ln (ln 9)−ln (ln x))/(ln x))=((ln 7 ln x)/(ln 9)) ln [ln (ln 9)−ln (ln x)]−ln (ln x)=(((ln 7)/(ln 9)))ln x with t=ln x ln [ln (ln 9)−ln t]−ln t=(((ln 7)/(ln 9)))t ⇒t=ln x=0.664263 ⇒x=1.943058 ⇒ln y=0.588285 ⇒y=1.800899](Q69711.png)
$${x}^{{y}} \mathrm{ln}\:{x}=\mathrm{ln}\:\mathrm{9} \\ $$$${x}^{{y}} =\frac{\mathrm{ln}\:\mathrm{9}}{\mathrm{ln}\:{x}} \\ $$$${y}\mathrm{ln}\:{x}=\mathrm{ln}\:\left(\frac{\mathrm{ln}\:\mathrm{9}}{\mathrm{ln}\:{x}}\right)=\mathrm{ln}\:\left(\mathrm{ln}\:\mathrm{9}\right)−\mathrm{ln}\:\left(\mathrm{ln}\:{x}\right) \\ $$$$\Rightarrow{y}=\frac{\mathrm{ln}\:\left(\mathrm{ln}\:\mathrm{9}\right)−\mathrm{ln}\:\left(\mathrm{ln}\:{x}\right)}{\mathrm{ln}\:{x}} \\ $$$${x}^{{y}} \mathrm{ln}\:{y}=\mathrm{ln}\:\mathrm{7} \\ $$$$\frac{\mathrm{ln}\:\mathrm{9}}{\mathrm{ln}\:{x}}\mathrm{ln}\:{y}=\mathrm{ln}\:\mathrm{7} \\ $$$$\mathrm{ln}\:{y}=\frac{\mathrm{ln}\:\mathrm{7}\:\mathrm{ln}\:{x}}{\mathrm{ln}\:\mathrm{9}} \\ $$$$\mathrm{ln}\:\frac{\mathrm{ln}\:\left(\mathrm{ln}\:\mathrm{9}\right)−\mathrm{ln}\:\left(\mathrm{ln}\:{x}\right)}{\mathrm{ln}\:{x}}=\frac{\mathrm{ln}\:\mathrm{7}\:\mathrm{ln}\:{x}}{\mathrm{ln}\:\mathrm{9}} \\ $$$$\mathrm{ln}\:\left[\mathrm{ln}\:\left(\mathrm{ln}\:\mathrm{9}\right)−\mathrm{ln}\:\left(\mathrm{ln}\:{x}\right)\right]−\mathrm{ln}\:\left(\mathrm{ln}\:{x}\right)=\left(\frac{\mathrm{ln}\:\mathrm{7}}{\mathrm{ln}\:\mathrm{9}}\right)\mathrm{ln}\:{x} \\ $$$${with}\:{t}=\mathrm{ln}\:{x} \\ $$$$\mathrm{ln}\:\left[\mathrm{ln}\:\left(\mathrm{ln}\:\mathrm{9}\right)−\mathrm{ln}\:{t}\right]−\mathrm{ln}\:{t}=\left(\frac{\mathrm{ln}\:\mathrm{7}}{\mathrm{ln}\:\mathrm{9}}\right){t} \\ $$$$\Rightarrow{t}=\mathrm{ln}\:{x}=\mathrm{0}.\mathrm{664263} \\ $$$$\Rightarrow{x}=\mathrm{1}.\mathrm{943058} \\ $$$$\Rightarrow\mathrm{ln}\:{y}=\mathrm{0}.\mathrm{588285} \\ $$$$\Rightarrow{y}=\mathrm{1}.\mathrm{800899} \\ $$
Commented by ozodbek last updated on 27/Sep/19

$$\mathrm{thank}\:\mathrm{you} \\ $$
Commented by otchereabdullai@gmail.com last updated on 29/Sep/19

$$\mathrm{the}\:\mathrm{great}\:\mathrm{prof}\:\mathrm{W}\:\mathrm{you}\:\mathrm{are}\:\mathrm{truely}\:\mathrm{exceptional} \\ $$
Commented by mr W last updated on 29/Sep/19
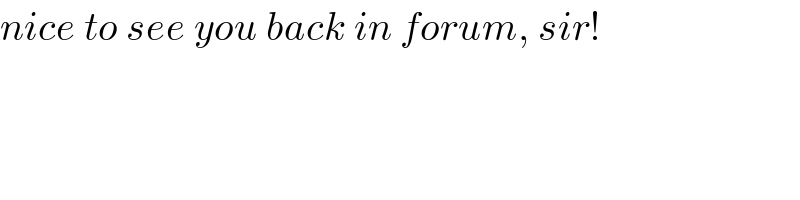
$${nice}\:{to}\:{see}\:{you}\:{back}\:{in}\:{forum},\:{sir}! \\ $$
