
Question Number 69500 by TawaTawa last updated on 24/Sep/19
Answered by MJS last updated on 24/Sep/19
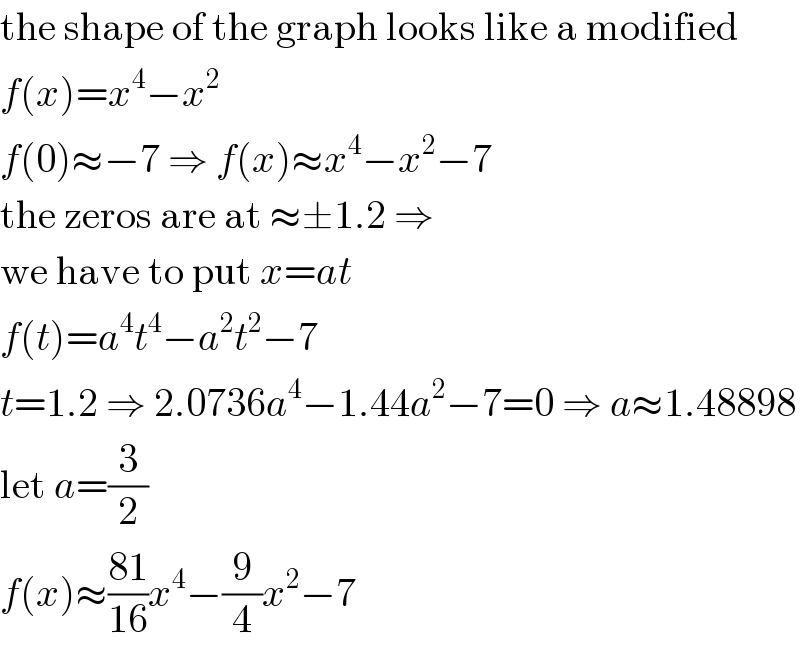
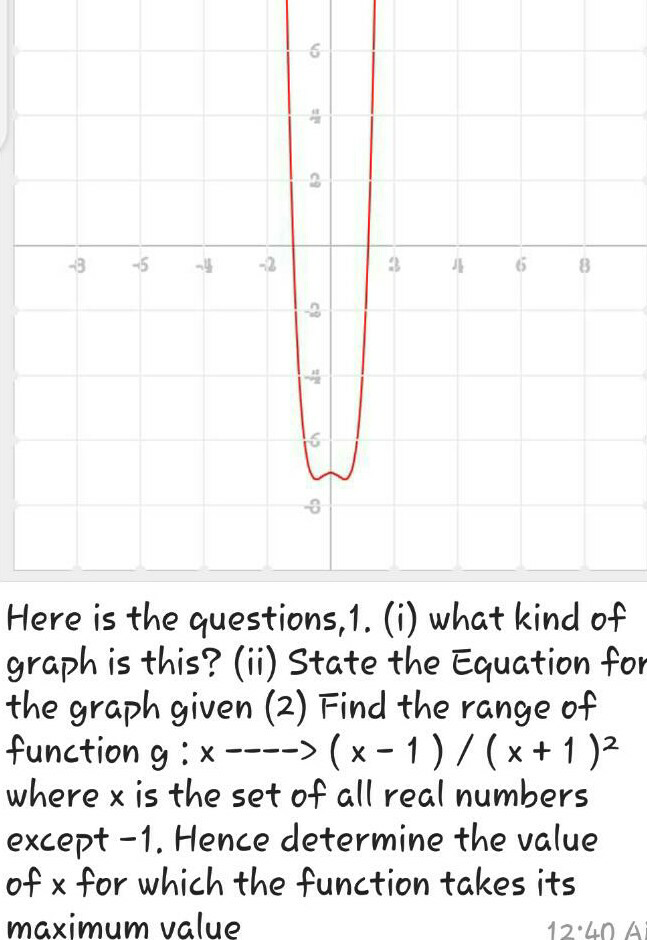
$$\mathrm{the}\:\mathrm{shape}\:\mathrm{of}\:\mathrm{the}\:\mathrm{graph}\:\mathrm{looks}\:\mathrm{like}\:\mathrm{a}\:\mathrm{modified} \\ $$$${f}\left({x}\right)={x}^{\mathrm{4}} −{x}^{\mathrm{2}} \\ $$$${f}\left(\mathrm{0}\right)\approx−\mathrm{7}\:\Rightarrow\:{f}\left({x}\right)\approx{x}^{\mathrm{4}} −{x}^{\mathrm{2}} −\mathrm{7} \\ $$$$\mathrm{the}\:\mathrm{zeros}\:\mathrm{are}\:\mathrm{at}\:\approx\pm\mathrm{1}.\mathrm{2}\:\Rightarrow \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{to}\:\mathrm{put}\:{x}={at} \\ $$$${f}\left({t}\right)={a}^{\mathrm{4}} {t}^{\mathrm{4}} −{a}^{\mathrm{2}} {t}^{\mathrm{2}} −\mathrm{7} \\ $$$${t}=\mathrm{1}.\mathrm{2}\:\Rightarrow\:\mathrm{2}.\mathrm{0736}{a}^{\mathrm{4}} −\mathrm{1}.\mathrm{44}{a}^{\mathrm{2}} −\mathrm{7}=\mathrm{0}\:\Rightarrow\:{a}\approx\mathrm{1}.\mathrm{48898} \\ $$$$\mathrm{let}\:{a}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$${f}\left({x}\right)\approx\frac{\mathrm{81}}{\mathrm{16}}{x}^{\mathrm{4}} −\frac{\mathrm{9}}{\mathrm{4}}{x}^{\mathrm{2}} −\mathrm{7} \\ $$
Commented by TawaTawa last updated on 24/Sep/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by MJS last updated on 24/Sep/19
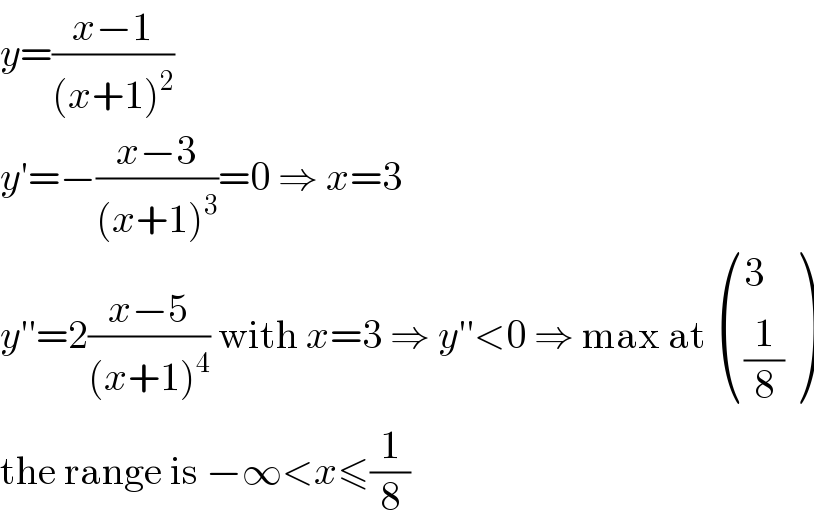
$${y}=\frac{{x}−\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${y}'=−\frac{{x}−\mathrm{3}}{\left({x}+\mathrm{1}\right)^{\mathrm{3}} }=\mathrm{0}\:\Rightarrow\:{x}=\mathrm{3} \\ $$$${y}''=\mathrm{2}\frac{{x}−\mathrm{5}}{\left({x}+\mathrm{1}\right)^{\mathrm{4}} }\:\mathrm{with}\:{x}=\mathrm{3}\:\Rightarrow\:{y}''<\mathrm{0}\:\Rightarrow\:\mathrm{max}\:\mathrm{at}\:\begin{pmatrix}{\mathrm{3}}\\{\frac{\mathrm{1}}{\mathrm{8}}}\end{pmatrix} \\ $$$$\mathrm{the}\:\mathrm{range}\:\mathrm{is}\:−\infty<{x}\leqslant\frac{\mathrm{1}}{\mathrm{8}} \\ $$
Commented by TawaTawa last updated on 24/Sep/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
