
Question Number 69412 by ahmadshah last updated on 23/Sep/19
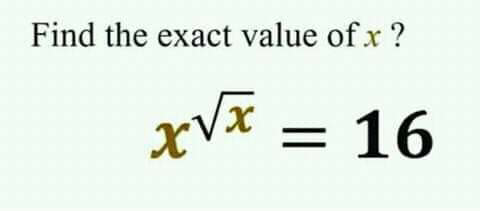
Commented by Rasheed.Sindhi last updated on 23/Sep/19

$${x}=\mathrm{4} \\ $$
Answered by mr W last updated on 23/Sep/19
![generally solve x^(√x) =a>0 x=a^(1/(√x)) ((√x))^2 =a^(1/(√x)) (√x)=a^(1/(2(√x))) (√x)=e^((ln a)/(2(√x))) ((ln a)/2)=((ln a)/(2(√x)))e^((ln a)/(2(√x))) ⇒((ln a)/(2(√x)))=W(((ln a)/2)) ⇒(√x)=((ln a)/(2W(((ln a)/2)))) ⇒x=[((ln a)/(2W(((ln a)/2))))]^2 with a=16: ln a=4 ln 2 x=[((2ln 2)/(W(2 ln 2)))]^2 =(((2 ln 2)/(0.69317418)))^2 =4 with a=5: x=[((ln 5)/(2W(((ln 5)/2))))]^2 =(((ln 5)/(2×0.492004741)))^2 ≈2.675161](Q69453.png)
$${generally}\:{solve}\:{x}^{\sqrt{{x}}} ={a}>\mathrm{0} \\ $$$${x}={a}^{\frac{\mathrm{1}}{\sqrt{{x}}}} \\ $$$$\left(\sqrt{{x}}\right)^{\mathrm{2}} ={a}^{\frac{\mathrm{1}}{\sqrt{{x}}}} \\ $$$$\sqrt{{x}}={a}^{\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}} \\ $$$$\sqrt{{x}}={e}^{\frac{\mathrm{ln}\:{a}}{\mathrm{2}\sqrt{{x}}}} \\ $$$$\frac{\mathrm{ln}\:{a}}{\mathrm{2}}=\frac{\mathrm{ln}\:{a}}{\mathrm{2}\sqrt{{x}}}{e}^{\frac{\mathrm{ln}\:{a}}{\mathrm{2}\sqrt{{x}}}} \\ $$$$\Rightarrow\frac{\mathrm{ln}\:{a}}{\mathrm{2}\sqrt{{x}}}={W}\left(\frac{\mathrm{ln}\:{a}}{\mathrm{2}}\right) \\ $$$$\Rightarrow\sqrt{{x}}=\frac{\mathrm{ln}\:{a}}{\mathrm{2}{W}\left(\frac{\mathrm{ln}\:{a}}{\mathrm{2}}\right)} \\ $$$$\Rightarrow{x}=\left[\frac{\mathrm{ln}\:{a}}{\mathrm{2}{W}\left(\frac{\mathrm{ln}\:{a}}{\mathrm{2}}\right)}\right]^{\mathrm{2}} \\ $$$$ \\ $$$${with}\:{a}=\mathrm{16}: \\ $$$$\mathrm{ln}\:{a}=\mathrm{4}\:\mathrm{ln}\:\mathrm{2} \\ $$$${x}=\left[\frac{\mathrm{2ln}\:\mathrm{2}}{{W}\left(\mathrm{2}\:\mathrm{ln}\:\mathrm{2}\right)}\right]^{\mathrm{2}} =\left(\frac{\mathrm{2}\:\mathrm{ln}\:\mathrm{2}}{\mathrm{0}.\mathrm{69317418}}\right)^{\mathrm{2}} =\mathrm{4} \\ $$$$ \\ $$$${with}\:{a}=\mathrm{5}: \\ $$$${x}=\left[\frac{\mathrm{ln}\:\mathrm{5}}{\mathrm{2}{W}\left(\frac{\mathrm{ln}\:\mathrm{5}}{\mathrm{2}}\right)}\right]^{\mathrm{2}} =\left(\frac{\mathrm{ln}\:\mathrm{5}}{\mathrm{2}×\mathrm{0}.\mathrm{492004741}}\right)^{\mathrm{2}} \approx\mathrm{2}.\mathrm{675161} \\ $$
