Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 69111 by Fawole last updated on 20/Sep/19

Commented by Rasheed.Sindhi last updated on 20/Sep/19

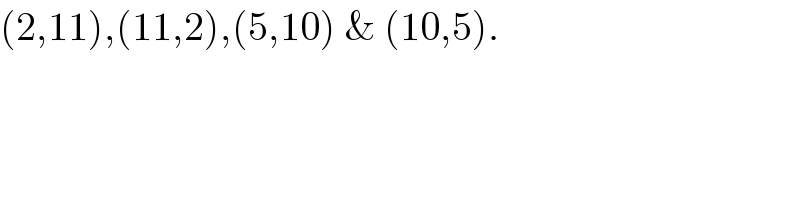
(2,11),(11,2),(5,10) & (10,5).

$$\left(\mathrm{2},\mathrm{11}\right),\left(\mathrm{11},\mathrm{2}\right),\left(\mathrm{5},\mathrm{10}\right)\:\&\:\left(\mathrm{10},\mathrm{5}\right). \\ $$

Commented by Fawole last updated on 20/Sep/19

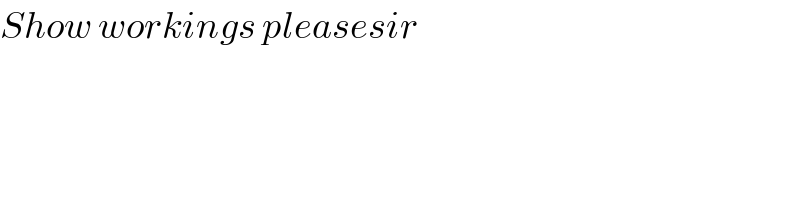
Show workings pleasesir

$${Show}\:{workings}\:{pleasesir} \\ $$

Answered by Rasheed.Sindhi last updated on 21/Sep/19

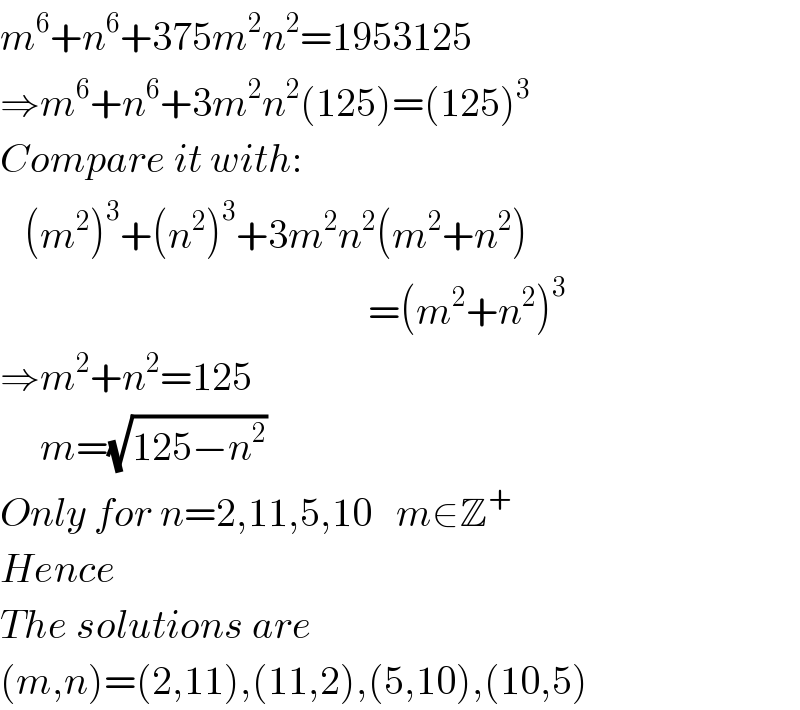
m^6 +n^6 +375m^2 n^2 =1953125 ⇒m^6 +n^6 +3m^2 n^2 (125)=(125)^3 Compare it with: (m^2 )^3 +(n^2 )^3 +3m^2 n^2 (m^2 +n^2 ) =(m^2 +n^2 )^3 ⇒m^2 +n^2 =125 m=(√(125−n^2 )) Only for n=2,11,5,10 m∈Z^+ Hence The solutions are (m,n)=(2,11),(11,2),(5,10),(10,5)

$${m}^{\mathrm{6}} +{n}^{\mathrm{6}} +\mathrm{375}{m}^{\mathrm{2}} {n}^{\mathrm{2}} =\mathrm{1953125} \\ $$$$\Rightarrow{m}^{\mathrm{6}} +{n}^{\mathrm{6}} +\mathrm{3}{m}^{\mathrm{2}} {n}^{\mathrm{2}} \left(\mathrm{125}\right)=\left(\mathrm{125}\right)^{\mathrm{3}} \\ $$$${Compare}\:{it}\:{with}: \\ $$$$\:\:\:\left({m}^{\mathrm{2}} \right)^{\mathrm{3}} +\left({n}^{\mathrm{2}} \right)^{\mathrm{3}} +\mathrm{3}{m}^{\mathrm{2}} {n}^{\mathrm{2}} \left({m}^{\mathrm{2}} +{n}^{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left({m}^{\mathrm{2}} +{n}^{\mathrm{2}} \right)^{\mathrm{3}} \\ $$$$\Rightarrow{m}^{\mathrm{2}} +{n}^{\mathrm{2}} =\mathrm{125} \\ $$$$\:\:\:\:\:{m}=\sqrt{\mathrm{125}−{n}^{\mathrm{2}} } \\ $$$${Only}\:{for}\:{n}=\mathrm{2},\mathrm{11},\mathrm{5},\mathrm{10}\:\:\:{m}\in\mathbb{Z}^{+} \\ $$$${Hence} \\ $$$${The}\:{solutions}\:{are} \\ $$$$\left({m},{n}\right)=\left(\mathrm{2},\mathrm{11}\right),\left(\mathrm{11},\mathrm{2}\right),\left(\mathrm{5},\mathrm{10}\right),\left(\mathrm{10},\mathrm{5}\right) \\ $$

Commented by mr W last updated on 21/Sep/19

nice solution!

$${nice}\:{solution}! \\ $$

Commented by Rasheed.Sindhi last updated on 21/Sep/19

Thαnks Sir!

$$\mathcal{T}{h}\alpha{nks}\:{Sir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com