
Question Number 68825 by peter frank last updated on 15/Sep/19

Answered by mind is power last updated on 16/Sep/19
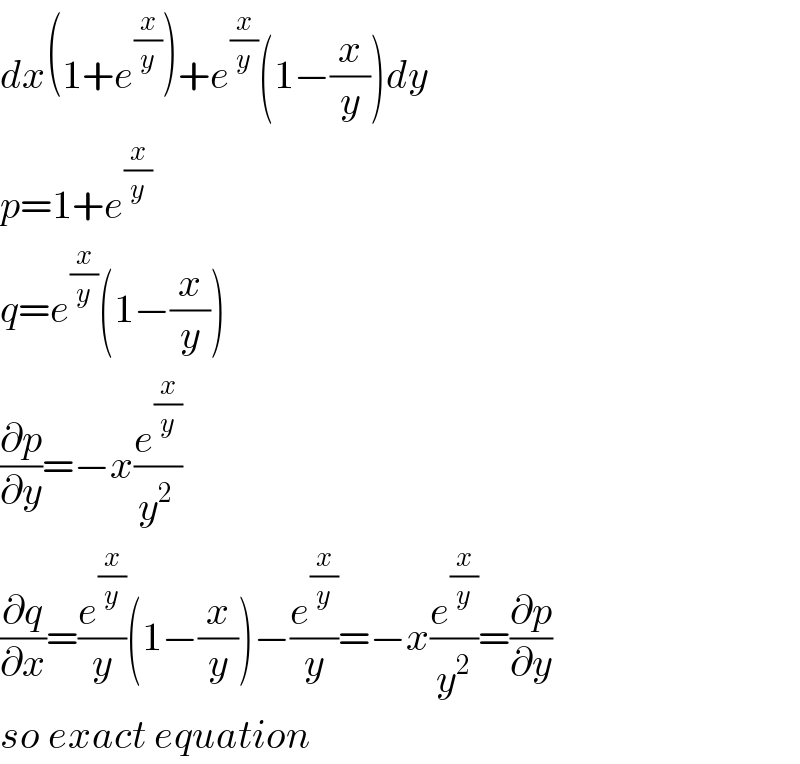
$${dx}\left(\mathrm{1}+{e}^{\frac{{x}}{{y}}} \right)+{e}^{\frac{{x}}{{y}}} \left(\mathrm{1}−\frac{{x}}{{y}}\right){dy} \\ $$$${p}=\mathrm{1}+{e}^{\frac{{x}}{{y}}} \\ $$$${q}={e}^{\frac{{x}}{{y}}} \left(\mathrm{1}−\frac{{x}}{{y}}\right) \\ $$$$\frac{\partial{p}}{\partial{y}}=−{x}\frac{{e}^{\frac{{x}}{{y}}} }{{y}^{\mathrm{2}\:} } \\ $$$$\frac{\partial{q}}{\partial{x}}=\frac{{e}^{\frac{{x}}{{y}}} }{{y}}\left(\mathrm{1}−\frac{{x}}{{y}}\right)−\frac{{e}^{\frac{{x}}{{y}}} }{{y}}=−{x}\frac{{e}^{\frac{{x}}{{y}}} }{{y}^{\mathrm{2}} }=\frac{\partial{p}}{\partial{y}} \\ $$$${so}\:{exact}\:{equation} \\ $$
Commented by peter frank last updated on 22/Sep/19

$${thank}\:{you} \\ $$
