
Question Number 68775 by rajesh4661kumar@gmail.com last updated on 15/Sep/19

Answered by $@ty@m123 last updated on 15/Sep/19
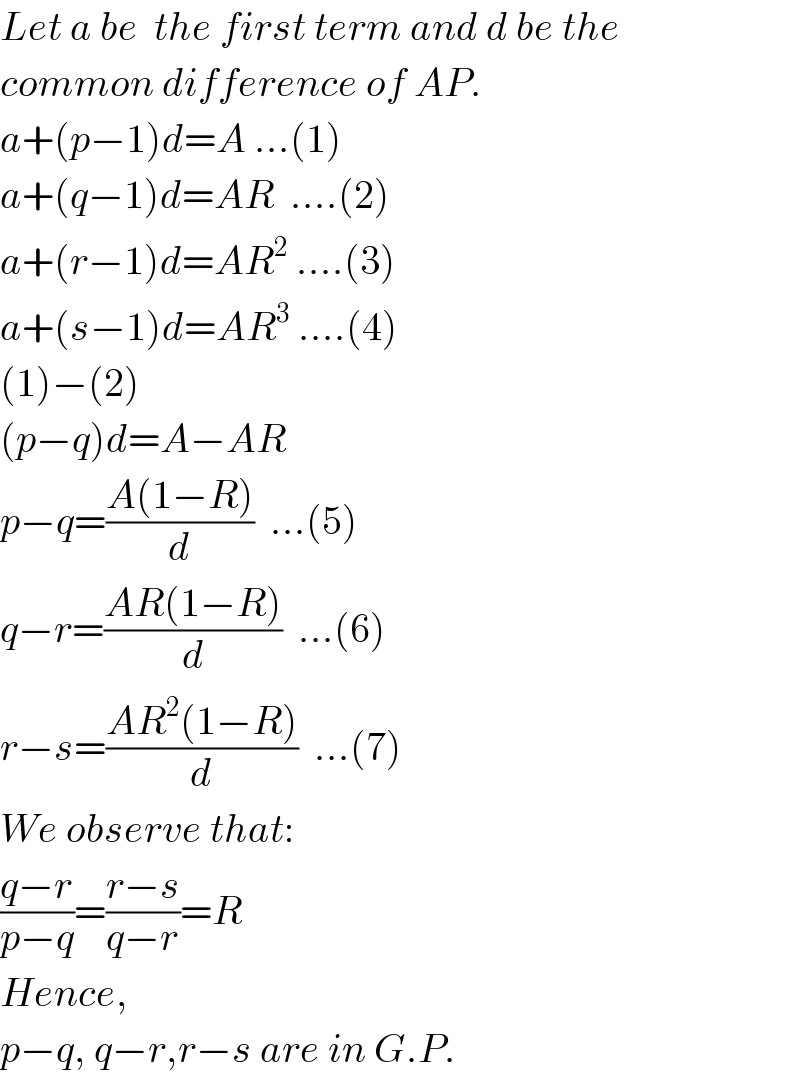
$${Let}\:{a}\:{be}\:\:{the}\:{first}\:{term}\:{and}\:{d}\:{be}\:{the} \\ $$$${common}\:{difference}\:{of}\:{AP}. \\ $$$${a}+\left({p}−\mathrm{1}\right){d}={A}\:...\left(\mathrm{1}\right) \\ $$$${a}+\left({q}−\mathrm{1}\right){d}={AR}\:\:....\left(\mathrm{2}\right) \\ $$$${a}+\left({r}−\mathrm{1}\right){d}={AR}^{\mathrm{2}} \:....\left(\mathrm{3}\right) \\ $$$${a}+\left({s}−\mathrm{1}\right){d}={AR}^{\mathrm{3}} \:....\left(\mathrm{4}\right) \\ $$$$\left(\mathrm{1}\right)−\left(\mathrm{2}\right) \\ $$$$\left({p}−{q}\right){d}={A}−{AR} \\ $$$${p}−{q}=\frac{{A}\left(\mathrm{1}−{R}\right)}{{d}}\:\:...\left(\mathrm{5}\right) \\ $$$${q}−{r}=\frac{{AR}\left(\mathrm{1}−{R}\right)}{{d}}\:\:...\left(\mathrm{6}\right) \\ $$$${r}−{s}=\frac{{AR}^{\mathrm{2}} \left(\mathrm{1}−{R}\right)}{{d}}\:\:...\left(\mathrm{7}\right) \\ $$$${We}\:{observe}\:{that}: \\ $$$$\frac{{q}−{r}}{{p}−{q}}=\frac{{r}−{s}}{{q}−{r}}={R} \\ $$$${Hence}, \\ $$$${p}−{q},\:{q}−{r},{r}−{s}\:{are}\:{in}\:{G}.{P}. \\ $$
Commented by peter frank last updated on 15/Sep/19

$${thank}\:\:{you} \\ $$
