
Question Number 68554 by Mikael last updated on 13/Sep/19
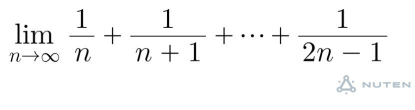
Commented by Prithwish sen last updated on 13/Sep/19
![lim_(n→∞) (1/n)[(1/(1+(0/n)))+ (1/(1+(1/n))) +......+(1/(1+((n−1)/n)))] =(1/n)Σ_(r=0) ^(n−1) lim _(n→∞) (1/(1+(r/n))) = ∫_0 ^1 (dx/(1+x)) = ln[1+x]_0 ^1](Q68558.png)
$$\mathrm{li}\underset{\mathrm{n}\rightarrow\infty} {\mathrm{m}}\frac{\mathrm{1}}{\mathrm{n}}\left[\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{0}}{\mathrm{n}}}+\:\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}}}\:+......+\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{n}−\mathrm{1}}{\mathrm{n}}}\right] \\ $$$$=\frac{\mathrm{1}}{\boldsymbol{\mathrm{n}}}\underset{\boldsymbol{\mathrm{r}}=\mathrm{0}} {\overset{\boldsymbol{\mathrm{n}}−\mathrm{1}} {\sum}}\:\:\boldsymbol{\mathrm{lim}}\underset{\boldsymbol{\mathrm{n}}\rightarrow\infty} {\:}\frac{\mathrm{1}}{\mathrm{1}+\frac{\boldsymbol{\mathrm{r}}}{\boldsymbol{\mathrm{n}}}}\:=\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{\boldsymbol{\mathrm{dx}}}{\mathrm{1}+\boldsymbol{\mathrm{x}}}\:=\:\boldsymbol{\mathrm{ln}}\left[\mathrm{1}+\boldsymbol{\mathrm{x}}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$
Commented by mathmax by abdo last updated on 13/Sep/19
![let A_n =(1/n)+(1/(n+1))+...+(1/(3n−1)) ⇒A_n =Σ_(k=0) ^(n−1) (1/(n+k)) =(1/n)Σ_(k=0) ^(n−1) (1/(1+(k/n))) so A_n is a Rieman sum ⇒lim_(n→+∞) A_n =∫_0 ^1 (dx/(1+x)) =[ln∣1+x∣]_0 ^1 =ln(2) .](Q68559.png)
$${let}\:{A}_{{n}} =\frac{\mathrm{1}}{{n}}+\frac{\mathrm{1}}{{n}+\mathrm{1}}+...+\frac{\mathrm{1}}{\mathrm{3}{n}−\mathrm{1}}\:\Rightarrow{A}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\frac{\mathrm{1}}{{n}+{k}} \\ $$$$=\frac{\mathrm{1}}{{n}}\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{1}+\frac{{k}}{{n}}}\:\:{so}\:{A}_{{n}} {is}\:{a}\:{Rieman}\:{sum}\:\Rightarrow{lim}_{{n}\rightarrow+\infty} {A}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dx}}{\mathrm{1}+{x}} \\ $$$$=\left[{ln}\mid\mathrm{1}+{x}\mid\right]_{\mathrm{0}} ^{\mathrm{1}} \:\:={ln}\left(\mathrm{2}\right)\:. \\ $$
Commented by Mikael last updated on 13/Sep/19
$${God}\:{bless}\:{you}\:{Sir}. \\ $$
Commented by mathmax by abdo last updated on 13/Sep/19
$${you}\:{are}\:{welcome}. \\ $$
