
Question Number 68537 by naka3546 last updated on 13/Sep/19

Answered by MJS last updated on 13/Sep/19

$$\mathrm{1}\:\mathrm{8}\:\mathrm{17} \\ $$$$\mathrm{4}\:\mathrm{7}\:\mathrm{17} \\ $$$$\mathrm{4}\:\mathrm{13}\:\mathrm{13} \\ $$$$\mathrm{7}\:\mathrm{7}\:\mathrm{16} \\ $$$$\mathrm{8}\:\mathrm{11}\:\mathrm{13} \\ $$
Commented by naka3546 last updated on 13/Sep/19
$${please}\:\:{show}\:\:{your}\:\:{workings} \\ $$
Commented by MJS last updated on 13/Sep/19
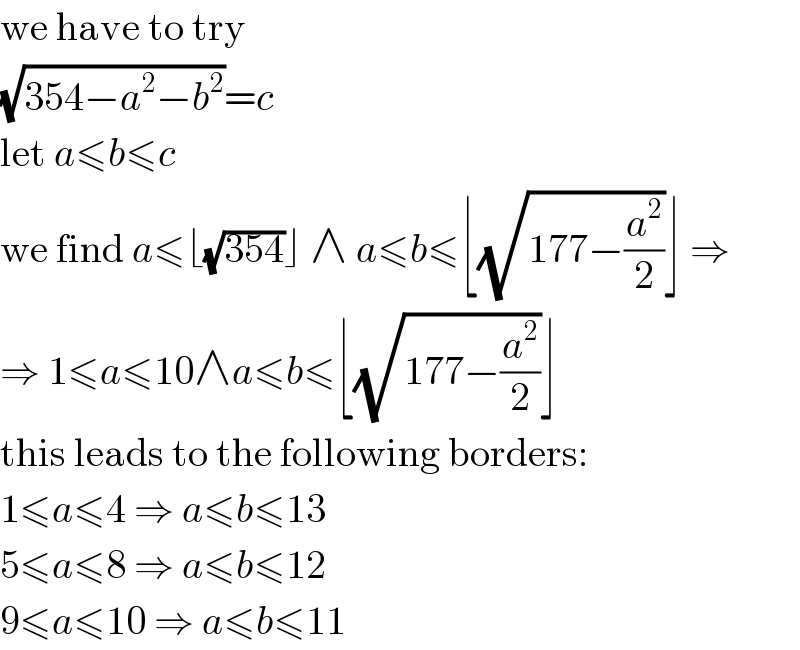
$$\mathrm{we}\:\mathrm{have}\:\mathrm{to}\:\mathrm{try} \\ $$$$\sqrt{\mathrm{354}−{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }={c} \\ $$$$\mathrm{let}\:{a}\leqslant{b}\leqslant{c} \\ $$$$\mathrm{we}\:\mathrm{find}\:{a}\leqslant\lfloor\sqrt{\mathrm{354}}\rfloor\:\wedge\:{a}\leqslant{b}\leqslant\lfloor\sqrt{\mathrm{177}−\frac{{a}^{\mathrm{2}} }{\mathrm{2}}}\rfloor\:\Rightarrow \\ $$$$\Rightarrow\:\mathrm{1}\leqslant{a}\leqslant\mathrm{10}\wedge{a}\leqslant{b}\leqslant\lfloor\sqrt{\mathrm{177}−\frac{{a}^{\mathrm{2}} }{\mathrm{2}}}\rfloor \\ $$$$\mathrm{this}\:\mathrm{leads}\:\mathrm{to}\:\mathrm{the}\:\mathrm{following}\:\mathrm{borders}: \\ $$$$\mathrm{1}\leqslant{a}\leqslant\mathrm{4}\:\Rightarrow\:{a}\leqslant{b}\leqslant\mathrm{13} \\ $$$$\mathrm{5}\leqslant{a}\leqslant\mathrm{8}\:\Rightarrow\:{a}\leqslant{b}\leqslant\mathrm{12} \\ $$$$\mathrm{9}\leqslant{a}\leqslant\mathrm{10}\:\Rightarrow\:{a}\leqslant{b}\leqslant\mathrm{11} \\ $$
Answered by Rasheed.Sindhi last updated on 18/Sep/19

$$\mathbb{A}\:\mathbb{D}\boldsymbol{\mathrm{ifferent}}\:\mathbb{W}\boldsymbol{\mathrm{ay}} \\ $$$$\mathrm{Can}\:\mathrm{be}\:\mathrm{proved}\:\mathrm{that}\:\mathrm{exactly}\:\boldsymbol{\mathrm{one}}\:\mathrm{of} \\ $$$$\mathrm{a},\mathrm{b}\:\&\:\mathrm{c}\:\mathrm{is}\:\mathrm{even}^{\bigstar} \:\mathrm{Also}\:\mathrm{1}\leqslant\mathrm{a},\mathrm{b},\mathrm{c}\leqslant\mathrm{18}. \\ $$$$\mathrm{Assume}\:\mathrm{that}\:\mathrm{a}\in\mathbb{E}\:\&\:\mathrm{b},\mathrm{c}\in\mathbb{O} \\ $$$$\mathrm{let}\:\mathrm{a}=\mathrm{2u},\mathrm{b}=\mathrm{2v}+\mathrm{1},\mathrm{c}=\mathrm{2w}+\mathrm{1} \\ $$$$\:\left(\mathrm{2u}\right)^{\mathrm{2}} +\left(\mathrm{2v}+\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{2w}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{354} \\ $$$$\:\:\mathrm{4u}^{\mathrm{2}} +\mathrm{4v}^{\mathrm{2}} +\mathrm{4v}+\mathrm{1}+\mathrm{4w}^{\mathrm{2}} +\mathrm{4w}+\mathrm{1}=\mathrm{354} \\ $$$$\:\:\mathrm{4u}^{\mathrm{2}} +\mathrm{4v}^{\mathrm{2}} +\mathrm{4v}+\mathrm{4w}^{\mathrm{2}} +\mathrm{4w}=\mathrm{352} \\ $$$$\:\:\:\:\:\mathrm{u}^{\mathrm{2}} +\mathrm{v}^{\mathrm{2}} +\mathrm{v}+\mathrm{w}^{\mathrm{2}} +\mathrm{w}=\mathrm{88} \\ $$$$\:\:\:\:\:\mathrm{u}^{\mathrm{2}} +\mathrm{v}\left(\mathrm{v}+\mathrm{1}\right)+\mathrm{w}\left(\mathrm{w}+\mathrm{1}\right)=\mathrm{88} \\ $$$$\:\:\:\:\mathrm{v}\left(\mathrm{v}+\mathrm{1}\right)\in\mathbb{E}\:\wedge\:\mathrm{w}\left(\mathrm{w}+\mathrm{1}\right)\in\mathbb{E} \\ $$$$\:\:\:\Rightarrow\mathrm{u}^{\mathrm{2}} \in\mathbb{E}\Rightarrow\mathrm{u}\in\mathbb{E}\Rightarrow\mathrm{a}=\mathrm{2u}\:\mathrm{is}\:\mathrm{doubly}\:\mathrm{even}. \\ $$$$\mathrm{Possible}\:\mathrm{values}\:\mathrm{for}\:\mathrm{a}:\:\mathrm{4},\mathrm{8},\mathrm{12}\:\&\:\mathrm{16} \\ $$$$\mathrm{For}\:\mathrm{a}=\mathrm{4}:\:\mathrm{c}=\sqrt{\mathrm{354}−\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} }=\sqrt{\mathrm{338}−\mathrm{b}^{\mathrm{2}} } \\ $$$$\:\:\:\:\mathrm{Possible}\:\mathrm{values}\:\mathrm{for}\:\mathrm{b}:\mathrm{1},\mathrm{3},\mathrm{5},...,\mathrm{17} \\ $$$$\:\:\:\:\mathrm{Only}\:\mathrm{for}\:\mathrm{b}=\mathrm{7},\mathrm{13}\:\&\:\mathrm{17};\:\mathrm{c}\in\mathbb{Z}^{+} \\ $$$$\:\:\:\:\mathrm{Successful}\:\mathrm{triplets}:\mathrm{4},\mathrm{7},\mathrm{17}\:\&\:\mathrm{4},\mathrm{13},\mathrm{13} \\ $$$$\mathrm{For}\:\mathrm{a}=\mathrm{8}:\mathrm{c}=\sqrt{\mathrm{354}−\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} }=\sqrt{\mathrm{290}−\mathrm{b}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\mathrm{Possible}\:\mathrm{values}\:\mathrm{for}\:\mathrm{b}:\mathrm{1},\mathrm{3},\mathrm{5},...,\mathrm{17} \\ $$$$\:\:\:\:\mathrm{Only}\:\mathrm{for}\:\mathrm{b}=\mathrm{1},\mathrm{11},\mathrm{13}\:\&\:\mathrm{17};\:\mathrm{c}\in\mathbb{Z}^{+} \\ $$$$\:\:\:\:\:\mathrm{Successful}\:\mathrm{triplets}:\mathrm{8},\mathrm{1},\mathrm{17}\:\&\:\mathrm{8},\mathrm{11},\mathrm{13} \\ $$$$\mathrm{For}\:\mathrm{a}=\mathrm{12}:\mathrm{c}=\sqrt{\mathrm{354}−\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} }=\sqrt{\mathrm{210}−\mathrm{b}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\mathrm{Possible}\:\mathrm{values}\:\mathrm{for}\:\mathrm{b}:\mathrm{1},\mathrm{3},\mathrm{5},...,\mathrm{13} \\ $$$$\:\:\:\:\:\mathrm{For}\:\boldsymbol{\mathrm{no}}\:\mathrm{value}\:\mathrm{of}\:\mathrm{b};\:\:\mathrm{c}\in\mathbb{Z}^{+} \\ $$$$\:\:\:\:\:\mathrm{No}\:\mathrm{Successful}\:\mathrm{triplets}. \\ $$$$\mathrm{For}\:\mathrm{a}=\mathrm{16}:\mathrm{c}=\sqrt{\mathrm{354}−\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} }=\sqrt{\mathrm{98}−\mathrm{b}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\mathrm{Possible}\:\mathrm{values}\:\mathrm{for}\:\mathrm{b}:\mathrm{1},\mathrm{3},\mathrm{5},...,\mathrm{9} \\ $$$$\:\:\:\:\mathrm{Only}\:\mathrm{for}\:\mathrm{b}=\mathrm{7}\:;\:\mathrm{c}\in\mathbb{Z}^{+} \\ $$$$\:\:\:\:\:\mathrm{Successful}\:\mathrm{triplets}:\mathrm{16},\mathrm{7},\mathrm{7} \\ $$$$ \\ $$
Commented by Rasheed.Sindhi last updated on 14/Sep/19
![^★ a^2 +b^2 +c^2 =354⇒a^2 +b^2 +c^2 ∈E ^• a,b,c all are not odd.If they were a^2 +b^2 +c^(2 ) be surely odd. ^• a,b,c all are not even:If they were a^2 +b^2 +c^(2 ) were doubly even but it is not because it is equal to a singly even(354) [a^2 +b^2 +c^2 =(2u)^2 +(2v)^2 +(2w)^2 =4(u^2 +v^2 +w^2 )] ^• Two of a,b,c can′t be even.If they were , a^2 +b^2 +c^2 be odd due to one odd. ^• ∴ only one of a,b,c is even.](Q68586.png)
$$\:^{\bigstar} \mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} =\mathrm{354}\Rightarrow\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} \in\mathbb{E} \\ $$$$\:\:^{\bullet} \mathrm{a},\mathrm{b},\mathrm{c}\:\mathrm{all}\:\mathrm{are}\:\mathrm{not}\:\mathrm{odd}.\mathrm{If}\:\mathrm{they}\:\mathrm{were} \\ $$$$\:\:\:\:\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}\:} \mathrm{be}\:\mathrm{surely}\:\mathrm{odd}. \\ $$$$\:\:^{\bullet} \mathrm{a},\mathrm{b},\mathrm{c}\:\mathrm{all}\:\mathrm{are}\:\mathrm{not}\:\mathrm{even}:\mathrm{If}\:\mathrm{they}\:\mathrm{were} \\ $$$$\:\:\:\:\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}\:} \mathrm{were}\:\mathrm{doubly}\:\mathrm{even}\:\mathrm{but} \\ $$$$\:\:\:\:\mathrm{it}\:\mathrm{is}\:\mathrm{not}\:\mathrm{because}\:\mathrm{it}\:\mathrm{is}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{a}\:\mathrm{singly} \\ $$$$\:\:\:\:\:\mathrm{even}\left(\mathrm{354}\right) \\ $$$$\:\:\:\:\:\left[\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} =\left(\mathrm{2u}\right)^{\mathrm{2}} +\left(\mathrm{2v}\right)^{\mathrm{2}} +\left(\mathrm{2w}\right)^{\mathrm{2}} \right. \\ $$$$\left.\:\:\:\:\:\:\:=\mathrm{4}\left(\mathrm{u}^{\mathrm{2}} +\mathrm{v}^{\mathrm{2}} +\mathrm{w}^{\mathrm{2}} \right)\right] \\ $$$$\:\:^{\bullet} \mathrm{Two}\:\mathrm{of}\:\mathrm{a},\mathrm{b},\mathrm{c}\:\mathrm{can}'\mathrm{t}\:\mathrm{be}\:\mathrm{even}.\mathrm{If}\:\mathrm{they} \\ $$$$\:\:\:\:\:\mathrm{were}\:,\:\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} \:\mathrm{be}\:\mathrm{odd}\:\mathrm{due}\:\mathrm{to}\:\mathrm{one} \\ $$$$\:\:\:\:\:\mathrm{odd}. \\ $$$$\:\:^{\bullet} \therefore\:\mathrm{only}\:\mathrm{one}\:\mathrm{of}\:\mathrm{a},\mathrm{b},\mathrm{c}\:\mathrm{is}\:\mathrm{even}. \\ $$
