
Question Number 68510 by oyemi kemewari last updated on 12/Sep/19
Answered by mr W last updated on 14/Sep/19
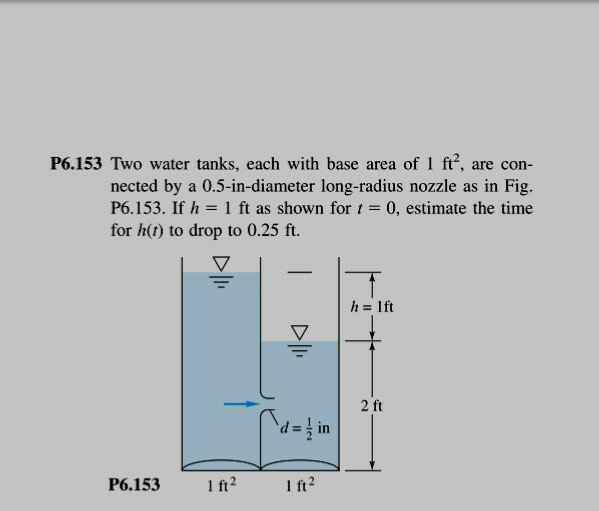
![v=(√(2gh)) base area of tanks=A=1 ft^2 A(dh/2)=−((πd^2 )/4)vdt dh=−((πd^2 (√(2gh)))/(2A))dt (dh/(√h))=−((πd^2 (√(2g)))/(2A))dt ∫_h_0 ^h (dh/(√h))=−((πd^2 (√(2g)))/(2A))∫_0 ^t dt 2[(√h)−(√h_0 )]=−((πd^2 (√(2g)))/(2A))t (√h_0 )−(√h)=((πd^2 (√(2g)))/(4A))t ⇒t=((4A((√h_0 )−(√h)))/(πd^2 (√(2g)))) h_0 =1 ft d=0.5 in=(1/(24)) ft for h=0.25 ft: t=((4×1((√1)−(√(0.25))))/(π((1/(24)))^2 (√(2g))))=82 seconds for h=0: t=((4×1((√1)−(√0)))/(π((1/(24)))^2 (√(2g))))=164 seconds](Q68630.png)
$${v}=\sqrt{\mathrm{2}{gh}} \\ $$$${base}\:{area}\:{of}\:{tanks}={A}=\mathrm{1}\:{ft}^{\mathrm{2}} \\ $$$${A}\frac{{dh}}{\mathrm{2}}=−\frac{\pi{d}^{\mathrm{2}} }{\mathrm{4}}{vdt} \\ $$$${dh}=−\frac{\pi{d}^{\mathrm{2}} \sqrt{\mathrm{2}{gh}}}{\mathrm{2}{A}}{dt} \\ $$$$\frac{{dh}}{\sqrt{{h}}}=−\frac{\pi{d}^{\mathrm{2}} \sqrt{\mathrm{2}{g}}}{\mathrm{2}{A}}{dt} \\ $$$$\int_{{h}_{\mathrm{0}} } ^{{h}} \frac{{dh}}{\sqrt{{h}}}=−\frac{\pi{d}^{\mathrm{2}} \sqrt{\mathrm{2}{g}}}{\mathrm{2}{A}}\int_{\mathrm{0}} ^{{t}} {dt} \\ $$$$\mathrm{2}\left[\sqrt{{h}}−\sqrt{{h}_{\mathrm{0}} }\right]=−\frac{\pi{d}^{\mathrm{2}} \sqrt{\mathrm{2}{g}}}{\mathrm{2}{A}}{t} \\ $$$$\sqrt{{h}_{\mathrm{0}} }−\sqrt{{h}}=\frac{\pi{d}^{\mathrm{2}} \sqrt{\mathrm{2}{g}}}{\mathrm{4}{A}}{t} \\ $$$$\Rightarrow{t}=\frac{\mathrm{4}{A}\left(\sqrt{{h}_{\mathrm{0}} }−\sqrt{{h}}\right)}{\pi{d}^{\mathrm{2}} \sqrt{\mathrm{2}{g}}} \\ $$$${h}_{\mathrm{0}} =\mathrm{1}\:{ft} \\ $$$${d}=\mathrm{0}.\mathrm{5}\:{in}=\frac{\mathrm{1}}{\mathrm{24}}\:{ft} \\ $$$$ \\ $$$${for}\:{h}=\mathrm{0}.\mathrm{25}\:{ft}: \\ $$$${t}=\frac{\mathrm{4}×\mathrm{1}\left(\sqrt{\mathrm{1}}−\sqrt{\mathrm{0}.\mathrm{25}}\right)}{\pi\left(\frac{\mathrm{1}}{\mathrm{24}}\right)^{\mathrm{2}} \sqrt{\mathrm{2}{g}}}=\mathrm{82}\:{seconds} \\ $$$$ \\ $$$${for}\:{h}=\mathrm{0}: \\ $$$${t}=\frac{\mathrm{4}×\mathrm{1}\left(\sqrt{\mathrm{1}}−\sqrt{\mathrm{0}}\right)}{\pi\left(\frac{\mathrm{1}}{\mathrm{24}}\right)^{\mathrm{2}} \sqrt{\mathrm{2}{g}}}=\mathrm{164}\:{seconds} \\ $$
Commented by mr W last updated on 14/Sep/19
Commented by oyemi kemewari last updated on 17/Sep/19

$$ \\ $$
Commented by oyemi kemewari last updated on 28/Sep/19
thank you sir
