
Question Number 68451 by mr W last updated on 10/Sep/19
Commented by mr W last updated on 11/Sep/19
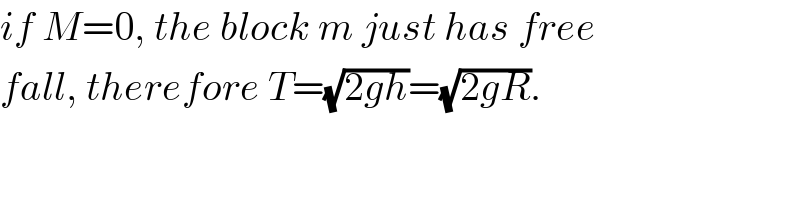
$${if}\:{M}=\mathrm{0},\:{the}\:{block}\:{m}\:{just}\:{has}\:{free} \\ $$$${fall},\:{therefore}\:{T}=\sqrt{\mathrm{2}{gh}}=\sqrt{\mathrm{2}{gR}}. \\ $$
Commented by ajfour last updated on 11/Sep/19

$${sorry}\:{sir}\:{my}\:{mistake}\:{first}, \\ $$$${it}\:{matched}\:{but}\:{in}\:{the}\:{end}\:{i} \\ $$$${typed}\:{in}\:\sqrt{\mathrm{2}{gR}}\:\:{it}\:{is}\:{time}\:{not} \\ $$$${velocity}\:\:{it}\:{is}\:\sqrt{\frac{\mathrm{2}{R}}{{g}}}\:\:\:\left({ha}..{ha}\right) \\ $$$${By}\:{the}\:{way}\:{please}\:{check},\:{i}\:{got} \\ $$$${some}\:{answer}\:{for}\:{fixed}\:{wedge}\:{too}. \\ $$
Commented by mr W last updated on 10/Sep/19

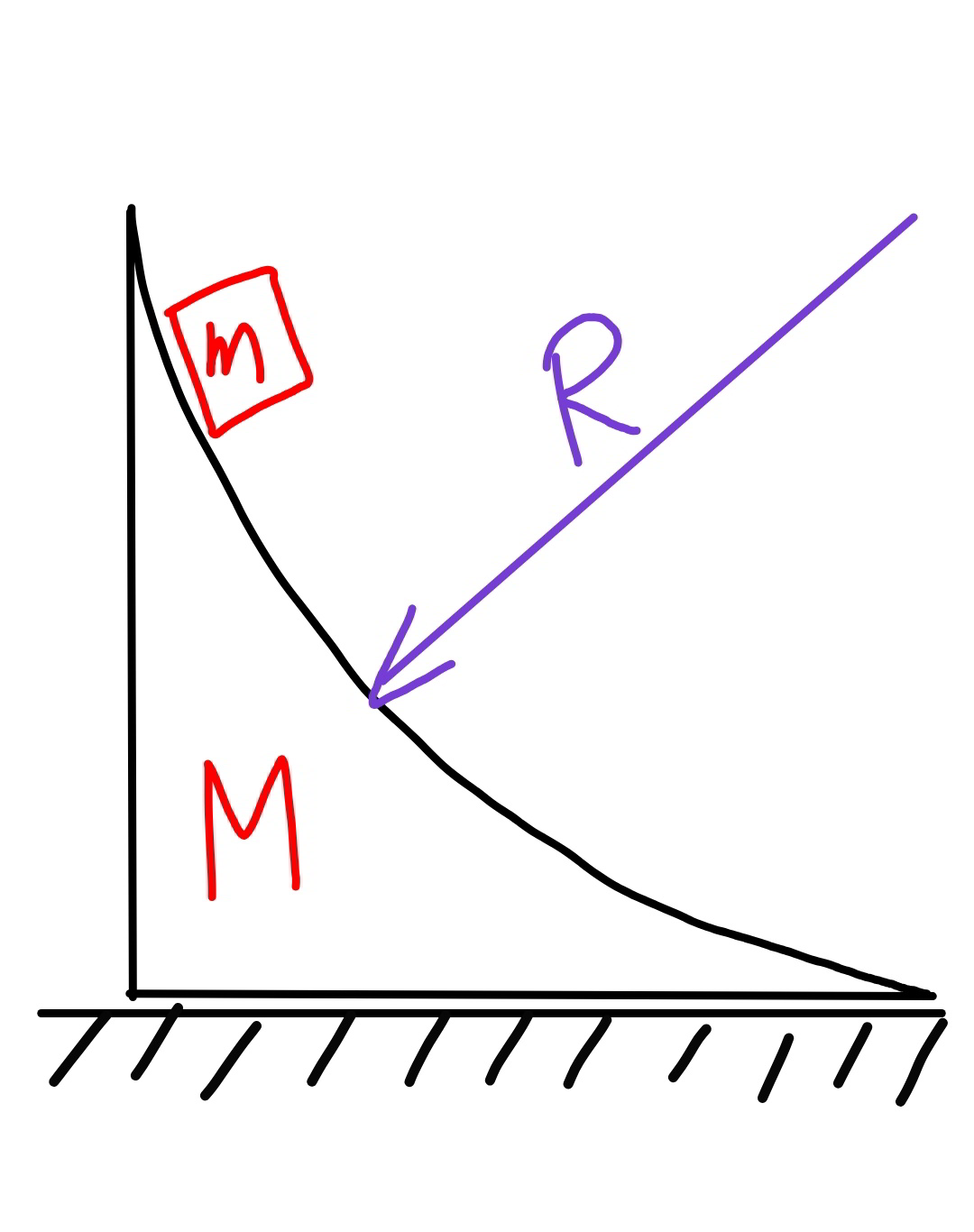
$${the}\:{block}\:{m}\:{is}\:{released}\:{at}\:{the}\:{top}\:{of} \\ $$$${the}\:{wedge}.\:{there}\:{is}\:{no}\:{friction}. \\ $$$$ \\ $$$${find}\:{the}\:{velocity}\:{of}\:{both}\:{objects}\:{when} \\ $$$${the}\:{small}\:{block}\:{reaches}\:{the}\:{bottom} \\ $$$${of}\:{the}\:{wedge}. \\ $$
Commented by ajfour last updated on 11/Sep/19
Commented by ajfour last updated on 11/Sep/19
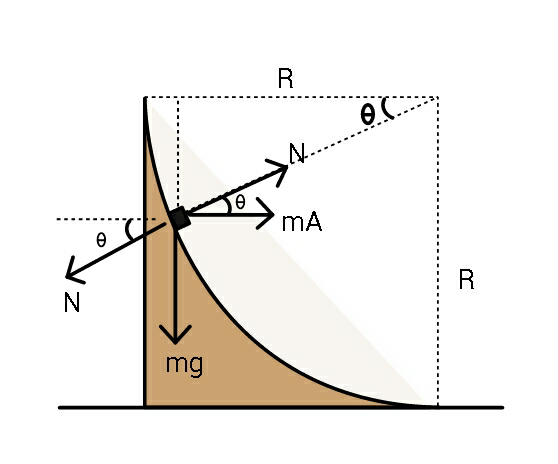
![Lets try and find time it takes to slip down. N+mAcos θ−mgsin θ=((mv_r ^2 )/R) mAsin θ+mgcos θ=((mv_r dv_r )/(Rdθ)) Ncos θ=MA ⇒ if we let M=μm μAsec θ+Acos θ−gsin θ=(v_r ^2 /R) ..(i) Asin θ+gcos θ=((v_r dv_r )/(Rdθ)) ⇒ A=(((v_r dv_r )/(Rdθ))−gcos θ)cosec θ ...(ii) ⇒ (μsec θ+cos θ)(((v_r dv_r )/(Rdθ))−gcos θ)cosec θ −gsin θ=(v_r ^2 /R) let v_r ^2 /R=2s ⇒ v_r dv_r /R=ds Now (μsec θ+cos θ)(cosec θ)(ds/dθ)−2s = gsin θ+gcos θcosec θ(μsec θ+cos θ) or (ds/dθ)−((2s(sin θ))/((μsec θ+cos θ))) =g(((sin^2 θ)/(μsec θ+cos θ))+cos θ) ⇒ (ds/(cos θdθ))−((2s(sin θ))/((μ+cos^2 θ))) =g(1+((sin^2 θ)/(μ+cos^2 θ))) let sin θ=u ⇒ cos θdθ=du ⇒ (ds/du)−((2su)/(μ+1−u^2 ))=((g(μ+1))/(μ+1−u^2 )) let μ+1=λ ⇒ (ds/du)+((2su)/(u^2 −λ))=((λg)/(λ−u^2 )) ⇒ (u^2 −λ)(ds/du)+2su=−λg ⇒ ∫_0 ^( s(u^2 −λ)) d[s(u^2 −λ)]=−λg∫_0 ^( u) du ⇒ s(u^2 −λ)=−λgu ⇒ [ (v_r ^2 /(2R))(sin^2 θ−λ)=−λgsin θ] but if we continue with same variable u=sin θ, then ⇒ v_r =((d(Rdθ))/dt)=(√(2sR)) = (√(2R(((λgu)/(λ−u^2 ))))) ∫_0 ^( T) dt =∫_0 ^( 1) ((Rdu)/(√(1−u^2 )))(√((λ−u^2 )/(2λgRu))) T=(√(R/(2λg)))∫_0 ^( 1) (√((λ−u^2 )/(u(1−u^2 )))) du If wedge is far too heavier, then it is as good as fixed; μ=(M/m)→∞ T=(√(R/(2g)))∫_0 ^( 1) (du/(√(u(1−u^2 )))) =t_0 ∫_0 ^( π/2) ((cos θdθ)/(√(sin θcos^2 θ))) =t_0 ∫_0 ^( π/2) (dθ/(√(sin θ))) let sin θ=t^2 ⇒ 2tdt=cos θdθ ⇒ dθ=((2tdt)/(√(1−t^2 ))) T=t_0 ∫_0 ^( 1) ((2tdt)/(t(√(1−t^2 )))) = 2t_0 ∫_0 ^( 1) (dt/(√(1−t^2 ))) =2t_0 ((π/2)) =πt_0 T=π(√(R/(2g))) ! If there is a very light wedge (just to check) μ=(M/m) →0 ⇒ λ→1 T=(√(R/(2g)))∫_0 ^( 1) (du/(√u)) T= (√((2R)/g)) (fabulous!) but i think otherwise solving the integration is beyond my understanding..](Q68480.png)
$${Lets}\:{try}\:{and}\:{find}\:{time}\:{it}\:{takes} \\ $$$${to}\:{slip}\:{down}. \\ $$$${N}+{mA}\mathrm{cos}\:\theta−{mg}\mathrm{sin}\:\theta=\frac{{mv}_{{r}} ^{\mathrm{2}} }{{R}} \\ $$$${mA}\mathrm{sin}\:\theta+{mg}\mathrm{cos}\:\theta=\frac{{mv}_{{r}} {dv}_{{r}} }{{Rd}\theta} \\ $$$${N}\mathrm{cos}\:\theta={MA} \\ $$$$\Rightarrow\:\:{if}\:{we}\:{let}\:{M}=\mu{m} \\ $$$$\mu{A}\mathrm{sec}\:\theta+{A}\mathrm{cos}\:\theta−{g}\mathrm{sin}\:\theta=\frac{{v}_{{r}} ^{\mathrm{2}} }{{R}}\:\:\:\:..\left({i}\right) \\ $$$${A}\mathrm{sin}\:\theta+{g}\mathrm{cos}\:\theta=\frac{{v}_{{r}} {dv}_{{r}} }{{Rd}\theta} \\ $$$$\Rightarrow\:{A}=\left(\frac{{v}_{{r}} {dv}_{{r}} }{{Rd}\theta}−{g}\mathrm{cos}\:\theta\right)\mathrm{cosec}\:\theta\:\:...\left({ii}\right) \\ $$$$\Rightarrow \\ $$$$\left(\mu\mathrm{sec}\:\theta+\mathrm{cos}\:\theta\right)\left(\frac{{v}_{{r}} {dv}_{{r}} }{{Rd}\theta}−{g}\mathrm{cos}\:\theta\right)\mathrm{cosec}\:\theta \\ $$$$\:\:\:−{g}\mathrm{sin}\:\theta=\frac{{v}_{{r}} ^{\mathrm{2}} }{{R}} \\ $$$${let}\:\:{v}_{{r}} ^{\mathrm{2}} /{R}=\mathrm{2}{s}\:\:\Rightarrow\:{v}_{{r}} {dv}_{{r}} /{R}={ds} \\ $$$${Now} \\ $$$$\:\left(\mu\mathrm{sec}\:\theta+\mathrm{cos}\:\theta\right)\left(\mathrm{cosec}\:\theta\right)\frac{{ds}}{{d}\theta}−\mathrm{2}{s} \\ $$$$\:\:=\:{g}\mathrm{sin}\:\theta+{g}\mathrm{cos}\:\theta\mathrm{cosec}\:\theta\left(\mu\mathrm{sec}\:\theta+\mathrm{cos}\:\theta\right) \\ $$$${or} \\ $$$$\frac{{ds}}{{d}\theta}−\frac{\mathrm{2}{s}\left(\mathrm{sin}\:\theta\right)}{\left(\mu\mathrm{sec}\:\theta+\mathrm{cos}\:\theta\right)} \\ $$$$\:\:\:\:\:\:\:\:\:={g}\left(\frac{\mathrm{sin}\:^{\mathrm{2}} \theta}{\mu\mathrm{sec}\:\theta+\mathrm{cos}\:\theta}+\mathrm{cos}\:\theta\right) \\ $$$$\Rightarrow \\ $$$$\frac{{ds}}{\mathrm{cos}\:\theta{d}\theta}−\frac{\mathrm{2}{s}\left(\mathrm{sin}\:\theta\right)}{\left(\mu+\mathrm{cos}\:^{\mathrm{2}} \theta\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:={g}\left(\mathrm{1}+\frac{\mathrm{sin}\:^{\mathrm{2}} \theta}{\mu+\mathrm{cos}\:^{\mathrm{2}} \theta}\right) \\ $$$${let}\:\:\mathrm{sin}\:\theta={u}\:\:\Rightarrow\:\:\mathrm{cos}\:\theta{d}\theta={du} \\ $$$$\Rightarrow \\ $$$$\:\:\frac{{ds}}{{du}}−\frac{\mathrm{2}{su}}{\mu+\mathrm{1}−{u}^{\mathrm{2}} }=\frac{{g}\left(\mu+\mathrm{1}\right)}{\mu+\mathrm{1}−{u}^{\mathrm{2}} } \\ $$$${let}\:\:\mu+\mathrm{1}=\lambda\:\:\:\Rightarrow \\ $$$$\:\:\frac{{ds}}{{du}}+\frac{\mathrm{2}{su}}{{u}^{\mathrm{2}} −\lambda}=\frac{\lambda{g}}{\lambda−{u}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\:\left({u}^{\mathrm{2}} −\lambda\right)\frac{{ds}}{{du}}+\mathrm{2}{su}=−\lambda{g} \\ $$$$\Rightarrow\:\int_{\mathrm{0}} ^{\:{s}\left({u}^{\mathrm{2}} −\lambda\right)} {d}\left[{s}\left({u}^{\mathrm{2}} −\lambda\right)\right]=−\lambda{g}\int_{\mathrm{0}} ^{\:{u}} {du} \\ $$$$\Rightarrow\:{s}\left({u}^{\mathrm{2}} −\lambda\right)=−\lambda{gu} \\ $$$$\Rightarrow\:\left[\:\frac{{v}_{{r}} ^{\mathrm{2}} }{\mathrm{2}{R}}\left(\mathrm{sin}\:^{\mathrm{2}} \theta−\lambda\right)=−\lambda{g}\mathrm{sin}\:\theta\right] \\ $$$${but}\:{if}\:{we}\:{continue}\:{with}\:{same} \\ $$$${variable}\:{u}=\mathrm{sin}\:\theta,\:{then} \\ $$$$\Rightarrow\:{v}_{{r}} =\frac{{d}\left({Rd}\theta\right)}{{dt}}=\sqrt{\mathrm{2}{sR}}\:=\:\sqrt{\mathrm{2}{R}\left(\frac{\lambda{gu}}{\lambda−{u}^{\mathrm{2}} }\right)} \\ $$$$\int_{\mathrm{0}} ^{\:\:{T}} {dt}\:=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{Rdu}}{\sqrt{\mathrm{1}−{u}^{\mathrm{2}} }}\sqrt{\frac{\lambda−{u}^{\mathrm{2}} }{\mathrm{2}\lambda{gRu}}} \\ $$$${T}=\sqrt{\frac{{R}}{\mathrm{2}\lambda{g}}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \sqrt{\frac{\lambda−{u}^{\mathrm{2}} }{{u}\left(\mathrm{1}−{u}^{\mathrm{2}} \right)}}\:{du} \\ $$$${If}\:{wedge}\:{is}\:{far}\:{too}\:{heavier},\:{then} \\ $$$${it}\:{is}\:{as}\:{good}\:{as}\:{fixed}; \\ $$$$\mu=\frac{{M}}{{m}}\rightarrow\infty \\ $$$${T}=\sqrt{\frac{{R}}{\mathrm{2}{g}}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{du}}{\sqrt{{u}\left(\mathrm{1}−{u}^{\mathrm{2}} \right)}} \\ $$$$\:\:\:\:={t}_{\mathrm{0}} \int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \frac{\mathrm{cos}\:\theta{d}\theta}{\sqrt{\mathrm{sin}\:\theta\mathrm{cos}\:^{\mathrm{2}} \theta}} \\ $$$$\:\:\:\:={t}_{\mathrm{0}} \int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \frac{{d}\theta}{\sqrt{\mathrm{sin}\:\theta}}\:\:\:{let}\:\mathrm{sin}\:\theta={t}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\mathrm{2}{tdt}=\mathrm{cos}\:\theta{d}\theta \\ $$$$\Rightarrow\:\:\:{d}\theta=\frac{\mathrm{2}{tdt}}{\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }} \\ $$$$\:\:\:{T}={t}_{\mathrm{0}} \int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{2}{tdt}}{{t}\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}\:=\:\mathrm{2}{t}_{\mathrm{0}} \int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{dt}}{\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }} \\ $$$$\:\:\:\:\:=\mathrm{2}{t}_{\mathrm{0}} \left(\frac{\pi}{\mathrm{2}}\right)\:=\pi{t}_{\mathrm{0}} \\ $$$$\:\:{T}=\pi\sqrt{\frac{{R}}{\mathrm{2}{g}}}\:\:! \\ $$$${If}\:{there}\:{is}\:{a}\:{very}\:{light}\:{wedge} \\ $$$$\:\:\:\left({just}\:{to}\:{check}\right) \\ $$$$\mu=\frac{{M}}{{m}}\:\rightarrow\mathrm{0}\:\Rightarrow\:\lambda\rightarrow\mathrm{1} \\ $$$${T}=\sqrt{\frac{{R}}{\mathrm{2}{g}}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\frac{{du}}{\sqrt{{u}}}\:\:\: \\ $$$$\:\:{T}=\:\sqrt{\frac{\mathrm{2}{R}}{{g}}}\:\:\left({fabulous}!\right) \\ $$$${but}\:{i}\:{think}\:{otherwise}\:{solving}\:{the}\: \\ $$$${integration}\:{is}\:{beyond}\:{my} \\ $$$${understanding}.. \\ $$$$ \\ $$
Commented by mr W last updated on 11/Sep/19
$${thanks}\:{sir}\:{for}\:{solving}! \\ $$$${can}\:{we}\:{find}\:{the}\:{time}\:{if}\:{the}\:{wedge}\:{is} \\ $$$${fixed}\:{on}\:{the}\:{ground}? \\ $$
Commented by mr W last updated on 11/Sep/19
$${fantastic}\:{sir}!\:{correct}\:{result}. \\ $$
Answered by ajfour last updated on 10/Sep/19
![mgR=(1/2)mv^2 +(1/2)MV^( 2) mv=MV 2mgR=[m+M((m/M))^2 ]v^2 v=(√((2MgR)/(M+m))) , V=(√((2mgR)/(M+m))) .](Q68459.png)
$${mgR}=\frac{\mathrm{1}}{\mathrm{2}}{mv}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{MV}^{\:\mathrm{2}} \\ $$$${mv}={MV} \\ $$$$\mathrm{2}{mgR}=\left[{m}+{M}\left(\frac{{m}}{{M}}\right)^{\mathrm{2}} \right]{v}^{\mathrm{2}} \\ $$$${v}=\sqrt{\frac{\mathrm{2}{MgR}}{{M}+{m}}}\:\:\:\:,\:\:{V}=\sqrt{\frac{\mathrm{2}{mgR}}{{M}+{m}}}\:. \\ $$
Commented by mr W last updated on 11/Sep/19
$${simple}\:{and}\:{direct},\:{great}! \\ $$
