Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 68210 by peter frank last updated on 07/Sep/19

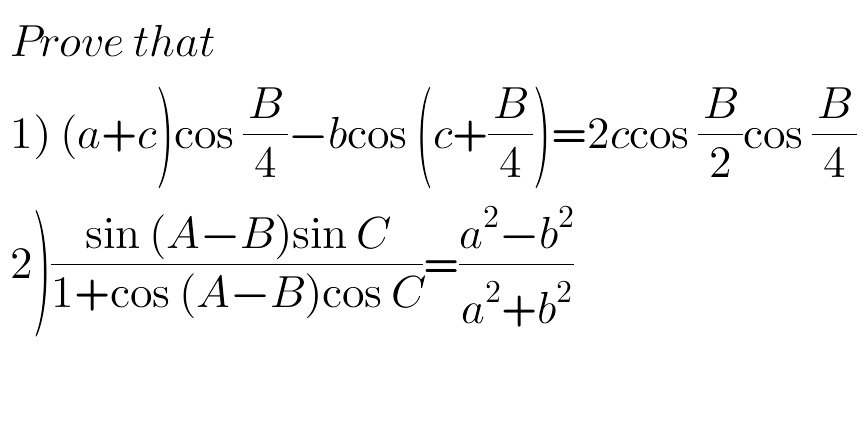
Answered by $@ty@m123 last updated on 08/Sep/19

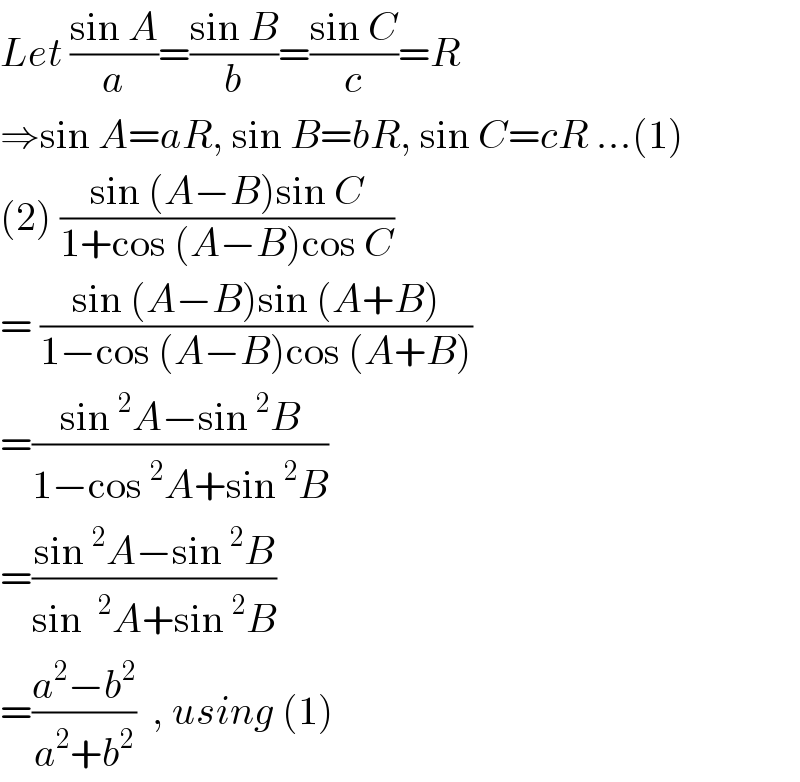
Let ((sin A)/a)=((sin B)/b)=((sin C)/c)=R ⇒sin A=aR, sin B=bR, sin C=cR ...(1) (2) ((sin (A−B)sin C)/(1+cos (A−B)cos C)) = ((sin (A−B)sin (A+B))/(1−cos (A−B)cos (A+B))) =((sin^2 A−sin^2 B)/(1−cos^2 A+sin^2 B)) =((sin^2 A−sin^2 B)/(sin ^2 A+sin^2 B)) =((a^2 −b^2 )/(a^2 +b^2 )) , using (1)

$${Let}\:\frac{\mathrm{sin}\:{A}}{{a}}=\frac{\mathrm{sin}\:{B}}{{b}}=\frac{\mathrm{sin}\:{C}}{{c}}={R} \\ $$$$\Rightarrow\mathrm{sin}\:{A}={aR},\:\mathrm{sin}\:{B}={bR},\:\mathrm{sin}\:{C}={cR}\:...\left(\mathrm{1}\right) \\ $$$$\left(\mathrm{2}\right)\:\frac{\mathrm{sin}\:\left({A}−{B}\right)\mathrm{sin}\:{C}}{\mathrm{1}+\mathrm{cos}\:\left({A}−{B}\right)\mathrm{cos}\:{C}} \\ $$$$=\:\frac{\mathrm{sin}\:\left({A}−{B}\right)\mathrm{sin}\:\left({A}+{B}\right)}{\mathrm{1}−\mathrm{cos}\:\left({A}−{B}\right)\mathrm{cos}\:\left({A}+{B}\right)} \\ $$$$=\frac{\mathrm{sin}\:^{\mathrm{2}} {A}−\mathrm{sin}\:^{\mathrm{2}} {B}}{\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} {A}+\mathrm{sin}\:^{\mathrm{2}} {B}} \\ $$$$=\frac{\mathrm{sin}\:^{\mathrm{2}} {A}−\mathrm{sin}\:^{\mathrm{2}} {B}}{\mathrm{sin}\:\:^{\mathrm{2}} {A}+\mathrm{sin}\:^{\mathrm{2}} {B}} \\ $$$$=\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\:\:,\:{using}\:\left(\mathrm{1}\right) \\ $$

Commented by peter frank last updated on 08/Sep/19

thanks for solvinv sir

$${thanks}\:{for}\:{solvinv}\:{sir} \\ $$

Commented by $@ty@m123 last updated on 09/Sep/19

You′re welcome. Meanwhile trying for (1)

$${You}'{re}\:{welcome}. \\ $$$${Meanwhile}\:{trying}\:{for}\:\left(\mathrm{1}\right) \\ $$

Answered by $@ty@m123 last updated on 10/Sep/19

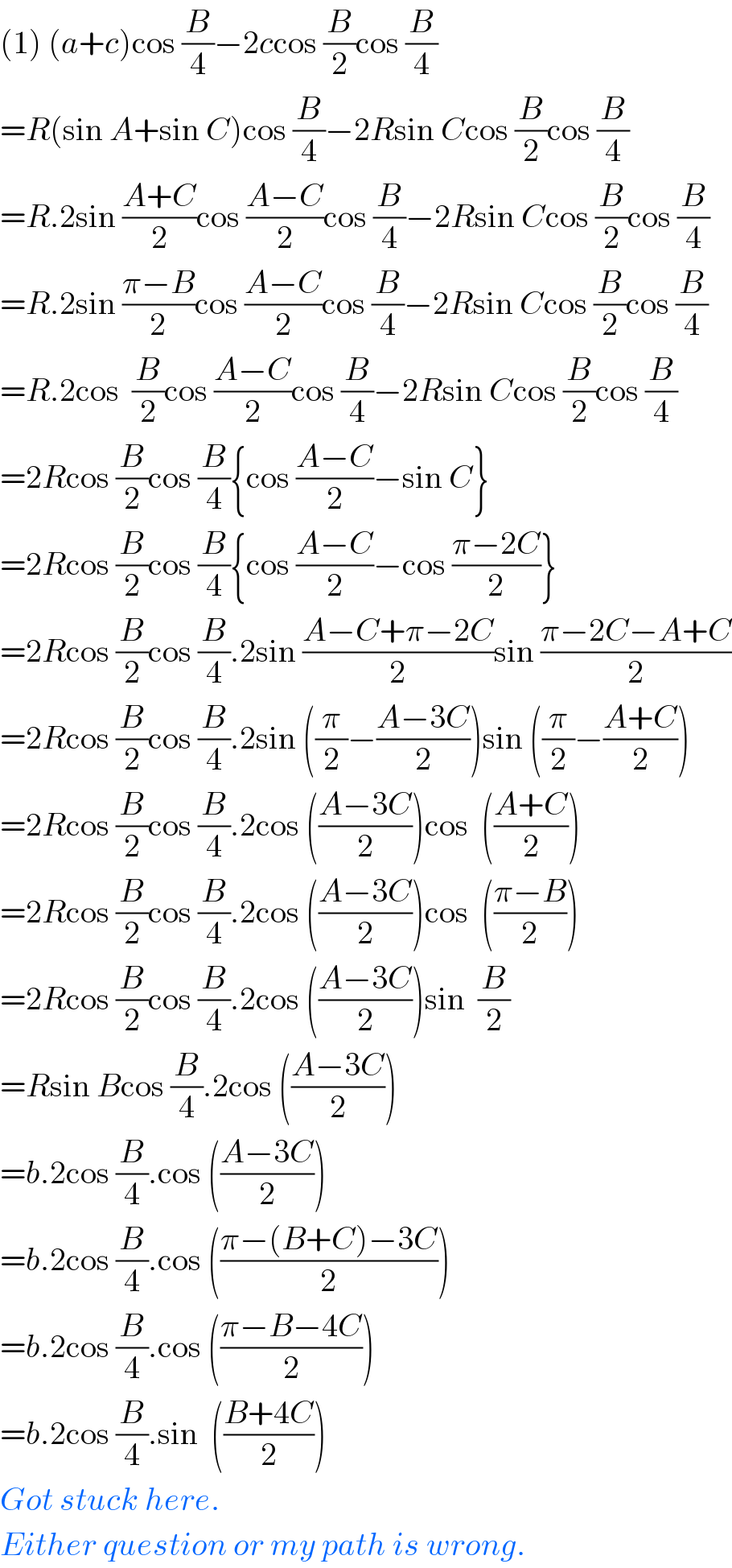
(1) (a+c)cos (B/4)−2ccos (B/2)cos (B/4) =R(sin A+sin C)cos (B/4)−2Rsin Ccos (B/2)cos (B/4) =R.2sin ((A+C)/2)cos ((A−C)/2)cos (B/4)−2Rsin Ccos (B/2)cos (B/4) =R.2sin ((π−B)/2)cos ((A−C)/2)cos (B/4)−2Rsin Ccos (B/2)cos (B/4) =R.2cos (B/2)cos ((A−C)/2)cos (B/4)−2Rsin Ccos (B/2)cos (B/4) =2Rcos (B/2)cos (B/4){cos ((A−C)/2)−sin C} =2Rcos (B/2)cos (B/4){cos ((A−C)/2)−cos ((π−2C)/2)} =2Rcos (B/2)cos (B/4).2sin ((A−C+π−2C)/2)sin ((π−2C−A+C)/2) =2Rcos (B/2)cos (B/4).2sin ((π/2)−((A−3C)/2))sin ((π/2)−((A+C)/2)) =2Rcos (B/2)cos (B/4).2cos (((A−3C)/2))cos (((A+C)/2)) =2Rcos (B/2)cos (B/4).2cos (((A−3C)/2))cos (((π−B)/2)) =2Rcos (B/2)cos (B/4).2cos (((A−3C)/2))sin (B/2) =Rsin Bcos (B/4).2cos (((A−3C)/2)) =b.2cos (B/4).cos (((A−3C)/2)) =b.2cos (B/4).cos (((π−(B+C)−3C)/2)) =b.2cos (B/4).cos (((π−B−4C)/2)) =b.2cos (B/4).sin (((B+4C)/2)) Got stuck here. Either question or my path is wrong.

$$\left(\mathrm{1}\right)\:\left({a}+{c}\right)\mathrm{cos}\:\frac{{B}}{\mathrm{4}}−\mathrm{2}{c}\mathrm{cos}\:\frac{{B}}{\mathrm{2}}\mathrm{cos}\:\frac{{B}}{\mathrm{4}} \\ $$$$={R}\left(\mathrm{sin}\:{A}+\mathrm{sin}\:{C}\right)\mathrm{cos}\:\frac{{B}}{\mathrm{4}}−\mathrm{2}{R}\mathrm{sin}\:{C}\mathrm{cos}\:\frac{{B}}{\mathrm{2}}\mathrm{cos}\:\frac{{B}}{\mathrm{4}} \\ $$$$={R}.\mathrm{2sin}\:\frac{{A}+{C}}{\mathrm{2}}\mathrm{cos}\:\frac{{A}−{C}}{\mathrm{2}}\mathrm{cos}\:\frac{{B}}{\mathrm{4}}−\mathrm{2}{R}\mathrm{sin}\:{C}\mathrm{cos}\:\frac{{B}}{\mathrm{2}}\mathrm{cos}\:\frac{{B}}{\mathrm{4}} \\ $$$$={R}.\mathrm{2sin}\:\frac{\pi−{B}}{\mathrm{2}}\mathrm{cos}\:\frac{{A}−{C}}{\mathrm{2}}\mathrm{cos}\:\frac{{B}}{\mathrm{4}}−\mathrm{2}{R}\mathrm{sin}\:{C}\mathrm{cos}\:\frac{{B}}{\mathrm{2}}\mathrm{cos}\:\frac{{B}}{\mathrm{4}} \\ $$$$={R}.\mathrm{2cos}\:\:\frac{{B}}{\mathrm{2}}\mathrm{cos}\:\frac{{A}−{C}}{\mathrm{2}}\mathrm{cos}\:\frac{{B}}{\mathrm{4}}−\mathrm{2}{R}\mathrm{sin}\:{C}\mathrm{cos}\:\frac{{B}}{\mathrm{2}}\mathrm{cos}\:\frac{{B}}{\mathrm{4}} \\ $$$$=\mathrm{2}{R}\mathrm{cos}\:\frac{{B}}{\mathrm{2}}\mathrm{cos}\:\frac{{B}}{\mathrm{4}}\left\{\mathrm{cos}\:\frac{{A}−{C}}{\mathrm{2}}−\mathrm{sin}\:{C}\right\} \\ $$$$=\mathrm{2}{R}\mathrm{cos}\:\frac{{B}}{\mathrm{2}}\mathrm{cos}\:\frac{{B}}{\mathrm{4}}\left\{\mathrm{cos}\:\frac{{A}−{C}}{\mathrm{2}}−\mathrm{cos}\:\frac{\pi−\mathrm{2}{C}}{\mathrm{2}}\right\} \\ $$$$=\mathrm{2}{R}\mathrm{cos}\:\frac{{B}}{\mathrm{2}}\mathrm{cos}\:\frac{{B}}{\mathrm{4}}.\mathrm{2sin}\:\frac{{A}−{C}+\pi−\mathrm{2}{C}}{\mathrm{2}}\mathrm{sin}\:\frac{\pi−\mathrm{2}{C}−{A}+{C}}{\mathrm{2}} \\ $$$$=\mathrm{2}{R}\mathrm{cos}\:\frac{{B}}{\mathrm{2}}\mathrm{cos}\:\frac{{B}}{\mathrm{4}}.\mathrm{2sin}\:\left(\frac{\pi}{\mathrm{2}}−\frac{{A}−\mathrm{3}{C}}{\mathrm{2}}\right)\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−\frac{{A}+{C}}{\mathrm{2}}\right) \\ $$$$=\mathrm{2}{R}\mathrm{cos}\:\frac{{B}}{\mathrm{2}}\mathrm{cos}\:\frac{{B}}{\mathrm{4}}.\mathrm{2cos}\:\left(\frac{{A}−\mathrm{3}{C}}{\mathrm{2}}\right)\mathrm{cos}\:\:\left(\frac{{A}+{C}}{\mathrm{2}}\right) \\ $$$$=\mathrm{2}{R}\mathrm{cos}\:\frac{{B}}{\mathrm{2}}\mathrm{cos}\:\frac{{B}}{\mathrm{4}}.\mathrm{2cos}\:\left(\frac{{A}−\mathrm{3}{C}}{\mathrm{2}}\right)\mathrm{cos}\:\:\left(\frac{\pi−{B}}{\mathrm{2}}\right) \\ $$$$=\mathrm{2}{R}\mathrm{cos}\:\frac{{B}}{\mathrm{2}}\mathrm{cos}\:\frac{{B}}{\mathrm{4}}.\mathrm{2cos}\:\left(\frac{{A}−\mathrm{3}{C}}{\mathrm{2}}\right)\mathrm{sin}\:\:\frac{{B}}{\mathrm{2}} \\ $$$$={R}\mathrm{sin}\:{B}\mathrm{cos}\:\frac{{B}}{\mathrm{4}}.\mathrm{2cos}\:\left(\frac{{A}−\mathrm{3}{C}}{\mathrm{2}}\right) \\ $$$$={b}.\mathrm{2cos}\:\frac{{B}}{\mathrm{4}}.\mathrm{cos}\:\left(\frac{{A}−\mathrm{3}{C}}{\mathrm{2}}\right) \\ $$$$={b}.\mathrm{2cos}\:\frac{{B}}{\mathrm{4}}.\mathrm{cos}\:\left(\frac{\pi−\left({B}+{C}\right)−\mathrm{3}{C}}{\mathrm{2}}\right) \\ $$$$={b}.\mathrm{2cos}\:\frac{{B}}{\mathrm{4}}.\mathrm{cos}\:\left(\frac{\pi−{B}−\mathrm{4}{C}}{\mathrm{2}}\right) \\ $$$$={b}.\mathrm{2cos}\:\frac{{B}}{\mathrm{4}}.\mathrm{sin}\:\:\left(\frac{{B}+\mathrm{4}{C}}{\mathrm{2}}\right) \\ $$$${Got}\:{stuck}\:{here}. \\ $$$${Either}\:{question}\:{or}\:{my}\:{path}\:{is}\:{wrong}. \\ $$

Commented by peter frank last updated on 14/Sep/19

thank you

$${thank}\:{you} \\ $$$$ \\ $$

Commented by peter frank last updated on 14/Sep/19

thank you

$${thank}\:{you} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com