Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 68191 by peter frank last updated on 06/Sep/19

Answered by mind is power last updated on 06/Sep/19

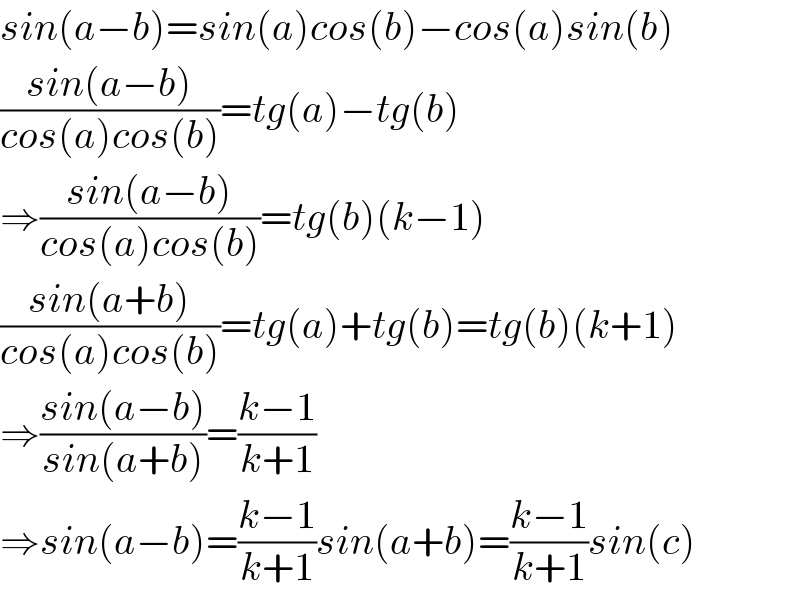
sin(a−b)=sin(a)cos(b)−cos(a)sin(b) ((sin(a−b))/(cos(a)cos(b)))=tg(a)−tg(b) ⇒((sin(a−b))/(cos(a)cos(b)))=tg(b)(k−1) ((sin(a+b))/(cos(a)cos(b)))=tg(a)+tg(b)=tg(b)(k+1) ⇒((sin(a−b))/(sin(a+b)))=((k−1)/(k+1)) ⇒sin(a−b)=((k−1)/(k+1))sin(a+b)=((k−1)/(k+1))sin(c)

$${sin}\left({a}−{b}\right)={sin}\left({a}\right){cos}\left({b}\right)−{cos}\left({a}\right){sin}\left({b}\right) \\ $$$$\frac{{sin}\left({a}−{b}\right)}{{cos}\left({a}\right){cos}\left({b}\right)}={tg}\left({a}\right)−{tg}\left({b}\right) \\ $$$$\Rightarrow\frac{{sin}\left({a}−{b}\right)}{{cos}\left({a}\right){cos}\left({b}\right)}={tg}\left({b}\right)\left({k}−\mathrm{1}\right) \\ $$$$\frac{{sin}\left({a}+{b}\right)}{{cos}\left({a}\right){cos}\left({b}\right)}={tg}\left({a}\right)+{tg}\left({b}\right)={tg}\left({b}\right)\left({k}+\mathrm{1}\right) \\ $$$$\Rightarrow\frac{{sin}\left({a}−{b}\right)}{{sin}\left({a}+{b}\right)}=\frac{{k}−\mathrm{1}}{{k}+\mathrm{1}} \\ $$$$\Rightarrow{sin}\left({a}−{b}\right)=\frac{{k}−\mathrm{1}}{{k}+\mathrm{1}}{sin}\left({a}+{b}\right)=\frac{{k}−\mathrm{1}}{{k}+\mathrm{1}}{sin}\left({c}\right) \\ $$

Commented by peter frank last updated on 07/Sep/19

thank you

$${thank}\:{you} \\ $$

Answered by $@ty@m123 last updated on 06/Sep/19

((tan A)/(tan B))=(k/1) by componendo & dividendo, ((tan A+tan B)/(tan A−tan B)) = ((k+1)/(k−1)) ((((sin A)/(cos A))+((sin B)/(cos B)))/(((sin A)/(cos A))−((sin B)/(cos B)))) = ((k+1)/(k−1)) ((sin Acos B+cos Asin B)/(sin Acos B−cos Asin B)) = ((k+1)/(k−1)) ((sin (A+B))/(sin (A−B ))) = ((k+1)/(k−1)) ((sin C)/(sin (A−B ))) = ((k+1)/(k−1)) I think the question should be: prove that: sin (A−B)=((k−1)/(k+1))sin C

$$\frac{\mathrm{tan}\:{A}}{\mathrm{tan}\:{B}}=\frac{{k}}{\mathrm{1}} \\ $$$${by}\:{componendo}\:\&\:{dividendo}, \\ $$$$\frac{\mathrm{tan}\:{A}+\mathrm{tan}\:{B}}{\mathrm{tan}\:{A}−\mathrm{tan}\:{B}}\:=\:\frac{{k}+\mathrm{1}}{{k}−\mathrm{1}} \\ $$$$\frac{\frac{\mathrm{sin}\:{A}}{\mathrm{cos}\:{A}}+\frac{\mathrm{sin}\:{B}}{\mathrm{cos}\:{B}}}{\frac{\mathrm{sin}\:{A}}{\mathrm{cos}\:{A}}−\frac{\mathrm{sin}\:{B}}{\mathrm{cos}\:{B}}}\:=\:\frac{{k}+\mathrm{1}}{{k}−\mathrm{1}} \\ $$$$\frac{\mathrm{sin}\:{A}\mathrm{cos}\:{B}+\mathrm{cos}\:{A}\mathrm{sin}\:{B}}{\mathrm{sin}\:{A}\mathrm{cos}\:{B}−\mathrm{cos}\:{A}\mathrm{sin}\:{B}}\:=\:\frac{{k}+\mathrm{1}}{{k}−\mathrm{1}} \\ $$$$\frac{\mathrm{sin}\:\left({A}+{B}\right)}{\mathrm{sin}\:\left({A}−{B}\:\right)}\:=\:\frac{{k}+\mathrm{1}}{{k}−\mathrm{1}} \\ $$$$\frac{\mathrm{sin}\:{C}}{\mathrm{sin}\:\left({A}−{B}\:\right)}\:=\:\frac{{k}+\mathrm{1}}{{k}−\mathrm{1}} \\ $$$${I}\:{think}\:{the}\:{question}\:{should}\:{be}: \\ $$$$\:{prove}\:{that}:\:\mathrm{sin}\:\left({A}−{B}\right)=\frac{{k}−\mathrm{1}}{{k}+\mathrm{1}}\mathrm{sin}\:{C} \\ $$

Commented by peter frank last updated on 07/Sep/19

thank you

$${thank}\:{you} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com