
Question Number 68171 by naka3546 last updated on 06/Sep/19
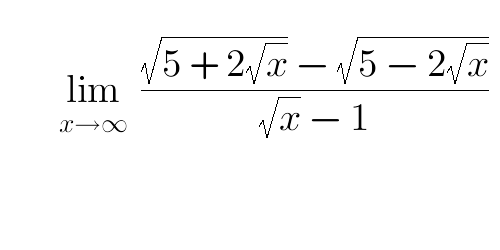
Commented by mathmax by abdo last updated on 06/Sep/19
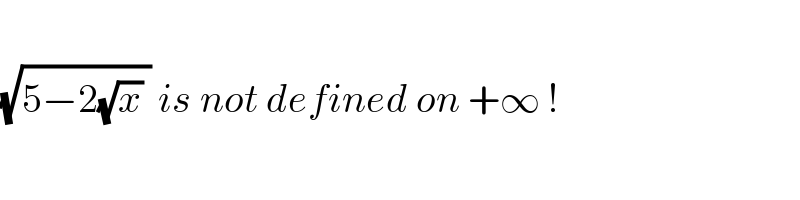
$$ \\ $$$$\sqrt{\mathrm{5}−\mathrm{2}\sqrt{{x}}\:}\:{is}\:{not}\:{defined}\:{on}\:+\infty\:! \\ $$
Commented by mathmax by abdo last updated on 07/Sep/19
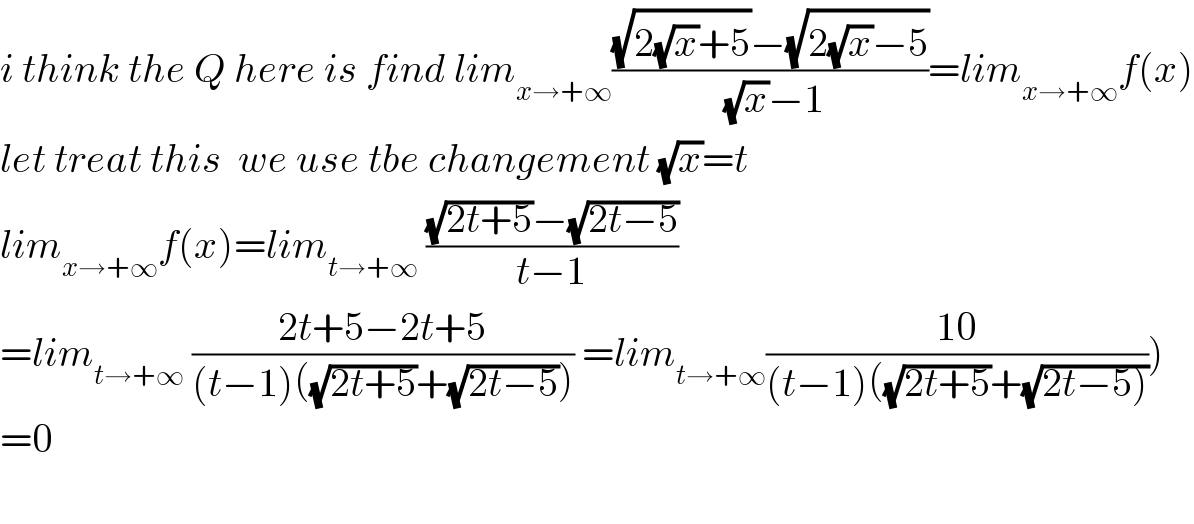
$${i}\:{think}\:{the}\:{Q}\:{here}\:{is}\:{find}\:{lim}_{{x}\rightarrow+\infty} \frac{\sqrt{\mathrm{2}\sqrt{{x}}+\mathrm{5}}−\sqrt{\mathrm{2}\sqrt{{x}}−\mathrm{5}}}{\sqrt{{x}}−\mathrm{1}}={lim}_{{x}\rightarrow+\infty} {f}\left({x}\right) \\ $$$${let}\:{treat}\:{this}\:\:{we}\:{use}\:{tbe}\:{changement}\:\sqrt{{x}}={t}\: \\ $$$${lim}_{{x}\rightarrow+\infty} {f}\left({x}\right)={lim}_{{t}\rightarrow+\infty} \:\frac{\sqrt{\mathrm{2}{t}+\mathrm{5}}−\sqrt{\mathrm{2}{t}−\mathrm{5}}}{{t}−\mathrm{1}} \\ $$$$\left.={lim}_{{t}\rightarrow+\infty} \:\frac{\mathrm{2}{t}+\mathrm{5}−\mathrm{2}{t}+\mathrm{5}}{\left({t}−\mathrm{1}\right)\left(\sqrt{\mathrm{2}{t}+\mathrm{5}}+\sqrt{\mathrm{2}{t}−\mathrm{5}}\right)}\:={lim}_{{t}\rightarrow+\infty} \frac{\mathrm{10}}{\left({t}−\mathrm{1}\right)\left(\sqrt{\mathrm{2}{t}+\mathrm{5}}+\sqrt{\left.\mathrm{2}{t}−\mathrm{5}\right)}\right.}\right) \\ $$$$=\mathrm{0} \\ $$$$ \\ $$
Answered by Kunal12588 last updated on 06/Sep/19

$$\underset{{x}\rightarrow\infty} {{lim}}\frac{\sqrt{\mathrm{5}+\mathrm{2}\sqrt{{x}}}−\sqrt{\mathrm{5}−\mathrm{2}\sqrt{{x}}}}{\sqrt{{x}}−\mathrm{1}} \\ $$$$\sqrt{{x}}={t}\:;\:{x}\rightarrow\infty\:\Rightarrow\:{t}\rightarrow\infty \\ $$$$\underset{{t}\rightarrow\infty} {{lim}}\frac{\sqrt{\mathrm{5}+\mathrm{2}{t}}−\sqrt{\mathrm{5}−\mathrm{2}{t}}}{{t}−\mathrm{1}} \\ $$$$=\underset{{t}\rightarrow\infty} {{lim}}\frac{\sqrt{\frac{\mathrm{5}}{{t}^{\mathrm{2}} }+\frac{\mathrm{2}}{{t}}}−\sqrt{\frac{\mathrm{5}}{{t}^{\mathrm{2}} }−\frac{\mathrm{2}}{{t}}}}{\mathrm{1}−\frac{\mathrm{1}}{{t}}} \\ $$$$=\frac{\mathrm{0}}{\mathrm{1}}=\mathrm{0} \\ $$
