Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

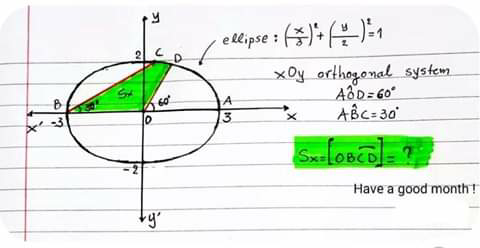
Question Number 68110 by TawaTawa last updated on 05/Sep/19

Commented by kaivan.ahmadi last updated on 07/Sep/19

((y/2))^2 =1−((x/3))^2 ⇒y=±2(√(1−((x/3))^2 )) equation of BC: m=tg30=((√3)/2) y−0=((√3)/2)(x+3)⇒y=((√3)/2)x+((3(√3))/2) equation of OD: m=tg60=(√3) y=(√3)x we find point C ((x/3))^2 +(((√3)/4)x+((3(√3))/4))^2 =1⇒(1/9)x^2 +(3/(16))x^2 +(9/8)x+((27)/(16))=1⇒ 16x^2 +27x^2 +162x+243=144⇒43x^2 +162x+99=0 x_(1,2) =((−162±96)/(86))= { ((((−162+96)/(86))=((−66)/(86))=((−33)/(43)))),((((−162−96)/(86))=−3)) :} so C(((−33)/(43)),((−33(√3))/(86))+((3(√3))/2))=(((−33)/(43)),((96(√3))/(86)))=(((−33)/(43)),((48(√3))/(43))) so this diagram is not true. and now we find point D: ((x/3))^2 +(((√3)/2)x)^2 =1⇒(1/9)x^2 +(3/4)x^2 =1⇒13x^2 =36⇒ x^2 =((36)/(13))⇒x=±(√((36)/(13)))⇒D((√((36)/(13))),(√((108)/(13)))) so we have S_(OBCD) =∫_(−3) ^((−33)/(43)) (((√3)/2)x+((3(√3))/2))dx+∫_((−33)/(43)) ^0 2(√(1−((x/3))^2 ))dx +∫_0 ^(√((36)/(13))) (2(√(1−((x/3))^2 ))−(√3)x)dx

$$\left(\frac{{y}}{\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{1}−\left(\frac{{x}}{\mathrm{3}}\right)^{\mathrm{2}} \Rightarrow{y}=\pm\mathrm{2}\sqrt{\mathrm{1}−\left(\frac{{x}}{\mathrm{3}}\right)^{\mathrm{2}} } \\ $$$${equation}\:{of}\:{BC}: \\ $$$${m}={tg}\mathrm{30}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${y}−\mathrm{0}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\left({x}+\mathrm{3}\right)\Rightarrow{y}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{x}+\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${equation}\:{of}\:{OD}: \\ $$$${m}={tg}\mathrm{60}=\sqrt{\mathrm{3}} \\ $$$${y}=\sqrt{\mathrm{3}}{x} \\ $$$${we}\:{find}\:{point}\:{C} \\ $$$$\left(\frac{{x}}{\mathrm{3}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}{x}+\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{4}}\right)^{\mathrm{2}} =\mathrm{1}\Rightarrow\frac{\mathrm{1}}{\mathrm{9}}{x}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{16}}{x}^{\mathrm{2}} +\frac{\mathrm{9}}{\mathrm{8}}{x}+\frac{\mathrm{27}}{\mathrm{16}}=\mathrm{1}\Rightarrow \\ $$$$\mathrm{16}{x}^{\mathrm{2}} +\mathrm{27}{x}^{\mathrm{2}} +\mathrm{162}{x}+\mathrm{243}=\mathrm{144}\Rightarrow\mathrm{43}{x}^{\mathrm{2}} +\mathrm{162}{x}+\mathrm{99}=\mathrm{0} \\ $$$${x}_{\mathrm{1},\mathrm{2}} =\frac{−\mathrm{162}\pm\mathrm{96}}{\mathrm{86}}=\begin{cases}{\frac{−\mathrm{162}+\mathrm{96}}{\mathrm{86}}=\frac{−\mathrm{66}}{\mathrm{86}}=\frac{−\mathrm{33}}{\mathrm{43}}}\\{\frac{−\mathrm{162}−\mathrm{96}}{\mathrm{86}}=−\mathrm{3}}\end{cases} \\ $$$${so}\:{C}\left(\frac{−\mathrm{33}}{\mathrm{43}},\frac{−\mathrm{33}\sqrt{\mathrm{3}}}{\mathrm{86}}+\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}}\right)=\left(\frac{−\mathrm{33}}{\mathrm{43}},\frac{\mathrm{96}\sqrt{\mathrm{3}}}{\mathrm{86}}\right)=\left(\frac{−\mathrm{33}}{\mathrm{43}},\frac{\mathrm{48}\sqrt{\mathrm{3}}}{\mathrm{43}}\right) \\ $$$${so}\:{this}\:{diagram}\:{is}\:{not}\:{true}. \\ $$$${and}\:{now}\:{we}\:{find}\:{point}\:{D}: \\ $$$$\left(\frac{{x}}{\mathrm{3}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{x}\right)^{\mathrm{2}} =\mathrm{1}\Rightarrow\frac{\mathrm{1}}{\mathrm{9}}{x}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}{x}^{\mathrm{2}} =\mathrm{1}\Rightarrow\mathrm{13}{x}^{\mathrm{2}} =\mathrm{36}\Rightarrow \\ $$$${x}^{\mathrm{2}} =\frac{\mathrm{36}}{\mathrm{13}}\Rightarrow{x}=\pm\sqrt{\frac{\mathrm{36}}{\mathrm{13}}}\Rightarrow{D}\left(\sqrt{\frac{\mathrm{36}}{\mathrm{13}}},\sqrt{\frac{\mathrm{108}}{\mathrm{13}}}\right) \\ $$$${so}\:{we}\:{have} \\ $$$${S}_{{OBCD}} =\int_{−\mathrm{3}} ^{\frac{−\mathrm{33}}{\mathrm{43}}} \left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{x}+\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}}\right){dx}+\int_{\frac{−\mathrm{33}}{\mathrm{43}}} ^{\mathrm{0}} \mathrm{2}\sqrt{\mathrm{1}−\left(\frac{{x}}{\mathrm{3}}\right)^{\mathrm{2}} }{dx} \\ $$$$+\int_{\mathrm{0}} ^{\sqrt{\frac{\mathrm{36}}{\mathrm{13}}}} \:\left(\mathrm{2}\sqrt{\mathrm{1}−\left(\frac{{x}}{\mathrm{3}}\right)^{\mathrm{2}} }−\sqrt{\mathrm{3}}{x}\right){dx} \\ $$$$ \\ $$

Commented by TawaTawa last updated on 08/Sep/19

God bless you sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com