
Question Number 68063 by TawaTawa last updated on 04/Sep/19
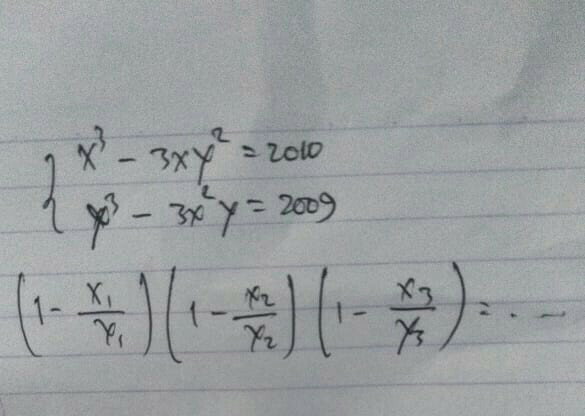
Answered by MJS last updated on 04/Sep/19
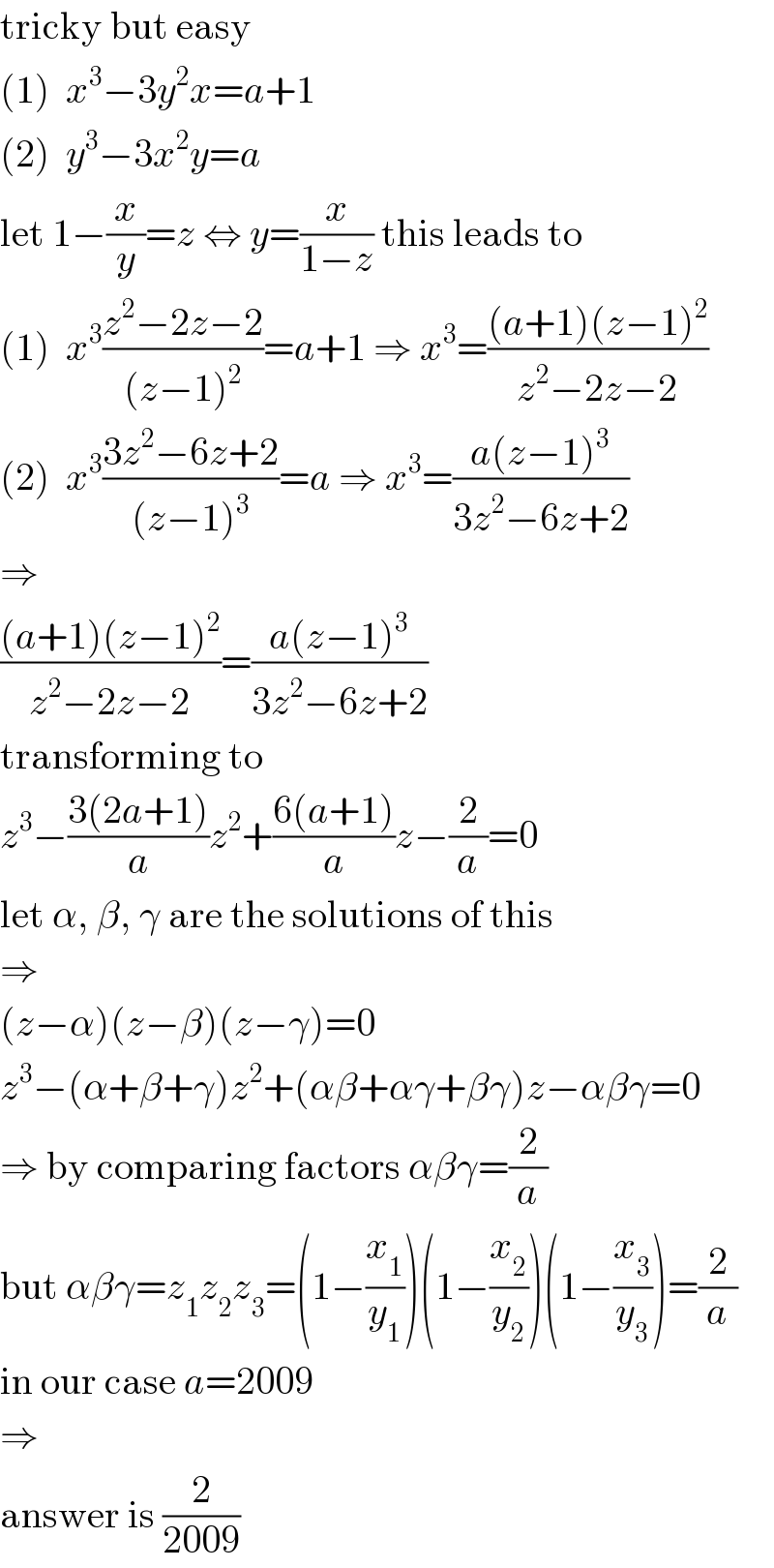
$$\mathrm{tricky}\:\mathrm{but}\:\mathrm{easy} \\ $$$$\left(\mathrm{1}\right)\:\:{x}^{\mathrm{3}} −\mathrm{3}{y}^{\mathrm{2}} {x}={a}+\mathrm{1} \\ $$$$\left(\mathrm{2}\right)\:\:{y}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} {y}={a} \\ $$$$\mathrm{let}\:\mathrm{1}−\frac{{x}}{{y}}={z}\:\Leftrightarrow\:{y}=\frac{{x}}{\mathrm{1}−{z}}\:\mathrm{this}\:\mathrm{leads}\:\mathrm{to} \\ $$$$\left(\mathrm{1}\right)\:\:{x}^{\mathrm{3}} \frac{{z}^{\mathrm{2}} −\mathrm{2}{z}−\mathrm{2}}{\left({z}−\mathrm{1}\right)^{\mathrm{2}} }={a}+\mathrm{1}\:\Rightarrow\:{x}^{\mathrm{3}} =\frac{\left({a}+\mathrm{1}\right)\left({z}−\mathrm{1}\right)^{\mathrm{2}} }{{z}^{\mathrm{2}} −\mathrm{2}{z}−\mathrm{2}} \\ $$$$\left(\mathrm{2}\right)\:\:{x}^{\mathrm{3}} \frac{\mathrm{3}{z}^{\mathrm{2}} −\mathrm{6}{z}+\mathrm{2}}{\left({z}−\mathrm{1}\right)^{\mathrm{3}} }={a}\:\Rightarrow\:{x}^{\mathrm{3}} =\frac{{a}\left({z}−\mathrm{1}\right)^{\mathrm{3}} }{\mathrm{3}{z}^{\mathrm{2}} −\mathrm{6}{z}+\mathrm{2}} \\ $$$$\Rightarrow \\ $$$$\frac{\left({a}+\mathrm{1}\right)\left({z}−\mathrm{1}\right)^{\mathrm{2}} }{{z}^{\mathrm{2}} −\mathrm{2}{z}−\mathrm{2}}=\frac{{a}\left({z}−\mathrm{1}\right)^{\mathrm{3}} }{\mathrm{3}{z}^{\mathrm{2}} −\mathrm{6}{z}+\mathrm{2}} \\ $$$$\mathrm{transforming}\:\mathrm{to} \\ $$$${z}^{\mathrm{3}} −\frac{\mathrm{3}\left(\mathrm{2}{a}+\mathrm{1}\right)}{{a}}{z}^{\mathrm{2}} +\frac{\mathrm{6}\left({a}+\mathrm{1}\right)}{{a}}{z}−\frac{\mathrm{2}}{{a}}=\mathrm{0} \\ $$$$\mathrm{let}\:\alpha,\:\beta,\:\gamma\:\mathrm{are}\:\mathrm{the}\:\mathrm{solutions}\:\mathrm{of}\:\mathrm{this} \\ $$$$\Rightarrow \\ $$$$\left({z}−\alpha\right)\left({z}−\beta\right)\left({z}−\gamma\right)=\mathrm{0} \\ $$$${z}^{\mathrm{3}} −\left(\alpha+\beta+\gamma\right){z}^{\mathrm{2}} +\left(\alpha\beta+\alpha\gamma+\beta\gamma\right){z}−\alpha\beta\gamma=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{by}\:\mathrm{comparing}\:\mathrm{factors}\:\alpha\beta\gamma=\frac{\mathrm{2}}{{a}} \\ $$$$\mathrm{but}\:\alpha\beta\gamma={z}_{\mathrm{1}} {z}_{\mathrm{2}} {z}_{\mathrm{3}} =\left(\mathrm{1}−\frac{{x}_{\mathrm{1}} }{{y}_{\mathrm{1}} }\right)\left(\mathrm{1}−\frac{{x}_{\mathrm{2}} }{{y}_{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{{x}_{\mathrm{3}} }{{y}_{\mathrm{3}} }\right)=\frac{\mathrm{2}}{{a}} \\ $$$$\mathrm{in}\:\mathrm{our}\:\mathrm{case}\:{a}=\mathrm{2009} \\ $$$$\Rightarrow \\ $$$$\mathrm{answer}\:\mathrm{is}\:\frac{\mathrm{2}}{\mathrm{2009}} \\ $$
Commented by TawaTawa last updated on 04/Sep/19
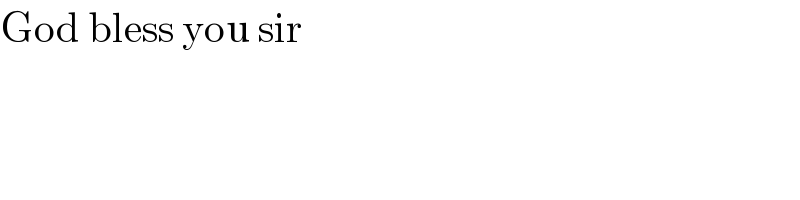
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by Learner-123 last updated on 04/Sep/19

$${Amazing}! \\ $$
