Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 67918 by aliesam last updated on 02/Sep/19

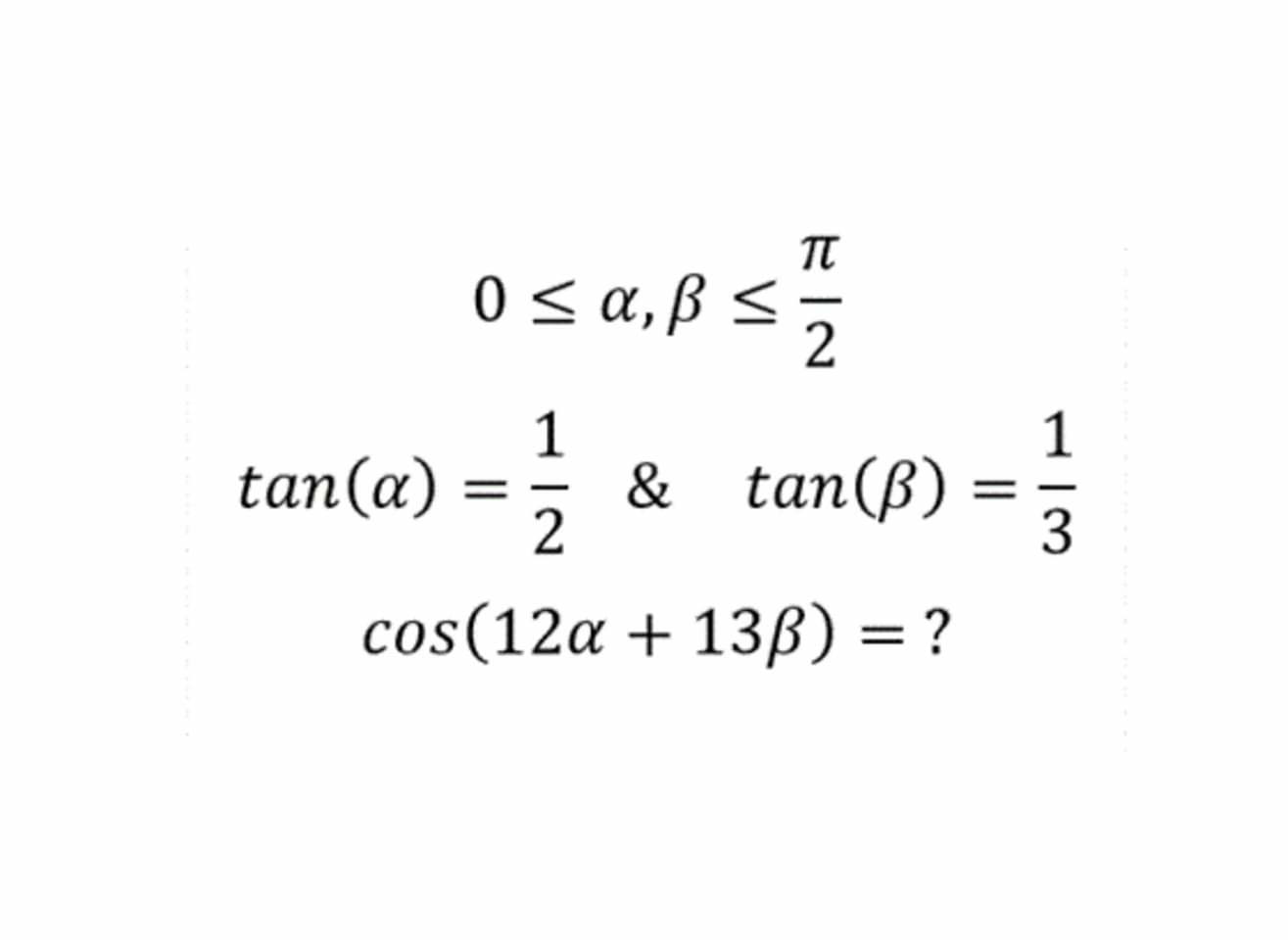
Answered by $@ty@m123 last updated on 02/Sep/19

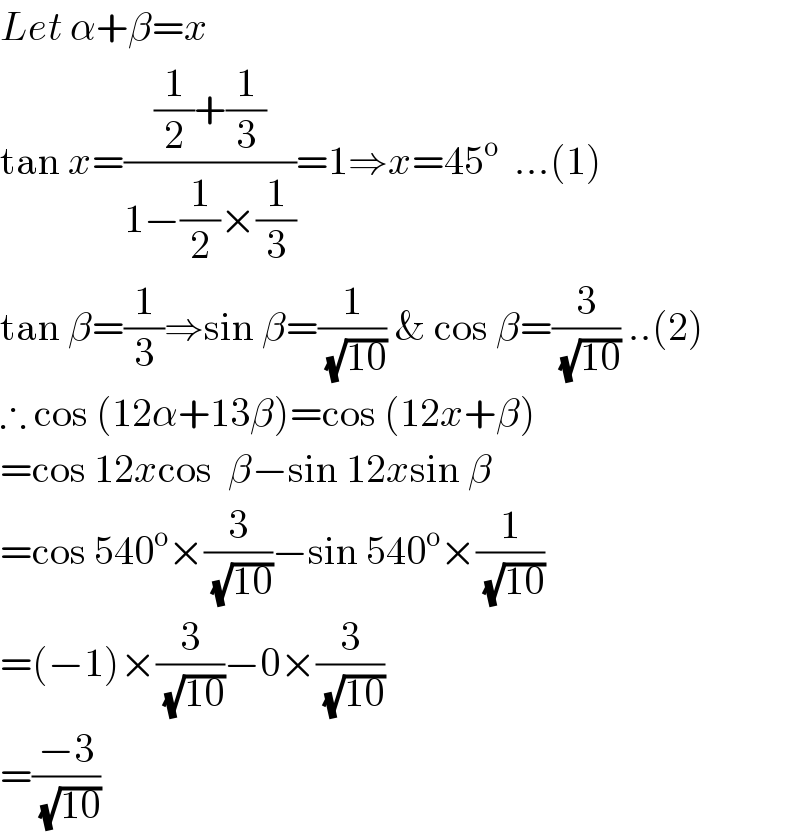
Let α+β=x tan x=(((1/2)+(1/3))/(1−(1/2)×(1/3)))=1⇒x=45^o ...(1) tan β=(1/3)⇒sin β=(1/(√(10))) & cos β=(3/(√(10))) ..(2) ∴ cos (12α+13β)=cos (12x+β) =cos 12xcos β−sin 12xsin β =cos 540^o ×(3/(√(10)))−sin 540^o ×(1/(√(10))) =(−1)×(3/(√(10)))−0×(3/(√(10))) =((−3)/(√(10)))

$${Let}\:\alpha+\beta={x} \\ $$$$\mathrm{tan}\:{x}=\frac{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{3}}}=\mathrm{1}\Rightarrow{x}=\mathrm{45}^{\mathrm{o}} \:\:...\left(\mathrm{1}\right) \\ $$$$\mathrm{tan}\:\beta=\frac{\mathrm{1}}{\mathrm{3}}\Rightarrow\mathrm{sin}\:\beta=\frac{\mathrm{1}}{\sqrt{\mathrm{10}}}\:\&\:\mathrm{cos}\:\beta=\frac{\mathrm{3}}{\sqrt{\mathrm{10}}}\:..\left(\mathrm{2}\right) \\ $$$$\therefore\:\mathrm{cos}\:\left(\mathrm{12}\alpha+\mathrm{13}\beta\right)=\mathrm{cos}\:\left(\mathrm{12}{x}+\beta\right) \\ $$$$=\mathrm{cos}\:\mathrm{12}{x}\mathrm{cos}\:\:\beta−\mathrm{sin}\:\mathrm{12}{x}\mathrm{sin}\:\beta \\ $$$$=\mathrm{cos}\:\mathrm{540}^{\mathrm{o}} ×\frac{\mathrm{3}}{\sqrt{\mathrm{10}}}−\mathrm{sin}\:\mathrm{540}^{\mathrm{o}} ×\frac{\mathrm{1}}{\sqrt{\mathrm{10}}} \\ $$$$=\left(−\mathrm{1}\right)×\frac{\mathrm{3}}{\sqrt{\mathrm{10}}}−\mathrm{0}×\frac{\mathrm{3}}{\sqrt{\mathrm{10}}} \\ $$$$=\frac{−\mathrm{3}}{\sqrt{\mathrm{10}}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com