Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 6762 by 314159 last updated on 24/Jul/16

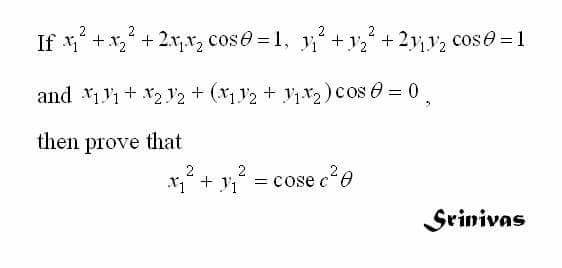
Commented by Yozzii last updated on 24/Jul/16

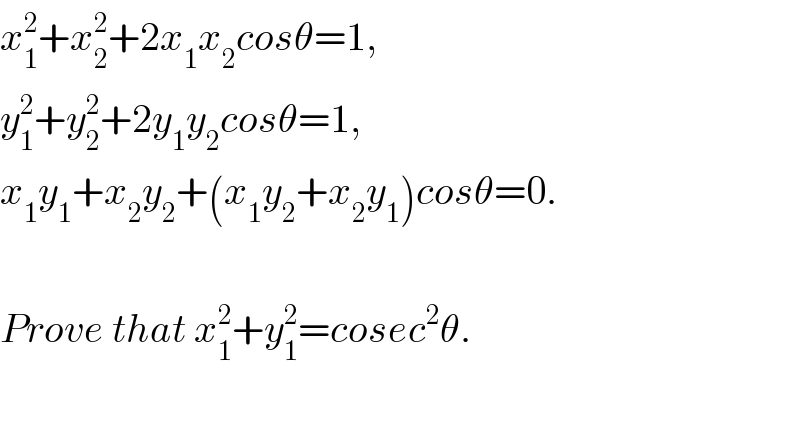
x_1 ^2 +x_2 ^2 +2x_1 x_2 cosθ=1, y_1 ^2 +y_2 ^2 +2y_1 y_2 cosθ=1, x_1 y_1 +x_2 y_2 +(x_1 y_2 +x_2 y_1 )cosθ=0. Prove that x_1 ^2 +y_1 ^2 =cosec^2 θ.

$${x}_{\mathrm{1}} ^{\mathrm{2}} +{x}_{\mathrm{2}} ^{\mathrm{2}} +\mathrm{2}{x}_{\mathrm{1}} {x}_{\mathrm{2}} {cos}\theta=\mathrm{1}, \\ $$$${y}_{\mathrm{1}} ^{\mathrm{2}} +{y}_{\mathrm{2}} ^{\mathrm{2}} +\mathrm{2}{y}_{\mathrm{1}} {y}_{\mathrm{2}} {cos}\theta=\mathrm{1}, \\ $$$${x}_{\mathrm{1}} {y}_{\mathrm{1}} +{x}_{\mathrm{2}} {y}_{\mathrm{2}} +\left({x}_{\mathrm{1}} {y}_{\mathrm{2}} +{x}_{\mathrm{2}} {y}_{\mathrm{1}} \right){cos}\theta=\mathrm{0}. \\ $$$$ \\ $$$${Prove}\:{that}\:{x}_{\mathrm{1}} ^{\mathrm{2}} +{y}_{\mathrm{1}} ^{\mathrm{2}} ={cosec}^{\mathrm{2}} \theta. \\ $$$$ \\ $$

Commented by Yozzii last updated on 24/Jul/16

x_1 ^2 +x_2 ^2 +2x_1 x_2 cosθ=1......................(1) y_1 ^2 +y_2 ^2 +2y_1 y_2 cosθ=1.......................(2) x_1 x_2 +y_1 y_2 +(x_1 y_2 +y_1 x_2 )cosθ=0......(3) or x_1 x_2 +y_1 y_2 =−(x_1 y_2 +y_1 x_2 )cosθ for (3). We start by finding x_2 in terms of x_1 in equation (1). (x_2 +x_1 cosθ)^2 +x_1 ^2 =x_2 ^2 +2x_1 x_2 cosθ+x_1 ^2 +x_1 ^2 cos^2 θ (x_2 +x_1 cosθ)^2 +x_1 ^2 =1+x_1 ^2 cos^2 θ (x_2 +x_1 cosθ)^2 =1−x_1 ^2 sin^2 θ x_2 =−x_1 cosθ±(√(1−x_1 ^2 sin^2 θ)) Similarly, y_2 in terms of y_1 for equation (2) is given by y_2 =−y_1 cosθ±(√(1−y_1 ^2 sin^2 θ)). −−−−−−−−−−−−−−−−−−−−−−−−−−− Working at the second form of equation (3) term by term with x_2 and y_2 substituted leads to the following results. (y_1 x_2 +x_1 y_2 )cosθ=−2x_1 y_1 cos^2 θ±(y_1 (√(1−x_1 ^2 sin^2 θ))+x_1 (√(1−y_1 ^2 sin^2 θ)))cosθ −(y_1 x_2 +x_1 y_2 )cosθ=2x_1 y_1 cos^2 θ∓k {Let k=(y_1 (√(1−x_1 ^2 sin^2 θ))+x_1 (√(1−y_1 ^2 sin^2 θ)))cosθ} and x_2 y_2 =x_1 y_1 cos^2 θ∓{x_1 (√(1−y_1 ^2 sin^2 θ))+y_1 (√(1−x_1 ^2 sin^2 θ))}cosθ+(√((1−x_1 ^2 sin^2 θ)(1−y_1 ^2 sin^2 θ))) x_2 y_2 =x_1 y_1 +x_1 y_1 cos^2 θ∓k+(√((1−x_1 ^2 sin^2 θ)(1−y_1 ^2 sin^2 θ))) ∴ second form of (3) becomes, after cancellation of ∓k from both sides, x_1 y_1 +x_1 y_1 cos^2 θ+(√((1−x_1 ^2 sin^2 θ)(1−y_1 ^2 sin^2 θ)))=2x_1 y_1 cos^2 θ x_1 y_1 (1+cos^2 θ−2cos^2 θ)+(√((1−x_1 ^2 sin^2 θ)(1−y_1 ^2 sin^2 θ)))=0 x_1 y_1 (1−cos^2 θ)+(√((1−x_1 ^2 sin^2 θ)(1−y_1 ^2 sin^2 θ)))=0 x_1 y_1 sin^2 θ=−(√((1−x_1 ^2 sin^2 θ)(1−y_1 ^2 sin^2 θ))) ⇒(1−x_1 ^2 sin^2 θ)(1−y_1 ^2 sin^2 θ)=x_1 ^2 y_1 ^2 sin^4 θ 1−x_1 ^2 sin^2 θ−y_1 ^2 sin^2 θ+x_1 ^2 y_1 ^2 sin^4 θ=x_1 ^2 y_1 ^2 sin^4 θ 1−(x_1 ^2 +y_1 ^2 )sin^2 θ=0 sin^2 θ=(1/(x_1 ^2 +y_1 ^2 ))⇒x_1 ^2 +y_1 ^2 =cosec^2 θ This result assumes that in x_2 and y_2 that both ± signs take the same signs. −−−−−−−−−−−−−−−−−−−−−−−−−−−− Suppose that ± takes different signs between x_2 and y_2 ; i.e x_2 =−x_1 cosθ+(√(1−x_1 ^2 sin^2 θ)) y_2 =−y_1 cosθ−(√(1−y_1 ^2 sin^2 θ)). You can show still that cosec^2 θ=x_1 ^2 +y_1 ^2 . ////

$${x}_{\mathrm{1}} ^{\mathrm{2}} +{x}_{\mathrm{2}} ^{\mathrm{2}} +\mathrm{2}{x}_{\mathrm{1}} {x}_{\mathrm{2}} {cos}\theta=\mathrm{1}......................\left(\mathrm{1}\right) \\ $$$${y}_{\mathrm{1}} ^{\mathrm{2}} +{y}_{\mathrm{2}} ^{\mathrm{2}} +\mathrm{2}{y}_{\mathrm{1}} {y}_{\mathrm{2}} {cos}\theta=\mathrm{1}.......................\left(\mathrm{2}\right) \\ $$$${x}_{\mathrm{1}} {x}_{\mathrm{2}} +{y}_{\mathrm{1}} {y}_{\mathrm{2}} +\left({x}_{\mathrm{1}} {y}_{\mathrm{2}} +{y}_{\mathrm{1}} {x}_{\mathrm{2}} \right){cos}\theta=\mathrm{0}......\left(\mathrm{3}\right) \\ $$$${or}\:{x}_{\mathrm{1}} {x}_{\mathrm{2}} +{y}_{\mathrm{1}} {y}_{\mathrm{2}} =−\left({x}_{\mathrm{1}} {y}_{\mathrm{2}} +{y}_{\mathrm{1}} {x}_{\mathrm{2}} \right){cos}\theta\:\:{for}\:\left(\mathrm{3}\right). \\ $$$$ \\ $$$${We}\:{start}\:{by}\:{finding}\:{x}_{\mathrm{2}} \:{in}\:{terms}\:{of}\:{x}_{\mathrm{1}} \:{in}\:{equation}\:\left(\mathrm{1}\right). \\ $$$$\left({x}_{\mathrm{2}} +{x}_{\mathrm{1}} {cos}\theta\right)^{\mathrm{2}} +{x}_{\mathrm{1}} ^{\mathrm{2}} ={x}_{\mathrm{2}} ^{\mathrm{2}} +\mathrm{2}{x}_{\mathrm{1}} {x}_{\mathrm{2}} {cos}\theta+{x}_{\mathrm{1}} ^{\mathrm{2}} +{x}_{\mathrm{1}} ^{\mathrm{2}} {cos}^{\mathrm{2}} \theta \\ $$$$\left({x}_{\mathrm{2}} +{x}_{\mathrm{1}} {cos}\theta\right)^{\mathrm{2}} +{x}_{\mathrm{1}} ^{\mathrm{2}} =\mathrm{1}+{x}_{\mathrm{1}} ^{\mathrm{2}} {cos}^{\mathrm{2}} \theta \\ $$$$\left({x}_{\mathrm{2}} +{x}_{\mathrm{1}} {cos}\theta\right)^{\mathrm{2}} =\mathrm{1}−{x}_{\mathrm{1}} ^{\mathrm{2}} {sin}^{\mathrm{2}} \theta \\ $$$${x}_{\mathrm{2}} =−{x}_{\mathrm{1}} {cos}\theta\pm\sqrt{\mathrm{1}−{x}_{\mathrm{1}} ^{\mathrm{2}} {sin}^{\mathrm{2}} \theta} \\ $$$$ \\ $$$${Similarly},\:{y}_{\mathrm{2}} \:{in}\:{terms}\:{of}\:{y}_{\mathrm{1}} \:{for}\:{equation}\:\left(\mathrm{2}\right)\:{is}\:{given}\:{by} \\ $$$${y}_{\mathrm{2}} =−{y}_{\mathrm{1}} {cos}\theta\pm\sqrt{\mathrm{1}−{y}_{\mathrm{1}} ^{\mathrm{2}} {sin}^{\mathrm{2}} \theta}. \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$${Working}\:{at}\:{the}\:{second}\:{form}\:{of}\:{equation}\:\left(\mathrm{3}\right)\:{term}\:{by}\:{term} \\ $$$${with}\:{x}_{\mathrm{2}} \:{and}\:{y}_{\mathrm{2}} \:{substituted}\:{leads}\:{to}\:{the}\:{following}\:{results}. \\ $$$$\left({y}_{\mathrm{1}} {x}_{\mathrm{2}} +{x}_{\mathrm{1}} {y}_{\mathrm{2}} \right){cos}\theta=−\mathrm{2}{x}_{\mathrm{1}} {y}_{\mathrm{1}} {cos}^{\mathrm{2}} \theta\pm\left({y}_{\mathrm{1}} \sqrt{\mathrm{1}−{x}_{\mathrm{1}} ^{\mathrm{2}} {sin}^{\mathrm{2}} \theta}+{x}_{\mathrm{1}} \sqrt{\mathrm{1}−{y}_{\mathrm{1}} ^{\mathrm{2}} {sin}^{\mathrm{2}} \theta}\right){cos}\theta \\ $$$$−\left({y}_{\mathrm{1}} {x}_{\mathrm{2}} +{x}_{\mathrm{1}} {y}_{\mathrm{2}} \right){cos}\theta=\mathrm{2}{x}_{\mathrm{1}} {y}_{\mathrm{1}} {cos}^{\mathrm{2}} \theta\mp{k}\:\:\:\left\{{Let}\:{k}=\left({y}_{\mathrm{1}} \sqrt{\mathrm{1}−{x}_{\mathrm{1}} ^{\mathrm{2}} {sin}^{\mathrm{2}} \theta}+{x}_{\mathrm{1}} \sqrt{\mathrm{1}−{y}_{\mathrm{1}} ^{\mathrm{2}} {sin}^{\mathrm{2}} \theta}\right){cos}\theta\right\} \\ $$$${and} \\ $$$${x}_{\mathrm{2}} {y}_{\mathrm{2}} ={x}_{\mathrm{1}} {y}_{\mathrm{1}} {cos}^{\mathrm{2}} \theta\mp\left\{{x}_{\mathrm{1}} \sqrt{\mathrm{1}−{y}_{\mathrm{1}} ^{\mathrm{2}} {sin}^{\mathrm{2}} \theta}+{y}_{\mathrm{1}} \sqrt{\mathrm{1}−{x}_{\mathrm{1}} ^{\mathrm{2}} {sin}^{\mathrm{2}} \theta}\right\}{cos}\theta+\sqrt{\left(\mathrm{1}−{x}_{\mathrm{1}} ^{\mathrm{2}} {sin}^{\mathrm{2}} \theta\right)\left(\mathrm{1}−{y}_{\mathrm{1}} ^{\mathrm{2}} {sin}^{\mathrm{2}} \theta\right)} \\ $$$${x}_{\mathrm{2}} {y}_{\mathrm{2}} ={x}_{\mathrm{1}} {y}_{\mathrm{1}} +{x}_{\mathrm{1}} {y}_{\mathrm{1}} {cos}^{\mathrm{2}} \theta\mp{k}+\sqrt{\left(\mathrm{1}−{x}_{\mathrm{1}} ^{\mathrm{2}} {sin}^{\mathrm{2}} \theta\right)\left(\mathrm{1}−{y}_{\mathrm{1}} ^{\mathrm{2}} {sin}^{\mathrm{2}} \theta\right)} \\ $$$$ \\ $$$$\therefore\:{second}\:{form}\:{of}\:\left(\mathrm{3}\right)\:{becomes},\:{after}\:{cancellation}\:{of}\:\mp{k}\:{from}\:{both}\:{sides}, \\ $$$${x}_{\mathrm{1}} {y}_{\mathrm{1}} +{x}_{\mathrm{1}} {y}_{\mathrm{1}} {cos}^{\mathrm{2}} \theta+\sqrt{\left(\mathrm{1}−{x}_{\mathrm{1}} ^{\mathrm{2}} {sin}^{\mathrm{2}} \theta\right)\left(\mathrm{1}−{y}_{\mathrm{1}} ^{\mathrm{2}} {sin}^{\mathrm{2}} \theta\right)}=\mathrm{2}{x}_{\mathrm{1}} {y}_{\mathrm{1}} {cos}^{\mathrm{2}} \theta \\ $$$${x}_{\mathrm{1}} {y}_{\mathrm{1}} \left(\mathrm{1}+{cos}^{\mathrm{2}} \theta−\mathrm{2}{cos}^{\mathrm{2}} \theta\right)+\sqrt{\left(\mathrm{1}−{x}_{\mathrm{1}} ^{\mathrm{2}} {sin}^{\mathrm{2}} \theta\right)\left(\mathrm{1}−{y}_{\mathrm{1}} ^{\mathrm{2}} {sin}^{\mathrm{2}} \theta\right)}=\mathrm{0} \\ $$$${x}_{\mathrm{1}} {y}_{\mathrm{1}} \left(\mathrm{1}−{cos}^{\mathrm{2}} \theta\right)+\sqrt{\left(\mathrm{1}−{x}_{\mathrm{1}} ^{\mathrm{2}} {sin}^{\mathrm{2}} \theta\right)\left(\mathrm{1}−{y}_{\mathrm{1}} ^{\mathrm{2}} {sin}^{\mathrm{2}} \theta\right)}=\mathrm{0} \\ $$$${x}_{\mathrm{1}} {y}_{\mathrm{1}} {sin}^{\mathrm{2}} \theta=−\sqrt{\left(\mathrm{1}−{x}_{\mathrm{1}} ^{\mathrm{2}} {sin}^{\mathrm{2}} \theta\right)\left(\mathrm{1}−{y}_{\mathrm{1}} ^{\mathrm{2}} {sin}^{\mathrm{2}} \theta\right)} \\ $$$$\Rightarrow\left(\mathrm{1}−{x}_{\mathrm{1}} ^{\mathrm{2}} {sin}^{\mathrm{2}} \theta\right)\left(\mathrm{1}−{y}_{\mathrm{1}} ^{\mathrm{2}} {sin}^{\mathrm{2}} \theta\right)={x}_{\mathrm{1}} ^{\mathrm{2}} {y}_{\mathrm{1}} ^{\mathrm{2}} {sin}^{\mathrm{4}} \theta \\ $$$$\mathrm{1}−{x}_{\mathrm{1}} ^{\mathrm{2}} {sin}^{\mathrm{2}} \theta−{y}_{\mathrm{1}} ^{\mathrm{2}} {sin}^{\mathrm{2}} \theta+{x}_{\mathrm{1}} ^{\mathrm{2}} {y}_{\mathrm{1}} ^{\mathrm{2}} {sin}^{\mathrm{4}} \theta={x}_{\mathrm{1}} ^{\mathrm{2}} {y}_{\mathrm{1}} ^{\mathrm{2}} {sin}^{\mathrm{4}} \theta \\ $$$$\mathrm{1}−\left({x}_{\mathrm{1}} ^{\mathrm{2}} +{y}_{\mathrm{1}} ^{\mathrm{2}} \right){sin}^{\mathrm{2}} \theta=\mathrm{0} \\ $$$${sin}^{\mathrm{2}} \theta=\frac{\mathrm{1}}{{x}_{\mathrm{1}} ^{\mathrm{2}} +{y}_{\mathrm{1}} ^{\mathrm{2}} }\Rightarrow{x}_{\mathrm{1}} ^{\mathrm{2}} +{y}_{\mathrm{1}} ^{\mathrm{2}} ={cosec}^{\mathrm{2}} \theta\:\:\:\:\:\:\:\:\: \\ $$$${This}\:{result}\:{assumes}\:{that}\:{in}\:{x}_{\mathrm{2}} \:{and}\:{y}_{\mathrm{2}} \\ $$$${that}\:{both}\:\pm\:{signs}\:{take}\:{the}\:{same}\:{signs}. \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$${Suppose}\:{that}\:\pm\:{takes}\:{different}\:{signs} \\ $$$${between}\:{x}_{\mathrm{2}} \:{and}\:{y}_{\mathrm{2}} ;\:{i}.{e} \\ $$$${x}_{\mathrm{2}} =−{x}_{\mathrm{1}} {cos}\theta+\sqrt{\mathrm{1}−{x}_{\mathrm{1}} ^{\mathrm{2}} {sin}^{\mathrm{2}} \theta} \\ $$$${y}_{\mathrm{2}} =−{y}_{\mathrm{1}} {cos}\theta−\sqrt{\mathrm{1}−{y}_{\mathrm{1}} ^{\mathrm{2}} {sin}^{\mathrm{2}} \theta}. \\ $$$${You}\:{can}\:{show}\:{still}\:{that}\:{cosec}^{\mathrm{2}} \theta={x}_{\mathrm{1}} ^{\mathrm{2}} +{y}_{\mathrm{1}} ^{\mathrm{2}} .\:\:\:\://// \\ $$

Answered by Yozzii last updated on 24/Jul/16

Check comments for a solution I shared.

$${Check}\:{comments}\:{for}\:{a}\:{solution}\:{I}\:{shared}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com