
Question Number 67561 by azizullah last updated on 28/Aug/19
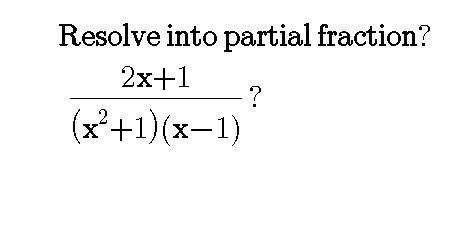
Answered by Rasheed.Sindhi last updated on 28/Aug/19

$${Let}\:\frac{\mathrm{2}{x}+\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}−\mathrm{1}\right)}=\frac{{Ax}+{B}}{{x}^{\mathrm{2}} +\mathrm{1}}+\frac{{C}}{{x}−\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\left({Ax}+{B}\right)\left({x}−\mathrm{1}\right)+{C}\left({x}^{\mathrm{2}} +\mathrm{1}\right)=\mathrm{2}{x}+\mathrm{1} \\ $$$${x}=\mathrm{1}\Rightarrow\mathrm{2}{C}=\mathrm{3}\Rightarrow{C}=\mathrm{3}/\mathrm{2} \\ $$$${Ax}^{\mathrm{2}} +{Bx}−{Ax}−{B}+{Cx}^{\mathrm{2}} +{C}=\mathrm{2}{x}+\mathrm{1} \\ $$$$\left({A}+{C}\right){x}^{\mathrm{2}} +\left({B}−{A}\right){x}+{C}−{B}=\mathrm{0}{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1} \\ $$$$\:\:\:\:{A}+{C}=\mathrm{0}\Rightarrow{A}=−{C}=−\mathrm{3}/\mathrm{2} \\ $$$$\:\:\:\:{B}−{A}=\mathrm{2}\Rightarrow{B}={A}+\mathrm{2}=−\mathrm{3}/\mathrm{2}\:+\mathrm{2}=\mathrm{1}/\mathrm{2} \\ $$$$\:\:\:\:{C}−{B}=\mathrm{1}\Rightarrow\mathrm{3}/\mathrm{2}−\mathrm{1}/\mathrm{2}=\mathrm{1} \\ $$$$ \\ $$$$\:\frac{\mathrm{2}{x}+\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}−\mathrm{1}\right)}=\frac{−\frac{\mathrm{3}}{\mathrm{2}}{x}+\frac{\mathrm{1}}{\mathrm{2}}}{{x}^{\mathrm{2}} +\mathrm{1}}+\frac{\frac{\mathrm{3}}{\mathrm{2}}}{{x}−\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{−\mathrm{3}{x}+\mathrm{1}}{\mathrm{2}\left({x}^{\mathrm{2}} +\mathrm{1}\right)}+\frac{\mathrm{3}}{\mathrm{2}\left({x}−\mathrm{1}\right)} \\ $$$$ \\ $$
Commented by azizullah last updated on 29/Aug/19

$$\:\:\:\:\:\:\:\boldsymbol{\mathrm{Sir}}\:\boldsymbol{\mathrm{Alot}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{thanks}}! \\ $$
Commented by Rasheed.Sindhi last updated on 30/Aug/19
You're welcome mr Azizullah!
