
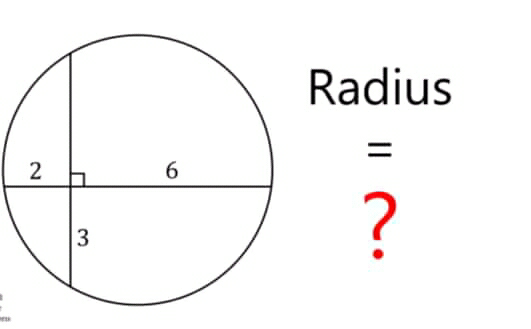
Question Number 67254 by TawaTawa last updated on 24/Aug/19
Commented by Rasheed.Sindhi last updated on 24/Aug/19

$$\:\:\:\:\:{Analytical}\:{Method} \\ $$$${x}-{axis}:{Horizanal}\:{Chord} \\ $$$${y}-{axis}:{Vertical}\:{Chord} \\ $$$${Three}\:{points}\:{on}\:{the}\:{circle}: \\ $$$$\:{A}\left(\mathrm{6},\mathrm{0}\right),{B}\left(−\mathrm{2},\mathrm{0}\right)\:\&\:{C}\left(\mathrm{0},−\mathrm{3}\right) \\ $$$${Find}\:{out}\:{circumcentre}\:{O}\left({x},{y}\right)\:{of}\:\bigtriangleup{ABC}\: \\ $$$${Radius}=\mid{OA}\mid\:{or}\:\mid{OB}\mid\:{or}\:\mid{OC}\mid \\ $$$$ \\ $$
Commented by MJS last updated on 24/Aug/19
![Sir Rasheed′s idea completed a=8 b=(√(2^2 +3^2 ))=(√(13)) c=(√(3^2 +6^2 ))=(√(45)) δ=(√((a+b+c)(−a+b+c)(a−b+c)(a+b−c))) R=((abc)/δ)=((√(65))/2) [Heron′s formula; search the web for it]](Q67268.png)
$$\mathrm{Sir}\:\mathrm{Rasheed}'\mathrm{s}\:\mathrm{idea}\:\mathrm{completed} \\ $$$${a}=\mathrm{8}\:{b}=\sqrt{\mathrm{2}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} }=\sqrt{\mathrm{13}}\:\:{c}=\sqrt{\mathrm{3}^{\mathrm{2}} +\mathrm{6}^{\mathrm{2}} }=\sqrt{\mathrm{45}} \\ $$$$\delta=\sqrt{\left({a}+{b}+{c}\right)\left(−{a}+{b}+{c}\right)\left({a}−{b}+{c}\right)\left({a}+{b}−{c}\right)} \\ $$$${R}=\frac{{abc}}{\delta}=\frac{\sqrt{\mathrm{65}}}{\mathrm{2}}\:\left[\mathrm{Heron}'\mathrm{s}\:\mathrm{formula};\:\mathrm{search}\:\mathrm{the}\:\mathrm{web}\:\mathrm{for}\:\mathrm{it}\right] \\ $$
Commented by TawaTawa last updated on 25/Aug/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sirs}.\: \\ $$
Commented by TawaTawa last updated on 25/Aug/19
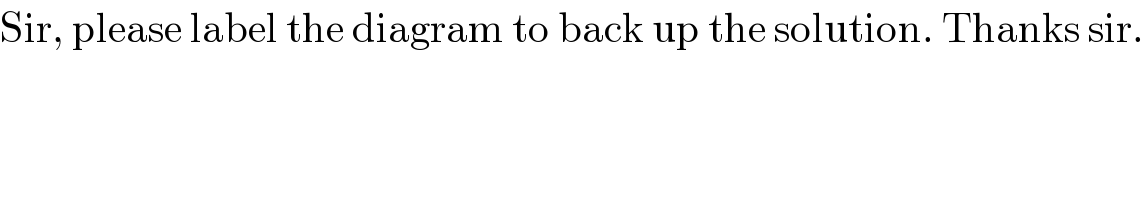
$$\mathrm{Sir},\:\mathrm{please}\:\mathrm{label}\:\mathrm{the}\:\mathrm{diagram}\:\mathrm{to}\:\mathrm{back}\:\mathrm{up}\:\mathrm{the}\:\mathrm{solution}.\:\mathrm{Thanks}\:\mathrm{sir}. \\ $$
Commented by Rasheed.Sindhi last updated on 25/Aug/19

$$\mathcal{T}^{\mathcal{H}^{\mathcal{A}} \mathcal{N}} \mathcal{K}{s}\:\mathcal{S}\imath{r}\:\mathrm{MJS}! \\ $$
Commented by TawaTawa last updated on 25/Aug/19
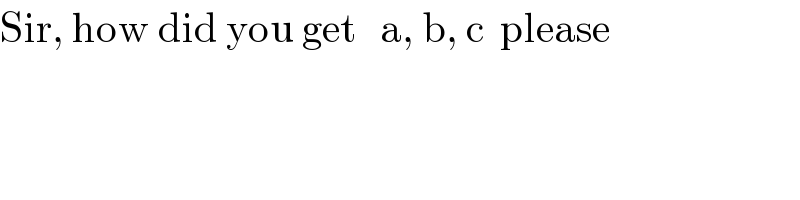
$$\mathrm{Sir},\:\mathrm{how}\:\mathrm{did}\:\mathrm{you}\:\mathrm{get}\:\:\:\mathrm{a},\:\mathrm{b},\:\mathrm{c}\:\:\mathrm{please} \\ $$
Commented by Tony Lin last updated on 25/Aug/19
Commented by Tony Lin last updated on 25/Aug/19
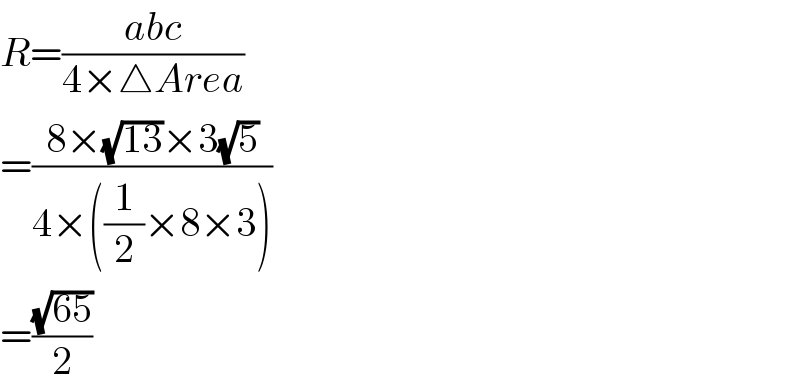
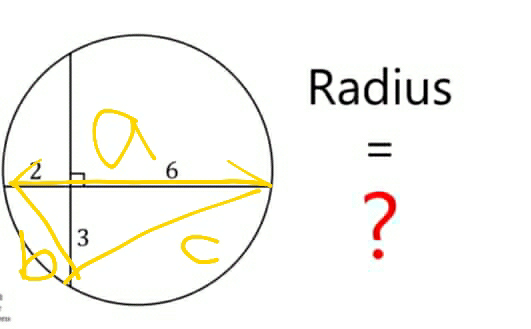
$${R}=\frac{{abc}}{\mathrm{4}×\bigtriangleup{Area}} \\ $$$$=\frac{\mathrm{8}×\sqrt{\mathrm{13}}×\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{4}×\left(\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{8}×\mathrm{3}\right)} \\ $$$$=\frac{\sqrt{\mathrm{65}}}{\mathrm{2}} \\ $$
Commented by Tony Lin last updated on 25/Aug/19
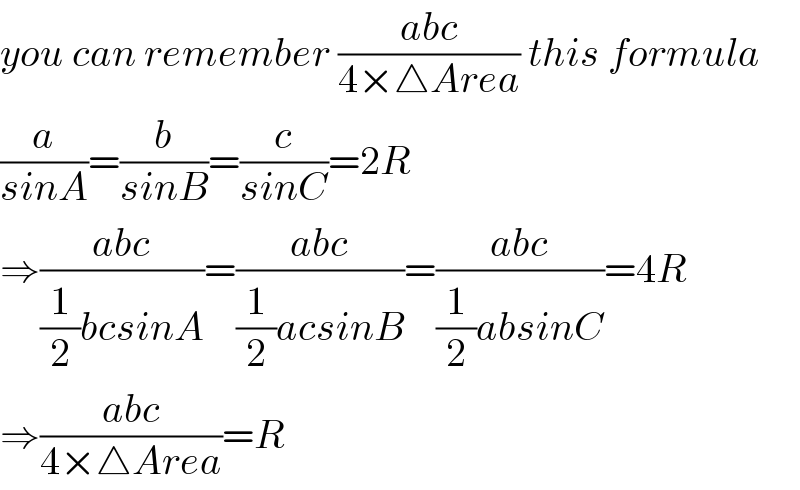
$${you}\:{can}\:{remember}\:\frac{{abc}}{\mathrm{4}×\bigtriangleup{Area}}\:{this}\:{formula} \\ $$$$\frac{{a}}{{sinA}}=\frac{{b}}{{sinB}}=\frac{{c}}{{sinC}}=\mathrm{2}{R} \\ $$$$\Rightarrow\frac{{abc}}{\frac{\mathrm{1}}{\mathrm{2}}{bcsinA}}=\frac{{abc}}{\frac{\mathrm{1}}{\mathrm{2}}{acsinB}}=\frac{{abc}}{\frac{\mathrm{1}}{\mathrm{2}}{absinC}}=\mathrm{4}{R} \\ $$$$\Rightarrow\frac{{abc}}{\mathrm{4}×\bigtriangleup{Area}}={R} \\ $$
Commented by TawaTawa last updated on 25/Aug/19
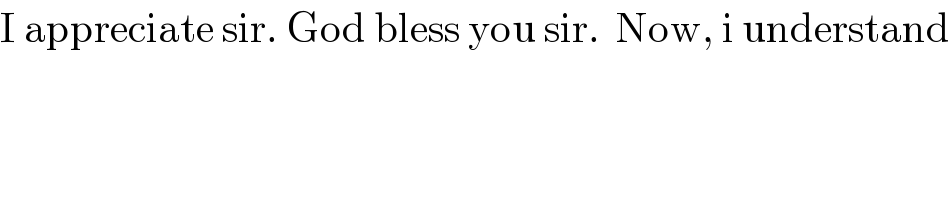
$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\:\mathrm{Now},\:\mathrm{i}\:\mathrm{understand} \\ $$
Answered by mr W last updated on 24/Aug/19
Commented by mr W last updated on 24/Aug/19
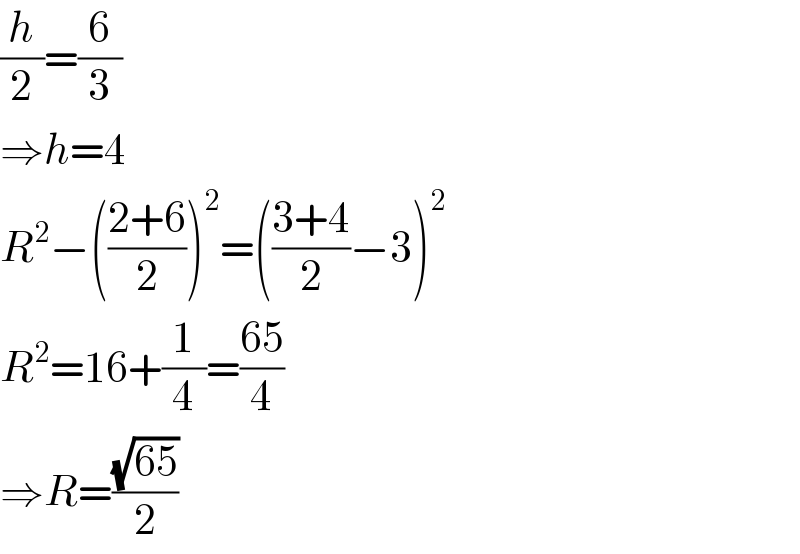
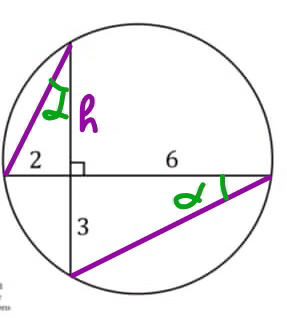
$$\frac{{h}}{\mathrm{2}}=\frac{\mathrm{6}}{\mathrm{3}} \\ $$$$\Rightarrow{h}=\mathrm{4} \\ $$$${R}^{\mathrm{2}} −\left(\frac{\mathrm{2}+\mathrm{6}}{\mathrm{2}}\right)^{\mathrm{2}} =\left(\frac{\mathrm{3}+\mathrm{4}}{\mathrm{2}}−\mathrm{3}\right)^{\mathrm{2}} \\ $$$${R}^{\mathrm{2}} =\mathrm{16}+\frac{\mathrm{1}}{\mathrm{4}}=\frac{\mathrm{65}}{\mathrm{4}} \\ $$$$\Rightarrow{R}=\frac{\sqrt{\mathrm{65}}}{\mathrm{2}} \\ $$
Commented by TawaTawa last updated on 25/Aug/19
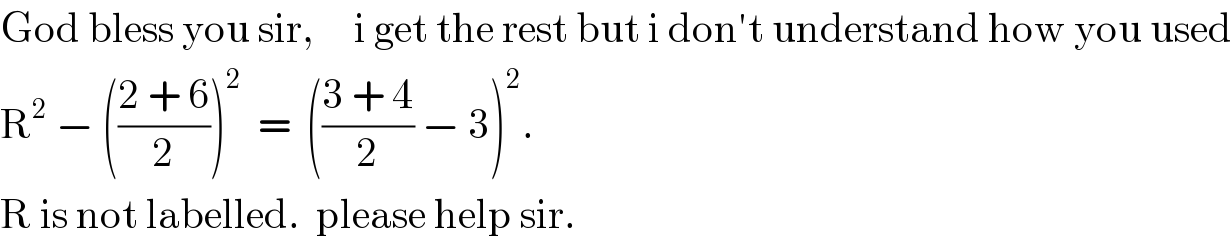
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir},\:\:\:\:\:\mathrm{i}\:\mathrm{get}\:\mathrm{the}\:\mathrm{rest}\:\mathrm{but}\:\mathrm{i}\:\mathrm{don}'\mathrm{t}\:\mathrm{understand}\:\mathrm{how}\:\mathrm{you}\:\mathrm{used} \\ $$$$\mathrm{R}^{\mathrm{2}} \:−\:\left(\frac{\mathrm{2}\:+\:\mathrm{6}}{\mathrm{2}}\right)^{\mathrm{2}} \:\:=\:\:\left(\frac{\mathrm{3}\:+\:\mathrm{4}}{\mathrm{2}}\:−\:\mathrm{3}\right)^{\mathrm{2}} . \\ $$$$\mathrm{R}\:\mathrm{is}\:\mathrm{not}\:\mathrm{labelled}.\:\:\mathrm{please}\:\mathrm{help}\:\mathrm{sir}. \\ $$
Commented by mr W last updated on 25/Aug/19
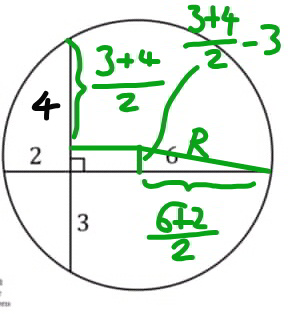
Commented by TawaTawa last updated on 25/Aug/19

$$\mathrm{Sir},\:\mathrm{please}\:\mathrm{give}\:\mathrm{me}\:\mathrm{any}\:\mathrm{question}\:\mathrm{on}\:\mathrm{finding}\:\mathrm{area}\:\mathrm{of}\:\mathrm{shaded}\:\mathrm{portion}\:\mathrm{i}\:\mathrm{should} \\ $$$$\mathrm{try}.\:\mathrm{Thanks}\:\mathrm{sir}. \\ $$
Commented by TawaTawa last updated on 25/Aug/19
$$\mathrm{Wow},\:\:\mathrm{i}\:\mathrm{understand}\:\mathrm{it}\:\mathrm{now}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
