
Question Number 67215 by Learner-123 last updated on 24/Aug/19

Commented by Learner-123 last updated on 24/Aug/19
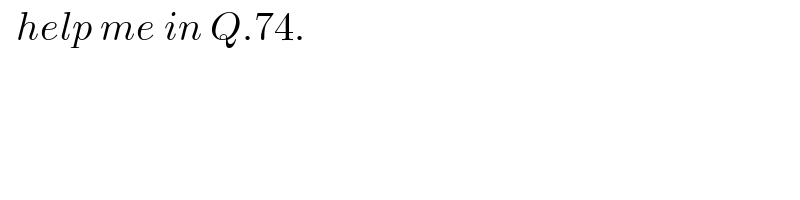
$$\:\:{help}\:{me}\:{in}\:{Q}.\mathrm{74}. \\ $$
Answered by mr W last updated on 24/Aug/19

$${h}=\mathrm{4}{m} \\ $$$${s}_{\mathrm{1}} ={h}+\mathrm{0}.\mathrm{75}{h}=\mathrm{1}.\mathrm{75}{h} \\ $$$${s}_{\mathrm{2}} =\mathrm{0}.\mathrm{75}{h}+\mathrm{0}.\mathrm{75}^{\mathrm{2}} {h}=\mathrm{0}.\mathrm{75}×\mathrm{1}.\mathrm{75}{h} \\ $$$$.... \\ $$$${s}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{s}_{{n}} =\frac{\mathrm{1}.\mathrm{75}{h}}{\mathrm{1}−\mathrm{0}.\mathrm{75}}=\mathrm{7}{h}=\mathrm{7}×\mathrm{4}=\mathrm{28}{m} \\ $$$$ \\ $$$${t}_{\mathrm{1}} =\sqrt{\frac{{h}}{\mathrm{4}.\mathrm{9}}}+\sqrt{\frac{\mathrm{0}.\mathrm{75}{h}}{\mathrm{4}.\mathrm{9}}}=\left(\mathrm{1}+\sqrt{\mathrm{0}.\mathrm{75}}\right)\sqrt{\frac{{h}}{\mathrm{4}.\mathrm{9}}} \\ $$$${t}_{\mathrm{2}} =\sqrt{\frac{\mathrm{0}.\mathrm{75}{h}}{\mathrm{4}.\mathrm{9}}}+\sqrt{\frac{\mathrm{0}.\mathrm{75}^{\mathrm{2}} {h}}{\mathrm{4}.\mathrm{9}}}=\sqrt{\mathrm{0}.\mathrm{75}}\left(\mathrm{1}+\sqrt{\mathrm{0}.\mathrm{75}}\right)\sqrt{\frac{{h}}{\mathrm{4}.\mathrm{9}}} \\ $$$$... \\ $$$${t}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{t}_{{n}} =\frac{\mathrm{1}+\sqrt{\mathrm{0}.\mathrm{75}}}{\mathrm{1}−\sqrt{\mathrm{0}.\mathrm{75}}}×\sqrt{\frac{{h}}{\mathrm{4}.\mathrm{9}}}=\mathrm{12}.\mathrm{58}\:{sec} \\ $$
Commented by Learner-123 last updated on 24/Aug/19

$${thanks}\:{sir}. \\ $$
