Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 66602 by aliesam last updated on 17/Aug/19

Commented by Rio Michael last updated on 17/Aug/19

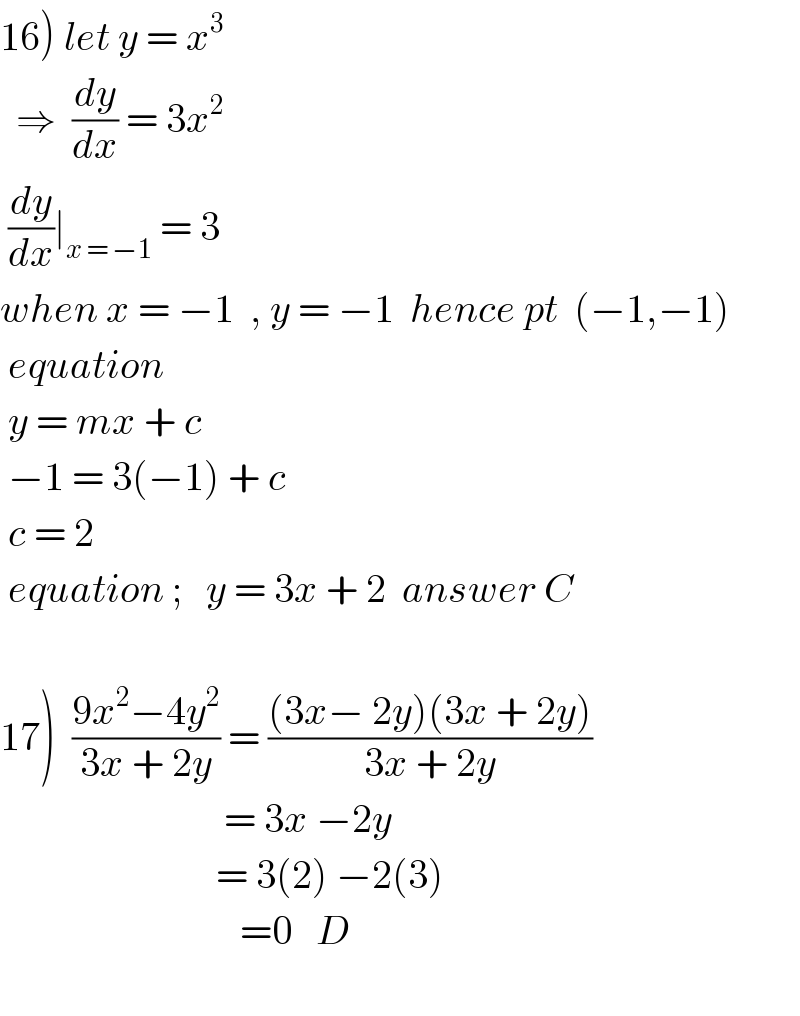
16) let y = x^3 ⇒ (dy/dx) = 3x^2 (dy/dx)∣_(x = −1) = 3 when x = −1 , y = −1 hence pt (−1,−1) equation y = mx + c −1 = 3(−1) + c c = 2 equation ; y = 3x + 2 answer C 17) ((9x^2 −4y^2 )/(3x + 2y)) = (((3x− 2y)(3x + 2y))/(3x + 2y)) = 3x −2y = 3(2) −2(3) =0 D

$$\left.\mathrm{16}\right)\:{let}\:{y}\:=\:{x}^{\mathrm{3}} \\ $$$$\:\:\Rightarrow\:\:\frac{{dy}}{{dx}}\:=\:\mathrm{3}{x}^{\mathrm{2}} \\ $$$$\:\frac{{dy}}{{dx}}\mid_{{x}\:=\:−\mathrm{1}} \:=\:\mathrm{3} \\ $$$${when}\:{x}\:=\:−\mathrm{1}\:\:,\:{y}\:=\:−\mathrm{1}\:\:{hence}\:{pt}\:\:\left(−\mathrm{1},−\mathrm{1}\right) \\ $$$$\:{equation} \\ $$$$\:{y}\:=\:{mx}\:+\:{c} \\ $$$$\:−\mathrm{1}\:=\:\mathrm{3}\left(−\mathrm{1}\right)\:+\:{c} \\ $$$$\:{c}\:=\:\mathrm{2} \\ $$$$\:{equation}\:;\:\:\:{y}\:=\:\mathrm{3}{x}\:+\:\mathrm{2}\:\:{answer}\:{C} \\ $$$$ \\ $$$$\left.\mathrm{17}\right)\:\:\frac{\mathrm{9}{x}^{\mathrm{2}} −\mathrm{4}{y}^{\mathrm{2}} }{\mathrm{3}{x}\:+\:\mathrm{2}{y}}\:=\:\frac{\left(\mathrm{3}{x}−\:\mathrm{2}{y}\right)\left(\mathrm{3}{x}\:+\:\mathrm{2}{y}\right)}{\mathrm{3}{x}\:+\:\mathrm{2}{y}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{3}{x}\:−\mathrm{2}{y} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{3}\left(\mathrm{2}\right)\:−\mathrm{2}\left(\mathrm{3}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{0}\:\:\:{D} \\ $$$$ \\ $$

Commented by aliesam last updated on 17/Aug/19

perfect

$${perfect} \\ $$

Commented by mathmax by abdo last updated on 17/Aug/19

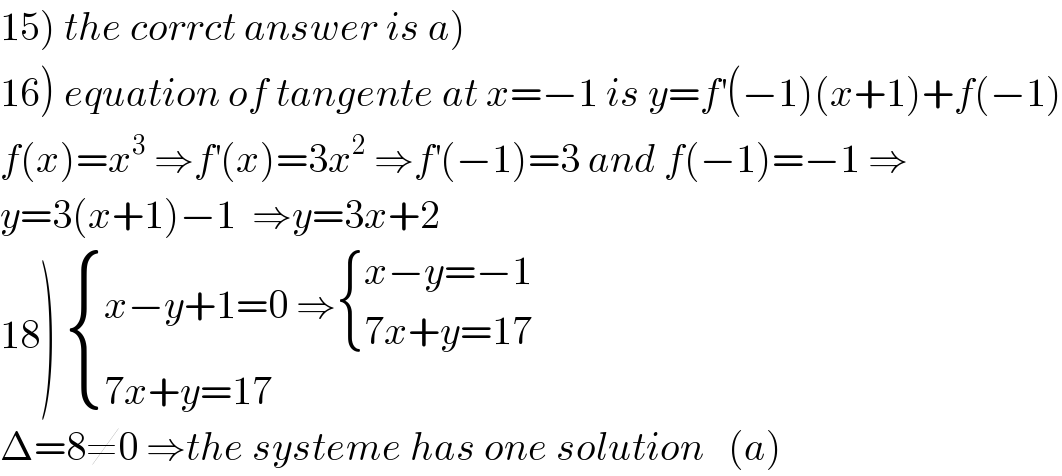
15) the corrct answer is a) 16) equation of tangente at x=−1 is y=f^′ (−1)(x+1)+f(−1) f(x)=x^3 ⇒f^′ (x)=3x^2 ⇒f^′ (−1)=3 and f(−1)=−1 ⇒ y=3(x+1)−1 ⇒y=3x+2 18) { ((x−y+1=0 ⇒ { ((x−y=−1)),((7x+y=17)) :})),((7x+y=17)) :} Δ=8≠0 ⇒the systeme has one solution (a)

$$\left.\mathrm{1}\left.\mathrm{5}\right)\:{the}\:{corrct}\:{answer}\:{is}\:{a}\right) \\ $$$$\left.\mathrm{16}\right)\:{equation}\:{of}\:{tangente}\:{at}\:{x}=−\mathrm{1}\:{is}\:{y}={f}^{'} \left(−\mathrm{1}\right)\left({x}+\mathrm{1}\right)+{f}\left(−\mathrm{1}\right) \\ $$$${f}\left({x}\right)={x}^{\mathrm{3}} \:\Rightarrow{f}^{'} \left({x}\right)=\mathrm{3}{x}^{\mathrm{2}} \:\Rightarrow{f}^{'} \left(−\mathrm{1}\right)=\mathrm{3}\:{and}\:{f}\left(−\mathrm{1}\right)=−\mathrm{1}\:\Rightarrow \\ $$$${y}=\mathrm{3}\left({x}+\mathrm{1}\right)−\mathrm{1}\:\:\Rightarrow{y}=\mathrm{3}{x}+\mathrm{2} \\ $$$$\left.\mathrm{18}\right)\:\begin{cases}{{x}−{y}+\mathrm{1}=\mathrm{0}\:\Rightarrow\begin{cases}{{x}−{y}=−\mathrm{1}}\\{\mathrm{7}{x}+{y}=\mathrm{17}}\end{cases}}\\{\mathrm{7}{x}+{y}=\mathrm{17}}\end{cases} \\ $$$$\Delta=\mathrm{8}\neq\mathrm{0}\:\Rightarrow{the}\:{systeme}\:{has}\:{one}\:{solution}\:\:\:\left({a}\right) \\ $$

Answered by Rio Michael last updated on 17/Aug/19

15) A

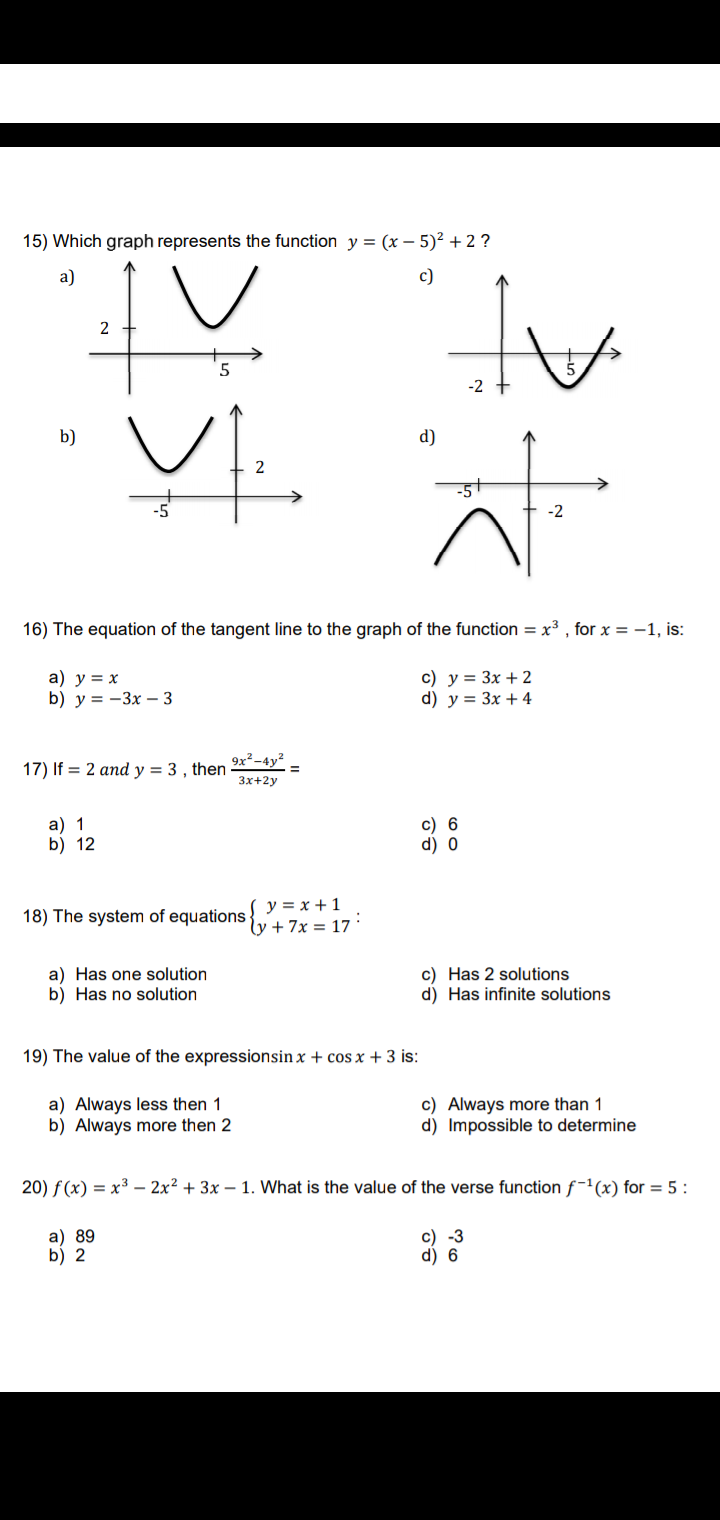
$$\left.\mathrm{15}\right)\:{A} \\ $$$$ \\ $$

Commented by aliesam last updated on 17/Aug/19

thank you sir

$${thank}\:{you}\:{sir} \\ $$

Answered by Tanmay chaudhury last updated on 17/Aug/19

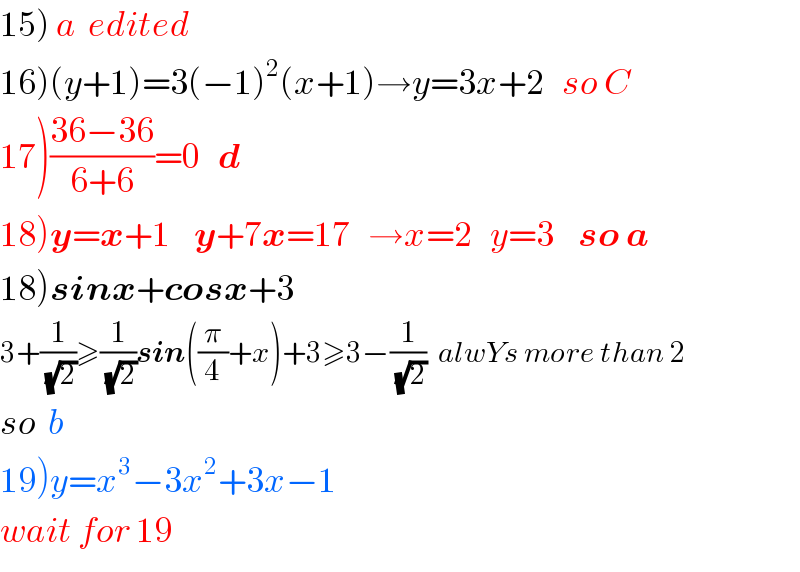
15) a edited 16)(y+1)=3(−1)^2 (x+1)→y=3x+2 so C 17)((36−36)/(6+6))=0 d 18)y=x+1 y+7x=17 →x=2 y=3 so a 18)sinx+cosx+3 3+(1/(√2))≥(1/(√2))sin((π/4)+x)+3≥3−(1/(√2)) alwYs more than 2 so b 19)y=x^3 −3x^2 +3x−1 wait for 19

$$\left.\mathrm{15}\right)\:{a}\:\:{edited} \\ $$$$\left.\mathrm{16}\right)\left({y}+\mathrm{1}\right)=\mathrm{3}\left(−\mathrm{1}\right)^{\mathrm{2}} \left({x}+\mathrm{1}\right)\rightarrow{y}=\mathrm{3}{x}+\mathrm{2}\:\:\:{so}\:{C} \\ $$$$\left.\mathrm{17}\right)\frac{\mathrm{36}−\mathrm{36}}{\mathrm{6}+\mathrm{6}}=\mathrm{0}\:\:\:\boldsymbol{{d}} \\ $$$$\left.\mathrm{18}\right)\boldsymbol{{y}}=\boldsymbol{{x}}+\mathrm{1}\:\:\:\:\boldsymbol{{y}}+\mathrm{7}\boldsymbol{{x}}=\mathrm{17}\:\:\:\rightarrow{x}=\mathrm{2}\:\:\:{y}=\mathrm{3}\:\:\:\:\boldsymbol{{so}}\:\boldsymbol{{a}} \\ $$$$\left.\mathrm{18}\right)\boldsymbol{{sinx}}+\boldsymbol{{cosx}}+\mathrm{3} \\ $$$$\mathrm{3}+\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\geqslant\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\boldsymbol{{sin}}\left(\frac{\pi}{\mathrm{4}}+{x}\right)+\mathrm{3}\geqslant\mathrm{3}−\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\:\:{alwYs}\:{more}\:{than}\:\mathrm{2} \\ $$$${so}\:\:{b} \\ $$$$\left.\mathrm{19}\right){y}={x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{1} \\ $$$${wait}\:{for}\:\mathrm{19} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com