
Question Number 65929 by Masumsiddiqui399@gmail.com last updated on 06/Aug/19
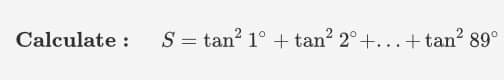
Commented by kaivan.ahmadi last updated on 06/Aug/19
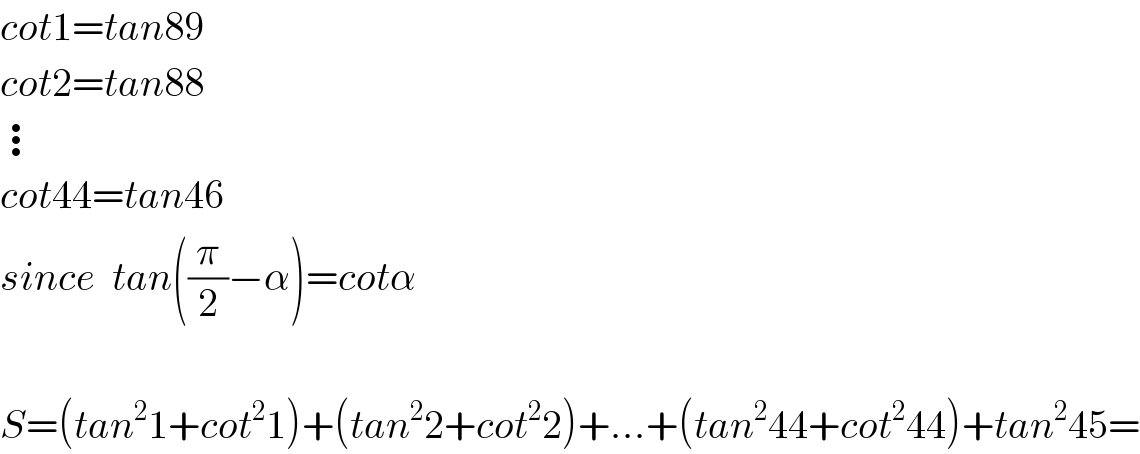
$${cot}\mathrm{1}={tan}\mathrm{89} \\ $$$${cot}\mathrm{2}={tan}\mathrm{88} \\ $$$$\vdots \\ $$$${cot}\mathrm{44}={tan}\mathrm{46} \\ $$$${since}\:\:{tan}\left(\frac{\pi}{\mathrm{2}}−\alpha\right)={cot}\alpha \\ $$$$ \\ $$$${S}=\left({tan}^{\mathrm{2}} \mathrm{1}+{cot}^{\mathrm{2}} \mathrm{1}\right)+\left({tan}^{\mathrm{2}} \mathrm{2}+{cot}^{\mathrm{2}} \mathrm{2}\right)+...+\left({tan}^{\mathrm{2}} \mathrm{44}+{cot}^{\mathrm{2}} \mathrm{44}\right)+{tan}^{\mathrm{2}} \mathrm{45}= \\ $$
Commented by Tony Lin last updated on 08/Aug/19

Answered by MJS last updated on 06/Aug/19

$$\frac{\mathrm{15931}}{\mathrm{3}}=\frac{\mathrm{89}×\mathrm{179}}{\mathrm{3}} \\ $$
