
Question Number 65581 by aliesam last updated on 31/Jul/19

Commented by mathmax by abdo last updated on 31/Jul/19
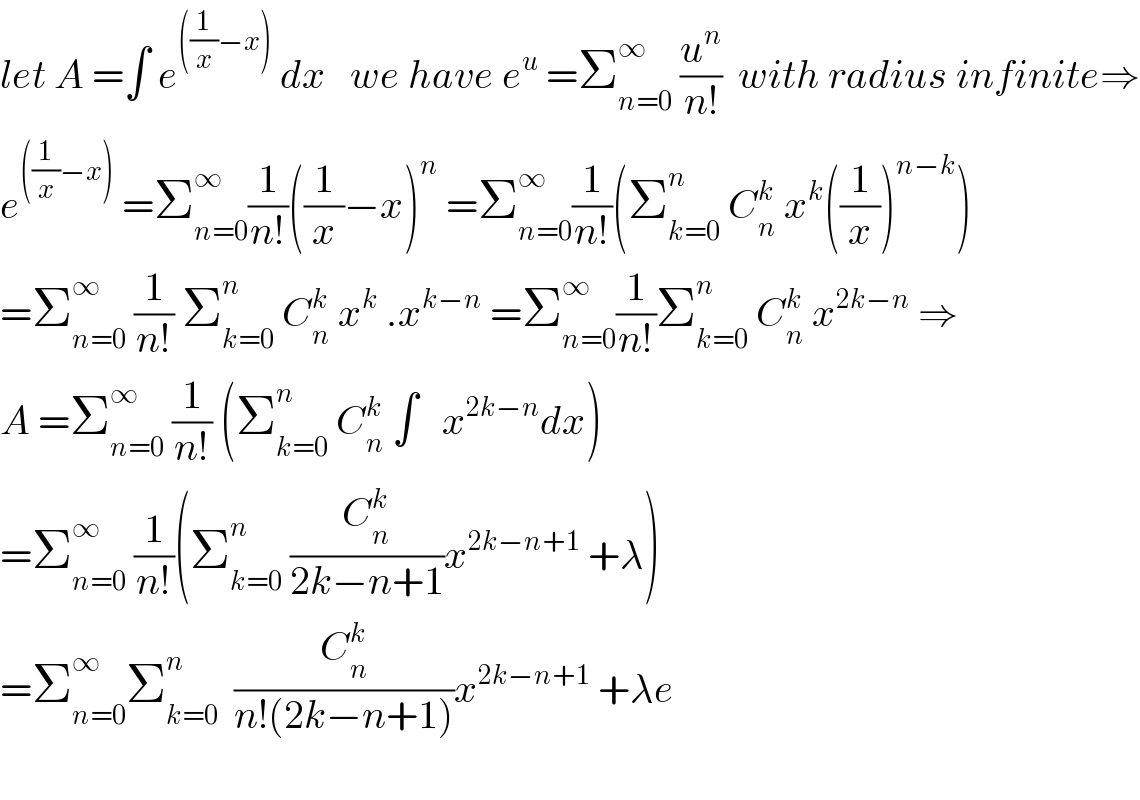
$${let}\:{A}\:=\int\:{e}^{\left(\frac{\mathrm{1}}{{x}}−{x}\right)} \:{dx}\:\:\:{we}\:{have}\:{e}^{{u}} \:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{u}^{{n}} }{{n}!}\:\:{with}\:{radius}\:{infinite}\Rightarrow \\ $$$${e}^{\left(\frac{\mathrm{1}}{{x}}−{x}\right)} \:=\sum_{{n}=\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{{n}!}\left(\frac{\mathrm{1}}{{x}}−{x}\right)^{{n}} \:=\sum_{{n}=\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{{n}!}\left(\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:{x}^{{k}} \left(\frac{\mathrm{1}}{{x}}\right)^{{n}−{k}} \right) \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{{n}!}\:\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:{x}^{{k}} \:.{x}^{{k}−{n}} \:=\sum_{{n}=\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{{n}!}\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:{x}^{\mathrm{2}{k}−{n}} \:\Rightarrow \\ $$$${A}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{{n}!}\:\left(\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:\int\:\:\:{x}^{\mathrm{2}{k}−{n}} {dx}\right) \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{{n}!}\left(\sum_{{k}=\mathrm{0}} ^{{n}} \:\frac{{C}_{{n}} ^{{k}} }{\mathrm{2}{k}−{n}+\mathrm{1}}{x}^{\mathrm{2}{k}−{n}+\mathrm{1}} \:+\lambda\right) \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \sum_{{k}=\mathrm{0}} ^{{n}} \:\:\frac{{C}_{{n}} ^{{k}} }{{n}!\left(\mathrm{2}{k}−{n}+\mathrm{1}\right)}{x}^{\mathrm{2}{k}−{n}+\mathrm{1}} \:+\lambda{e} \\ $$$$ \\ $$
